Project Evaluation and Selection for the Formation of the Optimal Portfolio
Developed by Roberto Hernandez Garcia
The increasing intensity of competition and fast technology changes have pushed firms to develop more innovative products. Generally, these are risky due to the uncertainty surrounding its technological feasibility and its future commercial success, which make their evaluation and selection difficult to achieve. This point is crucial, since the survival of an organization is highly correlated with correct project selection and management [1]. A wide diversity of approaches have been developed and used in order to cope with this problem, each of them with its own advantages and disadvantages. The most common (which from now on are referred as traditional methods) are quantitative, qualitative and hybrids methods [1].
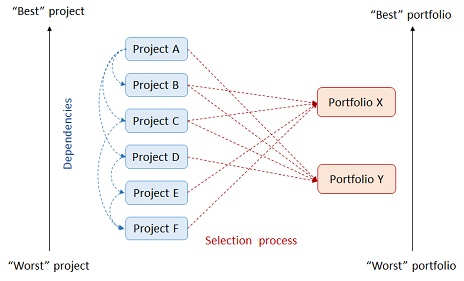
Even if the projects are correctly evaluated separately, this does not guarantee that the best portfolio can be formed. Figure 1 shows how the best portfolio may not include the best projects. The best portfolio is the one that maximizes the probabilities of achieving the goals set by the company [2]. Choosing the best projects based on any isolated criteria may not result in the best portfolio due to dependencies that may exist between the projects. The most common of them are related to cost, resources, outcomes, and impact [3]. These dependencies add complexity to the decision that needs to be taken, since the decision-making process becomes less straightforward.
If a company decides to evaluate a portfolio as it would evaluate projects, the amount of time required would be unmanageable. With only a set of 10 projects, the decision-maker would need to evaluate 1024 portfolios [4], which would be impossible for most of the companies. In consequence, newer methods, like Chien's Portfolio Evaluation Framework and Robust Portfolio Modeling, have been developed to assist with choosing the best portfolio within a shorter time.
This article focuses on describing and commenting about both traditional methods and the newer ones, in order to offer enough information for understanding their use, advantages and disadvantages. Their utilization and in-depth analysis does not form part of this article (for more information, consult the section Related Material).
Contents |
Background
Application Context
Resource allocation and project portfolio selection are focal decisions in public administration and industrial firms [5]. Every organization has a specific business strategy that facilitate reaching its long-term goals. In consequence, ideas and concepts are developed, and products and services are designed, developed, manufactured and sold. However, companies need to take decisions along this path, since they do not have unlimited resources for supporting every idea. Nevertheless, both benefits and risks are difficult to measure, since perfect information is almost never available. In part, risk management helps to handle part of the uncertainty; however, challenges will always exist.
According to the Project Management Institute, a portfolio is "a collection of projects and/or programs and other work that are grouped together to facilitate the effective management of that work to meet strategic business objectives. The components of a portfolio are quantifiable; that is, they can be measured, ranked, and prioritized" [6]. In that way, the optimal portfolio would be the one that, given a determined array of components, yields the maximum benefits and best meets the company's objectives.
Development History
The Project Management Institute (PMI) was founded in 1969 in the United States. This organism publishes the most common best practices in project and portfolio management.
Even though some standards and recommendations exist, few project selection models are being used by decision makers in practice. The number of selection models, along with users interest in applying them, grew exponentially in the 1950's and 1960's; however, this trend has reversed since the mid-1970's [2].
The current state of project and portfolio management development is quite different. In one hand, project management has been widely studied during the last decades, and few new methods, tools or techniques are still being developed; on the other hand, program and portfolio management are still under research, since one of their most important factors for success is technology development. A greater processing capacity in computers is fundamental in developing and using new software and models that allow a more efficient and faster portfolio management.
Acceptance and Use
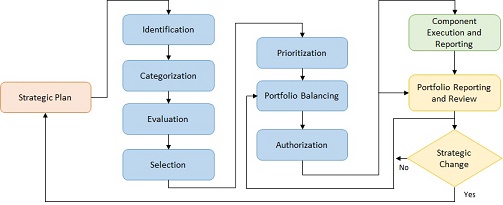
According to the PMI, the portfolio management process is a series of interrelated processes, as shown in Figure 2 [6]. This article focuses mainly on the Evaluation, Selection, Prioritization and Portfolio Balancing phases. The processes and tasks described in this sections have been recognized as good practices in the discipline of portfolio management-
The PMI defines the Evaluation phase as the process for gathering all relevant information to evaluate components (projects, tasks, etc.), with the purpose of comparing them, in order to facilitate the selection process. The recommended key activities for this process are:
- Evaluate each component with a scoring model with weighted criteria. The criteria may be related to business strategy, financial benefits, risk, legal/regulatory compliance, human resources, marketing and technical criteria (See The Standard for Portfolio Management for a complete list).
- Produce graphical representations (comparison grids, histograms, pie charts, line charts, and bubble diagrams) to facilitate decision-making.
- Make recommendations for a project, a category or the entire portfolio (expert judgement may be used for this activity).
Once the Evaluation phase has been completed, it is required to move to the Selection phase. There are two main outputs for this phase:
- A list of categorized, evaluated and selected components, which can be compared by category or for the entire portfolio.
- Recommendations list: can include prioritization, acceptance, or rejection of a component based on their analysis.
The most popular tools and techniques to ensure that the most desirable components are selected include human, financial and asset capacity analysis.
Next, the objective of the Prioritization phase is to generate a list of prioritized components within each strategic category. The most used tools are single and multiple weighted ranking, scoring techniques and expert judgement.
Finally, the Portfolio Balancing phase aims to develop the portfolio component mix with the greatest potential to both support the achievement of strategic objectives. The selection of the mix of components should also take into account similarities and synergies that exist between projects (dependencies). The most used tools, methods and techniques include cost benefit, quantitative, scenario, and probability analysis, as well as graphical analytical methods and expert judgement.
Following the recommendations for this part of the process, a decision-maker should be able to form the best portfolio. However, the PMI does not explain how to use most of the tools mentioned; nonetheless, a large number of articles and books regarding these topics have been available for some decades. Furthermore, even though it states that dependencies should be assessed, it does not explain how to do it, while it is not a topic as widely explored as the techniques and methods for evaluating, selecting and prioritizing individual projects.
From Project Evaluation and Selection to Balancing the Optimal Portfolio
In order to understand the process of the formation of the optimal portfolio, it is important to know the methods, tools and techniques that exists for the individual selection of projects, as well as the dependencies that influence project selection.
Traditional Methods for Project Evaluation & Selection
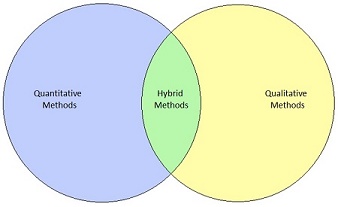
Three schools of thoughts have been identified [1] on how to classify the approaches for project portfolio evaluation and selection (Figure 3):
- Quantitative Methods: these approaches have been greatly developed since the early 1990's, but some of them have been around for more decades. However, they have been often criticized because of their focus on numerical information, even though tacit knowledge and qualitative information have also been considered relevant. Generally, they can be classified in six dimensions [7]:
- Benefit measurement methods: Five measures are particularly popular [8]: Net Present Value, Return on Investment, Cost-Benefit, Pay-Back Period and Pacifico and Sobelman Project Ratings.
- Mathematical programming approaches: linear, non-linear, integer, goal seek, dynamic, and stochastic programming, as well as fuzzy mathematical models.
- Simulation and heuristic models: Monte Carlo simulation, heuristic modeling and system dynamics simulations.
- Cognitive emulation approaches: decision-tree, game-theoretical approaches, statistical approaches and decision process analysis.
- Real options: approach that incorporates both uncertainty and the active decision making required for a strategy to succeed.
- Ad-hoc models: models built for specific purposes.
- Qualitative Methods: their focus is to take into account factors that quantitative methods cannot. Some of the most used are bubble diagrams, sensitivity analysis, benchmarking, check-lists, user centered design, group decision techniques and expert systems (all of them can be used by themselves, but it is also common to use them in combination with a quantitative method).
- Hybrid (Mixed) Methods: they are the most common methods for evaluating and selecting projects nowadays [8]. To qualify as a hybrid approach, the project evaluation and selection process has to contain a fairly balanced array of both classes of tools and techniques. Some good examples are graphical methods, conjoint analysis, data envelopment analysis and scenario planning.
Dependencies
The methods discussed in the previous section frequently do not lead to the formation of the optimal portfolio by themselves, since there are some factors that regularly are not taken into account. These factor are called interactions or dependencies, which have two main causes: internal and external factors. The former arises when the resource requirements and/or benefits of one project are affected by the selection (or rejection) of another project. On the other hand, the external interactions are those that arise over time from social and economic changes [9]. These dependencies may imply that two or more projects, when developed together, create synergies, while it can also be the case that they are mutually exclusive because of different reasons. Through this article, only the internal dependencies are going to be discusses, since the external ones are impossible to know/quantify beforehand by the decision-maker.
Some authors have identified different types of dependencies [2] [3] [10] , which can be summarized in 4 major sources: costs, resources, outcome, and impact dependencies. Some of them may overlap in scope, but are different in essence.
Cost Dependency
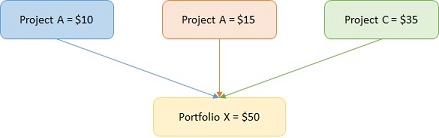
It is also called resource-utilization dependency. This dependency arises when the sum of the costs of two or more projects within a portfolio is not the same at the total cost of the entire portfolio (as displayed in Figure 4) due to some degree of resource sharing [3][9], e.g. a project may require using a new machine, but it is possible to share it with other projects or with ongoing operations.
Resources Dependency
This dependency is more related to the time that a certain project may require. Its root cause is the learning curve derived from the employees' experience. A good example is that of the reduction in development times of two similar products (probably the second one will require less time because of the experience acquired during the development of the first one).
Outcome Dependency
This interaction occurs when the probability of success of a given project depends on the outcome (success or failure) of one or more of the other projects [2][9]. The problem for the decision-maker arises when trying to translate this situation to numbers or comparable criteria. This type of dependencies are common in software or hardware development, like the case of a new printer that requires the development of a new technology for printing with twice the speed as the previous model. Obviously, the printer cannot be released to market if the printing technology has not been successfully developed.
Impact Dependency
An impact or benefit dependency may occur when the impacts of payoffs of the projects are not additive. In this case, projects may be said to be complementary or competitive, e.g. cannibalism. A good example is what happens when a company decides to introduce a new product to a specific market segment, successfully increasing the overall sales. At the same time, another project's objective is to add a special feature that will make it more attractive to another demographic group. If both projects are implemented, then the net total sales may be lower than the sum of the individual sales figure, since some original buyers may not consider it attractive anymore [9].
Methods for the Formation of the Optimal Portfolio
New methods have been developed during the last decade that go further in the evaluation and selection of projects for the formation of a better -optimal- portfolios. Their advantage over the traditional tools, methods and techniques is that they do consider dependencies.
Chien's Portfolio-Evaluation Framework
This framework guides the construction of measuring scales of the various portfolio attributes and facilitates trade-offs among them for the construction of the optimal portfolio. There are the three main phases involved:
- Identifying the portfolio objectives and selecting the associated portfolio attributes.
- Selecting or constructing scales for measuring portfolio attributes.
- Measuring the alternative portfolios by aggregating attributes.
These attributes, which are identified for the ideal or desired portfolio, should guide the decision-maker in order to reach the objectives of the company. In consequence, the attributes considered in portfolio formation would not be the same as the ones used for project selection. In order to choose the correct attributes, this framework proposes a new taxonomy of portfolio attributes:
- Independent portfolio attributes: those to which the contribution of each project is independent of other projects. Then, for obtaining an evaluating measure for the portfolio, the measure for each project should be linearly added together.
- Interrelated portfolio attributes: those to which the contribution of the projects are interrelated.
- Synergistic portfolio attributes: these are the holistic contribution of the selected projects, and can only be measured when considering preferences among alternative portfolios.
Robust Portfolio Modeling
Robust Portfolio Modeling (RPM) [10] was created in 2007 for determining an optimum project portfolio. Originally, RPM was a framework for project portfolio selection with independent projects and fixed budget; however, it was later extended by admitting a wide range of project dependencies, among other changes [5].
Under this framework, determined amounts of projects are evaluated with regard different criteria, assigning a score for every one of them. In consequence, a score matrix is created and an overall value for each project is obtained by taking into account weights depending on the importance of each criterion. As a result, a project is preferred to another if it has higher overall value. RPM establishes that a project portfolio is a subset of available projects, while the overall value of a portfolio is the sum of the overall value of its projects. In RPM, the possible portfolios should be defined by a set of linear inequalities. At the same time, the following types of constraints are considered and should be modeled:
- Budget constraints: include costs of the individual projects and the available total budget. In case of projects that deliver savings, then these are included as negative costs.
- Logical constraints: are used to model mutually exclusive and time-dependent projects, e.g. project B can only be included if project A is or has already been chosen.
- Positioning constraints: are in charge of ensuring alignment with the strategic requirements, e.g. a minimum number or projects is required for strategy X.
- Threshold constraints: ensure that the portfolio meets minimum requirements, like a determined payback period or utilizing all available workforce.
- Dependency constraints: are used to include any kind of dependency among projects. These can only be included as linear constraints with dummy projects.
This transformation and manipulation of constraints allows using linear programming. For further reading on examples and applicability of RPM, please refer to the Related Material section.
Related Material
For more in depth analysis and understanding of the portfolio management process, some standards are generally consulted. For example, the Standard for Portfolio Management, published by the PMI, goes deeply into the steps, tools and outcomes that every phase of the portfolio management process requires.
On the other hand, a case study is presented by Smith and Sonnenblick (2013) [11], where a pharmaceutical company, HealthPharma, faces the problem of project evaluation, selection, prioritization and portfolio management. The article shows different phases of portfolio management and the decisions that should be taken internally in order to construct a better portfolio with dependencies. This case study works as a good guideline in order to better understand the topics covered in this article.
Chien's Portfolio-Evaluation Framework [2] is explained in Chien's article through an example of the National Cancer Institute on the American Stop Smoking Intervention Study (consult the References section).
Finally, for a better understanding of Robust Portfolio Modeling consult RPM - Aalto University's webpage, which gives a more detailed explanation of this framework, and shows a list of both publications related to the model and the past and on-going research projects. Some of the applications has been observed on companies and government agencies like Nokia, Tekes, The Finnish Forest Industries Federations and the Finnish Defense Forces, among others.
Discussion
Strengths and weaknesses
The models presented in this article (both traditional and newer ones) have inherent strengths and weaknesses.
Traditional Methods
The strengths of the methods, tools and techniques for the traditional project evaluation and selection are:
- There has been a constant and vast research surrounding their use and application in case companies.
- Most of them are easy to understand and to explain, so communication and training within a company is facilitated.
- When combined, they cover both quantitative and qualitative aspects of projects.
- Different criteria can be used to evaluate and select taking into account different perspectives.
However, they do also have some important weaknesses [2]:
- The treatment given to evaluation criteria may not be appropriate, and this can be intensified by the presence of dependencies.
- There may be problems with handling non-monetary aspects.
- There is no recognition and incorporation of the experience and knowledge of the decision makers.
- Some managers have stated that they do not rely in these methods because, historically, they have not seen an improvement in the results of their choices.
- The go/kill decision points are generally weak and decisions are not taken in the right moment.
Models for the Formation of the Optimal Portfolio
On the other hand, the newer models previously presented for the formation of the optimal portfolio have some strengths that attack some of the traditional models' weaknesses:
- They take into account dependencies among projects.
- They can consider different criteria, even if they are interrelated.
- The experience of the decision makers is relevant for its proper utilization.
- Guarantees that the project mix is indeed the optimal one.
- Takes into account the strategy and other criteria at the same time.
Nevertheless, it has two main weaknesses that are quite evident:
- Their research and development is in course, so there are not as many articles and books that explain how they should be used.
- The level of sophistication is higher, so it may prevent people from using them.
- Even if the decision maker understands and correctly applies the method, communicating and explaining the results to other people may be a challenge.
However, investing time and resources in leaning how to use these techniques may lead to a better portfolio formation.
Relationship to other Material
Understanding these methods will eventually result in a better portfolio formation. However, this process should beforehand be aligned with the resource allocation process, since it is a basic constraint that limits the number of projects that a company can develop. At the same time, portfolio management have a very tight link to business strategy, since it is by this mean that the company accomplishes its objectives. In consequence, the portfolio management process is iterative, allowing and demanding for changes when the goals are achieved, so new projects and portfolio are formed in order to reach higher benefits, markets or reputation.
Implementation Advice
It should be noted that the methods discussed in this article vary on its degree of easiness of implementation. Some of them do not require any strong formal formation or education, nor having previous experience with similar tools. Quantitative methods, especially those related to financial indicators, are the most spread and used among industries for portfolio management and project selection [12] ; however, even these metrics are frequently not used in the right situations. Some recommendations for when and why using them are [13]:
- NPV: should be used to generate portfolios with long term and positive cash flow streams for companies in high growth industries.
- Internal Rate of Return and the Profitability Index: should be used to generate higher return on capital investment. It is recommended for companies competing in slow growth (but large revenue) industries, where capital efficiency is the key to success.
- Adjusted Payback Period: should be used to generate portfolios whose focus is on short term returns, which may be ideal for companies competing in shrinking industries.
In a similar way, every method, tool or technique commented throughout this article is better suited for specific situations, industries and objectives. It is imperative to understand when a certain technique is recommended and when a different approach should be used; however, boundaries are not always clear and the decision may be difficult to make, since most of the decision makers tend to stick with only a couple of methods.
References
- ↑ 1.0 1.1 1.2 Ashrafi, Maryam, Hamid Davoudpour, and Mohammad Abbassi. "Developing A Decision Support System For R&D Project Portfolio Selection With Interdependencies." AIP Conference Proceedings 1499.1 (2012): 370-378. Academic Search Premier.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Chien, C. "A Portfolio–Evaluation Framework For Selecting R&D Projects." R&D Management 32.4 (2002): 359-368. Business Source Premier.
- ↑ 3.0 3.1 3.2 Blau, Gary E., et al. "Managing A Portfolio Of Interdependent New Product Candidates In The Pharmaceutical Industry." Journal Of Product Innovation Management 21.4 (2004): 227-245. Business Source Premier.
- ↑ Ghapanchi, A.H. ( 1 ), et al. "A Methodology For Selecting Portfolios Of Projects With Interactions And Under Uncertainty." International Journal Of Project Management 30.7 (2012): 791-803. Scopus®.
- ↑ 5.0 5.1 Liesiö, J., P. Mild, and A. Salo. "Robust Portfolio Modeling With Incomplete Cost Information And Project Interdependencies." European Journal Of Operational Research 190.3 (2008): 679-695. Scopus®.
- ↑ 6.0 6.1 6.2 Project Management Institute, Inc. "The Standard for Portfolio Managements." (2006).
- ↑ Iamratanakul, S. ( 1 ), P. ( 2 ) Patanakul, and D. ( 3 ) Milosevic. "Project Portfolio Selection: From Past To Present." Proceedings Of The 4Th IEEE International Conference On Management Of Innovation And Technology, ICMIT Proceedings of the 4th IEEE International Conference on Management of Innovation and Technology, ICMIT (2008): 287-292. Scopus®.
- ↑ 8.0 8.1 Thamhain, Hans J. "Assessing The Effectiveness Of Quantitative And Qualitative Methods For R&D Project Proposal Evaluations." Engineering Management Journal 26.3 (2014): 3-12. Academic Search Premier.
- ↑ 9.0 9.1 9.2 9.3 Fox, G. Edward, Norman R. Baker, and John L. Bryant. "Economics Models For R And D Project Selection In The Presence Of Project Interactions." Management Science 30.7 (1984): 890-902. Business Source Premier.
- ↑ 10.0 10.1 Feyz, A. ( 1 ), and H. ( 2 ) Iranmanesh. "Using Robust Portfolio Modeling To Selecting Of New Product Development Projects: A Case Study." IEEM 2007: 2007 IEEE International Conference On Industrial Engineering And Engineering Management IEEM 2007: 2007 IEEE International Conference on Industrial Engineering and Engineering Management (2007): 979-983. Scopus®.
- ↑ Smith, Daniel, and Richard Sonnenblick. "From Budget-Based To Strategy-Based Portfolio Management. (Cover Story)." Research Technology Management 56.5 (2013): 45-51. Business Source Premier.
- ↑ Cooper, Robert, Scott Edgett, and Elko Kleinschmidt. "Portfolio Management For New Product Development: Results Of An Industry Practices Study." R&D Management 31.4 (2001): 361. Business Source Premier.
- ↑ Vitolo, Guilherme, and Flavio Cipparrone. "Strategic Implications Of Project Portfolio Selection." Accounting & Taxation 6.2 (2014): 11-20. Business Source Premier.