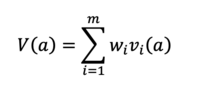Simple Multi-Attribute Rating Technique (SMART)
(→4: Numerical assessment of performance of each alternative on each criterion) |
(→Abstract) |
||
| (44 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
=Abstract= | =Abstract= | ||
| − | Simple Multi-Attribute Rating technique (SMART) is a method for conducting Multi-Criteria Decision Analysis (MCDA), in which assessment and selection of the best project alternative, amongst several different alternatives, is based on a list of relevant criteria. MCDA is a relatively new method for assessing alternatives or projects and it stems from the science of operations research. MCDA differs from traditional evaluations methods, like the cost-benefit-analysis (CBA), in multiple ways. Where a traditional CBA compares costs and benefits on a monetary scale, MCDA allows the assessment of alternatives on both a monetary as well as non-monetary scale. SMART is considered as one of the main techniques for MCDA and the overall purpose of SMART is generally to assist the decision maker when trying to choose the best option amongst several alternatives. SMART is based on a linear additive model, which means that a performance score for all individual alternatives can be calculated as the sum of the relative performance of each alternative on each identified evaluation criterion multiplied by the relative importance of that specific criterion. The technique therefore consist of three distinct elements: A set of alternatives, a set of criteria that the alternatives are to be evaluated on and the relative importance of these criteria, called the criteria weights. The best alternative is thus found by calculating a total performance score for each alternative and then selecting the one that reveals the highest total performance score. SMART provides a simple and intuitive method for supporting the decision maker. The method has become fairly popular in recent years and is used throughout many areas of application such as transportation and logistics, problem planning, project selection and manufacturing. SMART can be used as a supplement to other decision | + | Simple Multi-Attribute Rating technique (SMART) is a method for conducting Multi-Criteria Decision Analysis (MCDA), in which assessment and selection of the best project alternative, amongst several different alternatives, is based on a list of relevant criteria. MCDA is a relatively new method for assessing alternatives or projects and it stems from the science of operations research. MCDA differs from traditional evaluations methods, like the cost-benefit-analysis (CBA), in multiple ways. Where a traditional CBA compares costs and benefits on a monetary scale, MCDA allows the assessment of alternatives on both a monetary as well as non-monetary scale [1]. SMART is considered as one of the main techniques for MCDA and the overall purpose of SMART is generally to assist the decision maker when trying to choose the best option amongst several alternatives. SMART is based on a linear additive model, which means that a performance score for all individual alternatives can be calculated as the sum of the relative performance of each alternative on each identified evaluation criterion multiplied by the relative importance of that specific criterion. The technique therefore consist of three distinct elements: A set of alternatives, a set of criteria that the alternatives are to be evaluated on and the relative importance of these criteria, called the criteria weights. The best alternative is thus found by calculating a total performance score for each alternative and then selecting the one that reveals the highest total performance score. SMART provides a simple and intuitive method for supporting the decision maker [5]. The method has become fairly popular in recent years and is used throughout many areas of application such as transportation and logistics, problem planning, project selection and manufacturing. SMART can be used as a supplement to other decision tools, such as CBA. [2] |
=Big idea= | =Big idea= | ||
=== Background === | === Background === | ||
| − | Until now, one of the most common methodologies for assessing projects or conducting decision-making analysis, has been the traditional cost-benefit analysis (CBA). In the traditional CBA, the projects or alternatives are assessed using monetary calculations. This involves calculating the total net benefits of a project or alternative, based on the costs and benefits associated with that project or alternative, and then compare the achieved net benefits against the benefits of other projects. However, in recent years there has been a growing awareness of impacts that are difficult or even impossible to monetise and that these impacts are of importance and should be included in the decision-making process as well. Therefore, various decision-making methodologies has undergone changes in order to incorporate non-monetary aspects into the decision-making processes. Multi-Criteria Decision Analysis (MCDA) makes it possible to include both monetary and non-monetary aspect in the decision-making processes. Therefore, MCDA provides a tool for assessment or evaluation of different projects or alternatives, when both monetary and non-monetary aspects should be taken into account. | + | Until now, one of the most common methodologies for assessing projects or conducting decision-making analysis, has been the traditional cost-benefit analysis (CBA). In the traditional CBA, the projects or alternatives are assessed using monetary calculations. This involves calculating the total net benefits of a project or alternative, based on the costs and benefits associated with that project or alternative, and then compare the achieved net benefits against the benefits of other projects. However, in recent years there has been a growing awareness of impacts that are difficult or even impossible to monetise and that these impacts are of importance and should be included in the decision-making process as well. Therefore, various decision-making methodologies has undergone changes in order to incorporate non-monetary aspects into the decision-making processes. Multi-Criteria Decision Analysis (MCDA) makes it possible to include both monetary and non-monetary aspect in the decision-making processes. Therefore, MCDA provides a tool for assessment or evaluation of different projects or alternatives, when both monetary and non-monetary aspects should be taken into account [1]. |
=== What is MCDA? === | === What is MCDA? === | ||
==== The complex nature of decision problems and the use decision support ==== | ==== The complex nature of decision problems and the use decision support ==== | ||
| − | Often decision problems involve a large number of objectives and the decision maker might face more information than he can comprehend at once. The decision maker might therefore feel the need to simplify the problem considerable or to make use of various heuristics in order to make a decision. However, this might affect the quality of the decision. Decision analysis can be used to support the decision maker during the decision processes, when he is faced with multiple objectives. The idea behind decision support is to divide the problem into smaller and more tangible parts, analysing the smaller subproblems in detail and then recombining them into a final solution. By splitting the problems into smaller subproblems, the decision maker gains a deeper understanding of the overall problem. The main objective of the decision problem is to assist the decision maker during the decision process and to enable him/her to gain a deeper understanding of the decision problem. | + | Often decision problems involve a large number of objectives and the decision maker might face more information than he can comprehend at once. The decision maker might therefore feel the need to simplify the problem considerable or to make use of various heuristics in order to make a decision [6]. However, this might affect the quality of the decision [2]. Decision analysis can be used to support the decision maker during the decision processes, when he is faced with multiple objectives. The idea behind decision support is to divide the problem into smaller and more tangible parts, analysing the smaller subproblems in detail and then recombining them into a final solution. By splitting the problems into smaller subproblems, the decision maker gains a deeper understanding of the overall problem. The main objective of the decision problem is to assist the decision maker during the decision process and to enable him/her to gain a deeper understanding of the decision problem [3]. |
| − | MCDA is a relatively new approach for solving decision-making problems. The method tries to resolve some of the issues related to theoretical evaluation problems by taking an engineering approach, rather than an economics approach. The overall objective of MCDA is to allow the decision maker to break down complex decision problems into smaller and more tangible subproblems, which can be solved independently and then combined again. MCDA generally consist of a number of steps which breaks down the decision problem into three different components: (1) the alternatives, (2) the criteria for evaluating the performance of the alternatives and (3) the relative importance of the defined criteria. The identification of alternatives and the evaluation criteria constitute the objective part of the method, while the criteria weights for modelling the preference structure of the decision maker is considered the subjective part of the analysis. The purpose of MCDA is not to derive some optimal solution to a problem, but rather to assist the decision maker during an often complicated process of making decisions concerning multiple aspects. Some of the most recognised benefits associated with MCDA include helping the decision maker to understand the decision-making problem in further detail, improve the satisfaction of the decision process itself, improve the quality of the decision and to increase productivity during the decision-making process. There is a wide verity of MCDA tool, however one of the more common tools, which is the tool that this article will focus on, is the Simple Multi-Attribute Ranking Technique (SMART). | + | MCDA is a relatively new approach for solving decision-making problems. The method tries to resolve some of the issues related to theoretical evaluation problems by taking an engineering approach, rather than an economics approach [1]. The overall objective of MCDA is to allow the decision maker to break down complex decision problems into smaller and more tangible subproblems, which can be solved independently and then combined again. MCDA generally consist of a number of steps which breaks down the decision problem into three different components: (1) the alternatives, (2) the criteria for evaluating the performance of the alternatives and (3) the relative importance of the defined criteria. The identification of alternatives and the evaluation criteria constitute the objective part of the method, while the criteria weights for modelling the preference structure of the decision maker is considered the subjective part of the analysis. The purpose of MCDA is not to derive some optimal solution to a problem, but rather to assist the decision maker during an often complicated process of making decisions concerning multiple aspects. Some of the most recognised benefits associated with MCDA include helping the decision maker to understand the decision-making problem in further detail, improve the satisfaction of the decision process itself, improve the quality of the decision and to increase productivity during the decision-making process. There is a wide verity of MCDA tool, however one of the more common tools, which is the tool that this article will focus on, is the Simple Multi-Attribute Ranking Technique (SMART) [4]. |
=== What is SMART? === | === What is SMART? === | ||
| Line 26: | Line 26: | ||
=Application= | =Application= | ||
==1: Identify the decision maker== | ==1: Identify the decision maker== | ||
| − | The first stage out of the eight stages involves the identification of the decision-maker. This stage is relatively straight forward in most cases, however it is important to have identified the person responsible for the decision making as it is his/her preferences that will reflect the outcome of the analysis. | + | The first stage out of the eight stages involves the identification of the decision-maker. This stage is relatively straight forward in most cases, however it is important to have identified the person responsible for the decision making as it is his/her preferences that will reflect the outcome of the analysis [3]. |
== 2: Identification of alternatives== | == 2: Identification of alternatives== | ||
| − | This stage concerns the identification of the different alternatives or projects to be chosen among. This could for instance be different infrastructure projects or alternative office locations. Like stage 1, this stage is also relatively straight forward. However, the alternatives chosen for the analysis should still be chosen with care. | + | This stage concerns the identification of the different alternatives or projects to be chosen among. This could for instance be different infrastructure projects or alternative office locations. Like stage 1, this stage is also relatively straight forward. However, the alternatives chosen for the analysis should still be chosen with care [2]. |
== 3: Identification of relevant evaluation criteria== | == 3: Identification of relevant evaluation criteria== | ||
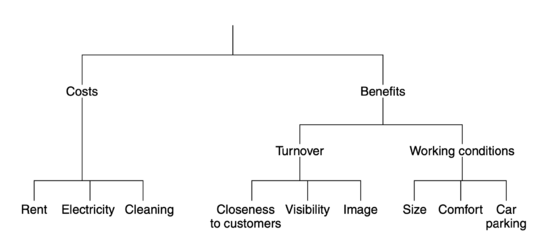
| − | We need criteria in order to assess the performance of each of the alternatives that was defined in stage 2. The criteria are used to measure the performance of an alternative in terms of the overall objective of the decision maker. If the overall objective of the decision maker was to choose the infrastructure project that return the largest socio-economic benefits, then the criteria should be defined so that they make it possible to assess each alternative according to this objective. If the overall objective was to find the best possible office location for a company, then we would have to define a set of criteria that makes it possible to assess the different office alternatives. These criteria could be rent, closeness to customer, size etc. The important part of defining the criteria is they need to be assessed on a numeric scale. Often it is helpful to construct a value tree and break down the overall criteria into smaller parts that can be assessed more easily. | + | We need criteria in order to assess the performance of each of the alternatives that was defined in stage 2. The criteria are used to measure the performance of an alternative in terms of the overall objective of the decision maker. If the overall objective of the decision maker was to choose the infrastructure project that return the largest socio-economic benefits, then the criteria should be defined so that they make it possible to assess each alternative according to this objective. If the overall objective was to find the best possible office location for a company, then we would have to define a set of criteria that makes it possible to assess the different office alternatives. These criteria could be rent, closeness to customer, size etc. The important part of defining the criteria is they need to be assessed on a numeric scale. Often it is helpful to construct a value tree and break down the overall criteria into smaller parts that can be assessed more easily [2]. |
[[File:ValueTree.png|center|thumb|550px|Figure 1: Example of a value tree when defining criteria for selection of a new office location.]] | [[File:ValueTree.png|center|thumb|550px|Figure 1: Example of a value tree when defining criteria for selection of a new office location.]] | ||
| − | When the criteria have been broken down to a lower level, they are much easier to assess. Figure 1 depicts a value tre where | + | When the criteria have been broken down to a lower level, they are much easier to assess. Figure 1 depicts a value tre where nine different criteria have been identified. The value tree should be constructed according to a number of rules: |
*'''Completeness:''' The tree should be complete which means that all relevant criteria for assessing the alternatives should be included at the bottom of the tree. | *'''Completeness:''' The tree should be complete which means that all relevant criteria for assessing the alternatives should be included at the bottom of the tree. | ||
| Line 46: | Line 46: | ||
==4: Numerical assessment of performance of each alternative on each criterion== | ==4: Numerical assessment of performance of each alternative on each criterion== | ||
| − | Now that the evaluation criteria have been defined, the decision maker must evaluate the performance of each alternative on these criteria. The first step is to identify variables to identify the criteria. For instance, the criteria "Size" from the office example depicted in figure 1 can be represented by the variable square meters. When these variables have been defined, one should see which variables that are quantifiable and which variables that are not quantifiable. | + | Now that the evaluation criteria have been defined, the decision maker must evaluate the performance of each alternative on these criteria. The first step is to identify variables to identify the criteria. For instance, the criteria "Size" from the office example depicted in figure 1 can be represented by the variable square meters. When these variables have been defined, one should see which variables that are quantifiable and which variables that are not quantifiable. If the variables representing the criteria are quantifiable, values functions can be used to derive the benefits of the alternatives. Another approach is called direct rating, and this can be used for both quantifiable and not quantifiable variables [1]. |
| + | |||
| + | ==== Direct rating ==== | ||
| + | In direct rating, the decision maker is asked to rank the alternatives from most preferred to least preferred. The alternative that is the most preferred one received a.score of 100. The alternative that is least preferred received a score of 0. The rest of the alternatives are given scores between 0 and 100 that represents the relative improvement when moving from one alternative to another. When each of the alternatives have been evaluated on the first criteria, then the process is repeated for the other criteria [1]. | ||
| + | |||
| + | ==== Value functions ==== | ||
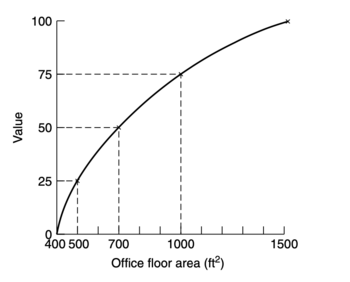
| + | When the variables representing the can easily be quantified. value functions can be used instead. Here the most preferred alternative, assesses on of the criteria, is given the value 100 and the least preferred alternative is given the value 0. Using a method called bisection, it is possible to achieve five points, namely the minimum (0), the 25th percentile, the 50th percentile, the 75th percentile and the 100th percentile. This makes it possible to plot the function and the scores for each alternative can be approximated. This procedure is then repeated for the rest of the quantifiable criteria, once again evaluating each alternative and assigning the scores according to their performance. Figure 2 below show a value function for the office location example. | ||
| + | |||
| + | [[File:ValueFunction.png|center|thumb|350px|Figure 1: Example of a value function for the office location example when evaluating the performance of each alternative on the criteria "Size".]] | ||
| + | |||
| + | When the performance of each alternative has been evaluated on each criteria, it is time to assign the importance of each criteria using criteria weights. | ||
==5: Assignment of relative importance weights for each of the evaluation criterion== | ==5: Assignment of relative importance weights for each of the evaluation criterion== | ||
| + | The importance of each criteria has to be described in accordance with the preferences of the decision maker. This is, as previously described, the subjective part of the appraisal process. The weights are assigned to the criteria using swing weights. These weights are derived by considering each of the criteria from the bottom of the decision tree. A fictive alternative is set up that performs worst on all criteria. The decision maker is then asked which criteria he would choose the fictive alternative to perform at maximum capacity on. Then he is asked which criteria he would then choose and so on. This is done until all criteria have been ranked according to their relative importance to the decision maker. The highest ranked criteria is given a weight of 100 and the other criteria are are assigned weights according to how important the decision maker think they are compared to the highest ranked criteria. After this is done, it is conventional to normalise the assigned weights, since this makes it easier to interpret their relative importance. | ||
==6: Calculation of a weighted average of the values that is assigned each of the alternatives== | ==6: Calculation of a weighted average of the values that is assigned each of the alternatives== | ||
| + | Now that the alternatives have been defined, the evaluation criteria have been identified, the performance of each alternative on each criteria is evaluated and now that the importance of the criteria are assigned each of the criteria, the total performance of each alternative can be calculated. As previously mentioned, SMART is an additive model and the total performance is calculated a weighted average of the performance of each alternative evaluated on each weighted criteria. Or written differently: | ||
| + | |||
| + | [[File:ValCal.png|center|thumb|200px|]] | ||
| + | |||
| + | The additive model is easy to understand and is one of the most frequently used models. However, the model has certain limitations, which will be described later on. | ||
==7: Making a provisional decision based on calculated performance scores== | ==7: Making a provisional decision based on calculated performance scores== | ||
| + | When the total performance has been calculated for all the alternatives, a provisional decision can be made. Here the performance of the different alternatives can be compared against one another and maybe adjustments to the model can be made if necessary [2]. | ||
==8: Sensitivity analysis and final decision== | ==8: Sensitivity analysis and final decision== | ||
| + | Sensitivity analysis is importance in order to check the robustness of the obtained solution. Robustness of a solution describes how sensitive the solution is to minor changes of the decision variables, such as the weights assigned for each of the criteria. If the model proves to be relatively robust against changes made to some of the parameters, a conclusion might be drawn. However, if the solution differes from minor adjustments to some of the model parameters, a revision is necessary before any conclusion can be drawn [1]. | ||
=Limitations= | =Limitations= | ||
| − | + | === Axioms === | |
| + | This section concerns some of the limitations of SMART and MCDA as well as the application area. First of all, it is important to state that SMART makes use of a set of axioms and assumptions considering the preferences of the decision maker. The first axiom states that it is assumed that the decision maker is able to decide between two options, given he prefers one more than the other. This axiom is called decidability and concerns the decision maker's ability to make a decision between the alternatives. The next axiom is called transitivity. This states that if A is preferred to B and B is preferred to C, then A must be preferred to C as well. The third axiom is summation and it implies that if the decision maker prefers A over B and he prefers B over C, then the strength of preference for A over C is larger than that of A over B. The forth axiom is solvability and it concerns the measure of improvements in regard to the value functions. The fifth axiom is that there should be finite upper and lower bounds for the values assigned the alternatives [2]. Besides this, mutual preference independence is assumed to exist between the defined evaluation criteria [1]. | ||
| + | |||
| + | === Cons of SMART === | ||
| + | The assessment of value functions when evaluating the performance of alternatives over the criteria or the assignment of swing weights can be difficult in practice. This can result in an inaccurate model for the decision support or a model that does not correctly reflect the preferences of the decision maker. A general concern of MCDA, and not just SMART, is that the method cannot provide the decision maker with a definitive solution. The tool should bee seen as support for the decision making rather than a model teaching for a hidden truth. SMART is also quite a time and resource intensive, which can be frustrating. Besides this, there might arise multiple problems when assigning the evaluation criteria their weights and the decision maker should be aware that his or her elicitation of importance weights can change the solution significantly. Finally, it should be noted that the additive model has certain limitations and this means that SMART is not suitable for all decision problems. The model is not suitable when there is dependencies or interactions between the weights of some of the criteria [2]. | ||
=Annotated bibliography= | =Annotated bibliography= | ||
| − | + | # ''Decision Support And Strategic Assessment'' is chosen as the one of the writings for this article. This is because I've previously used the compendium for decision making. This text mainly considers decision making in regard to infrastructure project. However, the methods described are also applicable to most other decision making problems. | |
| + | # ''Decision Analysis for Management Judgement'' is chosen since this literature very throughly goes through each of the previously described stages of the SMART tool. The text also makes use of examples which makes it easy to understand when and how SMART is to be applied. | ||
| + | # ''SMART - Multi-criteria decision-making technique for use in planning activities" describes the use of SMART using an example where the decision maker needs to dispose waste material. The article is well written and describes some of the limitations of SMART. | ||
| + | # ''SUPPORTING SUSTAINABLE TRANSPORT APPRAISALS USING STAKEHOLDER INVOLVEMENT AND MCDA'' describes how MCDA, including SMART, can be used for assessment of projects. | ||
| − | DTU | + | =References= |
| + | # ''Decision Support And Strategic Assessment'', DTU Management Compendium, Michael Bruhn Barfod and Steen Leleur, 2019 | ||
| + | # ''Decision Analysis for Management Judgement'', John Wiley & Sons, Paul Goodwin and George Wright, Third Edition, 2004 | ||
| + | # ''SMART - Multi-criteria decision-making technique for use in planning activities'', M. Patel, M. Vashi and B. Bhatt, Sarvajanik College of Engineering and Technology, 2017 | ||
| + | # ''SUPPORTING SUSTAINABLE TRANSPORT APPRAISALS USING STAKEHOLDER INVOLVEMENT AND MCDA'', DTU, Michael Bruhn Barfod, 2018 | ||
| + | # ''Giving current and future generations a real voice: a practical method for constructing sustainability viewpoints in transport appraisal'', EJTIR, Y. Cornet and M. Barfoed et al., 2018 | ||
| + | # ''SMARTS and SMARTER: Improved Simple Methods for Multiattribute Utility Measurement Organizational Behavior and Human Decision Processes'',Edwards, W. and Barron, Elsevier | ||
Latest revision as of 22:40, 28 February 2021
[edit] Abstract
Simple Multi-Attribute Rating technique (SMART) is a method for conducting Multi-Criteria Decision Analysis (MCDA), in which assessment and selection of the best project alternative, amongst several different alternatives, is based on a list of relevant criteria. MCDA is a relatively new method for assessing alternatives or projects and it stems from the science of operations research. MCDA differs from traditional evaluations methods, like the cost-benefit-analysis (CBA), in multiple ways. Where a traditional CBA compares costs and benefits on a monetary scale, MCDA allows the assessment of alternatives on both a monetary as well as non-monetary scale [1]. SMART is considered as one of the main techniques for MCDA and the overall purpose of SMART is generally to assist the decision maker when trying to choose the best option amongst several alternatives. SMART is based on a linear additive model, which means that a performance score for all individual alternatives can be calculated as the sum of the relative performance of each alternative on each identified evaluation criterion multiplied by the relative importance of that specific criterion. The technique therefore consist of three distinct elements: A set of alternatives, a set of criteria that the alternatives are to be evaluated on and the relative importance of these criteria, called the criteria weights. The best alternative is thus found by calculating a total performance score for each alternative and then selecting the one that reveals the highest total performance score. SMART provides a simple and intuitive method for supporting the decision maker [5]. The method has become fairly popular in recent years and is used throughout many areas of application such as transportation and logistics, problem planning, project selection and manufacturing. SMART can be used as a supplement to other decision tools, such as CBA. [2]
[edit] Big idea
[edit] Background
Until now, one of the most common methodologies for assessing projects or conducting decision-making analysis, has been the traditional cost-benefit analysis (CBA). In the traditional CBA, the projects or alternatives are assessed using monetary calculations. This involves calculating the total net benefits of a project or alternative, based on the costs and benefits associated with that project or alternative, and then compare the achieved net benefits against the benefits of other projects. However, in recent years there has been a growing awareness of impacts that are difficult or even impossible to monetise and that these impacts are of importance and should be included in the decision-making process as well. Therefore, various decision-making methodologies has undergone changes in order to incorporate non-monetary aspects into the decision-making processes. Multi-Criteria Decision Analysis (MCDA) makes it possible to include both monetary and non-monetary aspect in the decision-making processes. Therefore, MCDA provides a tool for assessment or evaluation of different projects or alternatives, when both monetary and non-monetary aspects should be taken into account [1].
[edit] What is MCDA?
[edit] The complex nature of decision problems and the use decision support
Often decision problems involve a large number of objectives and the decision maker might face more information than he can comprehend at once. The decision maker might therefore feel the need to simplify the problem considerable or to make use of various heuristics in order to make a decision [6]. However, this might affect the quality of the decision [2]. Decision analysis can be used to support the decision maker during the decision processes, when he is faced with multiple objectives. The idea behind decision support is to divide the problem into smaller and more tangible parts, analysing the smaller subproblems in detail and then recombining them into a final solution. By splitting the problems into smaller subproblems, the decision maker gains a deeper understanding of the overall problem. The main objective of the decision problem is to assist the decision maker during the decision process and to enable him/her to gain a deeper understanding of the decision problem [3].
MCDA is a relatively new approach for solving decision-making problems. The method tries to resolve some of the issues related to theoretical evaluation problems by taking an engineering approach, rather than an economics approach [1]. The overall objective of MCDA is to allow the decision maker to break down complex decision problems into smaller and more tangible subproblems, which can be solved independently and then combined again. MCDA generally consist of a number of steps which breaks down the decision problem into three different components: (1) the alternatives, (2) the criteria for evaluating the performance of the alternatives and (3) the relative importance of the defined criteria. The identification of alternatives and the evaluation criteria constitute the objective part of the method, while the criteria weights for modelling the preference structure of the decision maker is considered the subjective part of the analysis. The purpose of MCDA is not to derive some optimal solution to a problem, but rather to assist the decision maker during an often complicated process of making decisions concerning multiple aspects. Some of the most recognised benefits associated with MCDA include helping the decision maker to understand the decision-making problem in further detail, improve the satisfaction of the decision process itself, improve the quality of the decision and to increase productivity during the decision-making process. There is a wide verity of MCDA tool, however one of the more common tools, which is the tool that this article will focus on, is the Simple Multi-Attribute Ranking Technique (SMART) [4].
[edit] What is SMART?
SMART is a MCDA analysis tool based on a linear additive model. The tool was first introduced by Edwards in 1971 and has since then gained a lot of attention because of its transparent approach compared to many other assessment tool, such as CBA. Because the tool asks the decision maker to reveal his or her preferences, SMART makes it possible to gain a deeper understanding of the decision problem. SMART can be applied in many different decision making applications and the method generally consist of eight stages. It is important to understand that the decision process often is iterative and the decision maker might go back and fourth the different stages. The eight stages are:
- 1) Identification of the decision maker: The person responsible for conducting the decision analysis must be known from the vary beginning of the analysis.
- 2) Identification of alternatives: The different courses of action or set of projects/alternatives should be identified.
- 3) Identification of relevant evaluation criteria: The criteria relevant to the decision problem should be identified, so that each of the alternatives defined in stage 2 can be assesses.
- 4) Numerical assessment of the performance of each alternative on each criterion: For each of the identified criteria, values for the performance of each alternative on that criteria is to be calculated.
- 5) Assignment of importance weights for each of the evaluation criteria: Each criterion must be assigned with a weighting that reflects its relative importance to the decision maker.
- 6) Calculation of a weighted average of the values that is assigned each of the alternatives: These calculations makes it possible to measure how well one alternative performs in comparison to the other alternatives, when performance is measured across all the defined criteria.
- 7) Provisional decision: On this stage the results obtained on stage 6 are interpreted. However, it should be noted that a final decision should not be drawn before the robustness of the solutions have been analysed in further detail.
- 8) Sensitivity analysis: Sensitivity analysis is carried out in order to see how robust the solution is in terms of small changes.
Each of these eight stages will be described in much further detain in the following sub-sections.
[edit] Application
[edit] 1: Identify the decision maker
The first stage out of the eight stages involves the identification of the decision-maker. This stage is relatively straight forward in most cases, however it is important to have identified the person responsible for the decision making as it is his/her preferences that will reflect the outcome of the analysis [3].
[edit] 2: Identification of alternatives
This stage concerns the identification of the different alternatives or projects to be chosen among. This could for instance be different infrastructure projects or alternative office locations. Like stage 1, this stage is also relatively straight forward. However, the alternatives chosen for the analysis should still be chosen with care [2].
[edit] 3: Identification of relevant evaluation criteria
We need criteria in order to assess the performance of each of the alternatives that was defined in stage 2. The criteria are used to measure the performance of an alternative in terms of the overall objective of the decision maker. If the overall objective of the decision maker was to choose the infrastructure project that return the largest socio-economic benefits, then the criteria should be defined so that they make it possible to assess each alternative according to this objective. If the overall objective was to find the best possible office location for a company, then we would have to define a set of criteria that makes it possible to assess the different office alternatives. These criteria could be rent, closeness to customer, size etc. The important part of defining the criteria is they need to be assessed on a numeric scale. Often it is helpful to construct a value tree and break down the overall criteria into smaller parts that can be assessed more easily [2].
When the criteria have been broken down to a lower level, they are much easier to assess. Figure 1 depicts a value tre where nine different criteria have been identified. The value tree should be constructed according to a number of rules:
- Completeness: The tree should be complete which means that all relevant criteria for assessing the alternatives should be included at the bottom of the tree.
- Operationality: All the bottom criteria in the tree are specified well enough, so the the decision maker can compare the alternatives when assessing their performance on the criteria.
- Decomposability: It is required that the performance of an alternative can be assessed independently of its performance on the other defined criteria.
- No redundancy: None of the criteria should duplicate each other in regard to what they represent.
- Minimum size: The value tree should be kept as small and simple as possible while still including the relevant criteria.
The next stage involves the assessment of the performance of each alternative on the defined evaluation criteria.
[edit] 4: Numerical assessment of performance of each alternative on each criterion
Now that the evaluation criteria have been defined, the decision maker must evaluate the performance of each alternative on these criteria. The first step is to identify variables to identify the criteria. For instance, the criteria "Size" from the office example depicted in figure 1 can be represented by the variable square meters. When these variables have been defined, one should see which variables that are quantifiable and which variables that are not quantifiable. If the variables representing the criteria are quantifiable, values functions can be used to derive the benefits of the alternatives. Another approach is called direct rating, and this can be used for both quantifiable and not quantifiable variables [1].
[edit] Direct rating
In direct rating, the decision maker is asked to rank the alternatives from most preferred to least preferred. The alternative that is the most preferred one received a.score of 100. The alternative that is least preferred received a score of 0. The rest of the alternatives are given scores between 0 and 100 that represents the relative improvement when moving from one alternative to another. When each of the alternatives have been evaluated on the first criteria, then the process is repeated for the other criteria [1].
[edit] Value functions
When the variables representing the can easily be quantified. value functions can be used instead. Here the most preferred alternative, assesses on of the criteria, is given the value 100 and the least preferred alternative is given the value 0. Using a method called bisection, it is possible to achieve five points, namely the minimum (0), the 25th percentile, the 50th percentile, the 75th percentile and the 100th percentile. This makes it possible to plot the function and the scores for each alternative can be approximated. This procedure is then repeated for the rest of the quantifiable criteria, once again evaluating each alternative and assigning the scores according to their performance. Figure 2 below show a value function for the office location example.
When the performance of each alternative has been evaluated on each criteria, it is time to assign the importance of each criteria using criteria weights.
[edit] 5: Assignment of relative importance weights for each of the evaluation criterion
The importance of each criteria has to be described in accordance with the preferences of the decision maker. This is, as previously described, the subjective part of the appraisal process. The weights are assigned to the criteria using swing weights. These weights are derived by considering each of the criteria from the bottom of the decision tree. A fictive alternative is set up that performs worst on all criteria. The decision maker is then asked which criteria he would choose the fictive alternative to perform at maximum capacity on. Then he is asked which criteria he would then choose and so on. This is done until all criteria have been ranked according to their relative importance to the decision maker. The highest ranked criteria is given a weight of 100 and the other criteria are are assigned weights according to how important the decision maker think they are compared to the highest ranked criteria. After this is done, it is conventional to normalise the assigned weights, since this makes it easier to interpret their relative importance.
[edit] 6: Calculation of a weighted average of the values that is assigned each of the alternatives
Now that the alternatives have been defined, the evaluation criteria have been identified, the performance of each alternative on each criteria is evaluated and now that the importance of the criteria are assigned each of the criteria, the total performance of each alternative can be calculated. As previously mentioned, SMART is an additive model and the total performance is calculated a weighted average of the performance of each alternative evaluated on each weighted criteria. Or written differently:
The additive model is easy to understand and is one of the most frequently used models. However, the model has certain limitations, which will be described later on.
[edit] 7: Making a provisional decision based on calculated performance scores
When the total performance has been calculated for all the alternatives, a provisional decision can be made. Here the performance of the different alternatives can be compared against one another and maybe adjustments to the model can be made if necessary [2].
[edit] 8: Sensitivity analysis and final decision
Sensitivity analysis is importance in order to check the robustness of the obtained solution. Robustness of a solution describes how sensitive the solution is to minor changes of the decision variables, such as the weights assigned for each of the criteria. If the model proves to be relatively robust against changes made to some of the parameters, a conclusion might be drawn. However, if the solution differes from minor adjustments to some of the model parameters, a revision is necessary before any conclusion can be drawn [1].
[edit] Limitations
[edit] Axioms
This section concerns some of the limitations of SMART and MCDA as well as the application area. First of all, it is important to state that SMART makes use of a set of axioms and assumptions considering the preferences of the decision maker. The first axiom states that it is assumed that the decision maker is able to decide between two options, given he prefers one more than the other. This axiom is called decidability and concerns the decision maker's ability to make a decision between the alternatives. The next axiom is called transitivity. This states that if A is preferred to B and B is preferred to C, then A must be preferred to C as well. The third axiom is summation and it implies that if the decision maker prefers A over B and he prefers B over C, then the strength of preference for A over C is larger than that of A over B. The forth axiom is solvability and it concerns the measure of improvements in regard to the value functions. The fifth axiom is that there should be finite upper and lower bounds for the values assigned the alternatives [2]. Besides this, mutual preference independence is assumed to exist between the defined evaluation criteria [1].
[edit] Cons of SMART
The assessment of value functions when evaluating the performance of alternatives over the criteria or the assignment of swing weights can be difficult in practice. This can result in an inaccurate model for the decision support or a model that does not correctly reflect the preferences of the decision maker. A general concern of MCDA, and not just SMART, is that the method cannot provide the decision maker with a definitive solution. The tool should bee seen as support for the decision making rather than a model teaching for a hidden truth. SMART is also quite a time and resource intensive, which can be frustrating. Besides this, there might arise multiple problems when assigning the evaluation criteria their weights and the decision maker should be aware that his or her elicitation of importance weights can change the solution significantly. Finally, it should be noted that the additive model has certain limitations and this means that SMART is not suitable for all decision problems. The model is not suitable when there is dependencies or interactions between the weights of some of the criteria [2].
[edit] Annotated bibliography
- Decision Support And Strategic Assessment is chosen as the one of the writings for this article. This is because I've previously used the compendium for decision making. This text mainly considers decision making in regard to infrastructure project. However, the methods described are also applicable to most other decision making problems.
- Decision Analysis for Management Judgement is chosen since this literature very throughly goes through each of the previously described stages of the SMART tool. The text also makes use of examples which makes it easy to understand when and how SMART is to be applied.
- SMART - Multi-criteria decision-making technique for use in planning activities" describes the use of SMART using an example where the decision maker needs to dispose waste material. The article is well written and describes some of the limitations of SMART.
- SUPPORTING SUSTAINABLE TRANSPORT APPRAISALS USING STAKEHOLDER INVOLVEMENT AND MCDA describes how MCDA, including SMART, can be used for assessment of projects.
[edit] References
- Decision Support And Strategic Assessment, DTU Management Compendium, Michael Bruhn Barfod and Steen Leleur, 2019
- Decision Analysis for Management Judgement, John Wiley & Sons, Paul Goodwin and George Wright, Third Edition, 2004
- SMART - Multi-criteria decision-making technique for use in planning activities, M. Patel, M. Vashi and B. Bhatt, Sarvajanik College of Engineering and Technology, 2017
- SUPPORTING SUSTAINABLE TRANSPORT APPRAISALS USING STAKEHOLDER INVOLVEMENT AND MCDA, DTU, Michael Bruhn Barfod, 2018
- Giving current and future generations a real voice: a practical method for constructing sustainability viewpoints in transport appraisal, EJTIR, Y. Cornet and M. Barfoed et al., 2018
- SMARTS and SMARTER: Improved Simple Methods for Multiattribute Utility Measurement Organizational Behavior and Human Decision Processes,Edwards, W. and Barron, Elsevier