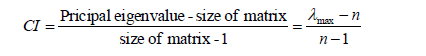MCDA methods in decision making
(→The Analytical Hierarchy Process (AHP)) |
(→The Analytical Hierarchy Process (AHP)) |
||
| (37 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
==Abstract== | ==Abstract== | ||
| − | Decision making is one of the most important parts of any aspect of life. It affects the present and both immediate and long-term future. Of course, it has a huge impact on every project, naturally including engineering projects. There is a vast number of techniques and methods to help one to come up with a final decision. In this article, the focus is the MCDA analysis in decision | + | Decision making is one of the most important parts of any aspect of life. It affects the present and both immediate and long-term future. Of course, it has a huge impact on every project, naturally including engineering projects. There is a vast number of techniques and methods to help one to come up with a final decision. In this article, the focus is the MCDA analysis in decision making. In decision making, there are different tools or criteria, such as Cost - Benefit Analysis (CBA) or the Multi Criteria Decision Analysis (MCDA). On one hand, CBA focus on the quantitative part of the project in order to reach a decision, specially focusing on monetary terms, currency change and various rates, such as inflation or consumer surplus. On the other hand, MCDA involves many other criteria, mostly qualitative, in order to reach a decision. Within MCDA, naturally, there are different techniques to use, the two main ones are AHP and Smart. As mentioned previously, the focus of this paper will be the MCDA methods in decision making. Initially, there will be an introduction on the history of the decision making and where the term comes from. Sequentially, there will be an explanation on both CBA and MCDA to reach a full understanding for both tools and comparing them. After this section, there will be a deeper explanation on the MCDA analysis, explaining the different types of MCDA and providing examples, pros and cons. Finally, there will be a conclusion on the involvement of MCDA analysis and methods in the decision making, focusing on engineering projects. |
__TOC__ | __TOC__ | ||
| Line 7: | Line 7: | ||
== History of Decision Making == | == History of Decision Making == | ||
| − | During the middle of the last century, Chester Bernard created the term "decision making". It was intended to | + | During the middle of the last century, Chester Bernard created the term "decision making" <ref name="origen"/>. It was intended to be a replacement and a narrower descriptor for "resource allocation and policy making". Additionally, it was an intended term for how managers though about what decisions to make at a certain time. Also, William Starbruck, professor in University of Oregon clearly stated that "Decision implies the end of deliberation and the beginning of action." <br /> <br /> |
Barnard along with others such as James March, Herbert Simon and Henry Mintberg laid the foundation for the study of managerial decision making. It tried to find answers to the questions of who makes decisions, and how. | Barnard along with others such as James March, Herbert Simon and Henry Mintberg laid the foundation for the study of managerial decision making. It tried to find answers to the questions of who makes decisions, and how. | ||
| − | The study of decision making involves a numerous | + | The study of decision making involves a numerous number of disciplines such as mathematics, sociology, psychology, economics, etc. It also investigated different risk and organizational behaviours in relation to achieving the best outcome. <br /> <br /> |
| − | A big participant of Decision Making is risk analysis, which has evolved vastly throughout the years. It was not until World War I that risk was | + | A big participant of Decision Making is risk analysis, which has evolved vastly throughout the years. It was not until World War I that risk was examined with economic analysis, thanks to Frank Knight in 1921. Knight distinguished between risk, when the probability of an outcome is possible to calculate and an uncertainty, when the probability of that outcome is unknowable. Nowadays, thanks to technology, Internet and Artificial Intelligence, tools have been created in order to improve the decision-making techniques and its outcomes. |
| − | == Types of Decision Making tools == | + | == Types of Decision-Making tools == |
| − | The main two analysis tools in the Decision Making | + | The main two analysis tools in the Decision-Making environment are Cost - Benefit Analysis and Multi - Criteria Decision Analysis. In this article, the focus will fall on MCDA. |
=== CBA === | === CBA === | ||
| − | Cost - Benefit Analysis (CBA) is a tool that is essential in order to support the decision making process. A CBA consists of quantitative data of a project, that being the enumeration and valuation in monetary terms of every cost and benefit of that project. The main result of a CBA is the Net Present Value, which in case of being positive, means that the benefits exceed costs over the project's lifetime. So, naturally, the goal is to reach a positive Net Present Value. <br /> | + | Cost - Benefit Analysis (CBA) is a tool that is essential in order to support the decision-making process. A CBA consists of quantitative data of a project, that being the enumeration and valuation in monetary terms of every cost and benefit of that project. The main result of a CBA is the Net Present Value, which in case of being positive, means that the benefits exceed costs over the project's lifetime. So, naturally, the goal is to reach a positive Net Present Value. <br /> |
This method is recommended when there are not any assets or effects of the decision making that do not involve money or are not assigned a monetary value. The CBA considers different values such as discount rate or consumer surplus, which helps to reach much more precise and realistic results, especially for projects who have a considerable life span or, specifically in engineering projects, have had a long construction period. <br /> <br /> | This method is recommended when there are not any assets or effects of the decision making that do not involve money or are not assigned a monetary value. The CBA considers different values such as discount rate or consumer surplus, which helps to reach much more precise and realistic results, especially for projects who have a considerable life span or, specifically in engineering projects, have had a long construction period. <br /> <br /> | ||
Furthermore, CBA can be complemented with the MCDA, making use of the qualitative data involving the project and improving the outcome of the decision and lastly, the project itself. | Furthermore, CBA can be complemented with the MCDA, making use of the qualitative data involving the project and improving the outcome of the decision and lastly, the project itself. | ||
| Line 24: | Line 24: | ||
On the other hand, the CBA method does not consider all the effects in most cases. The geopolitical and strategical issues have a vast influence in most of the projects and the CBA method does not include that. <br /> <br /> | On the other hand, the CBA method does not consider all the effects in most cases. The geopolitical and strategical issues have a vast influence in most of the projects and the CBA method does not include that. <br /> <br /> | ||
Furthermore, MCDA may be seen as an extension of the CBA. The CBA just represents a small part of the decision-making process, so MCDA makes it possible, in just one approach, to combine the CBA with the rest of qualitative effects. To achieve that, it is necessary to perform a previous decision process, which is subjective and assigns weights to each effect involved in the project, including the CBA. <br /> <br /> | Furthermore, MCDA may be seen as an extension of the CBA. The CBA just represents a small part of the decision-making process, so MCDA makes it possible, in just one approach, to combine the CBA with the rest of qualitative effects. To achieve that, it is necessary to perform a previous decision process, which is subjective and assigns weights to each effect involved in the project, including the CBA. <br /> <br /> | ||
| − | Finally, the previous process, can be performed in most cases since usually monetary and political or strategic effects are involved in most projects. Otherwise, in the table below, it is shown which methods ought to be used for each scenario. | + | Finally, the previous process, can be performed in most cases since usually monetary and political or strategic effects are involved in most projects. Otherwise, in the table below <ref name="libro"/>, it is shown which methods ought to be used for each scenario. |
| − | [[File: imagen.png]] | + | [[File: imagen.png|frame|none|alt=Alt text|Table 1: MCDA vs CBA]] |
== MCDA == | == MCDA == | ||
=== History === | === History === | ||
| − | The earliest MCDA references that are known go back to the eighteenth century referred to Benjamin Frankling where he stated "Take a sheet of paper. On one side write the arguments | + | The earliest MCDA references that are known go back to the eighteenth century referred to Benjamin Frankling where he stated "Take a sheet of paper. On one side write the arguments in favour of a decision: on the other side the arguments against. Cross out arguments on each side of the paper that are relative of equal importance. When all the arguments on one side have been crossed out, the side with arguments not crossed out is the side of the argument that should be supported” <ref> Barford, M., 2021. Screening analysis and outranking techniques. DTU </ref>. <br /> |
| − | There are other main names that had a considerable impact on the decision making as we know today. Some of those | + | There are other main names that had a considerable impact on the decision making as we know today. Some of those are Marquis de Condorcet, who wrote an essay on the application of analysis to the probability of majority decisions; George Cantor, who created set theory; or Francis Edgeworth, who integrated mathematical concepts to decision making. <br /> <br /> |
Nowadays, the present MCDA field involves investigation on different approaches which are descriptive, normative, prescriptive and constructive. The constructive approach is normally used by the French school which bases his process in outranking, while the normative approach is followed by the American school. <br /> <br /> | Nowadays, the present MCDA field involves investigation on different approaches which are descriptive, normative, prescriptive and constructive. The constructive approach is normally used by the French school which bases his process in outranking, while the normative approach is followed by the American school. <br /> <br /> | ||
Two big names on the most recent MCDA era are Bernard Roy and Thomas Saaty who both passed away in 2017. | Two big names on the most recent MCDA era are Bernard Roy and Thomas Saaty who both passed away in 2017. | ||
| Line 48: | Line 48: | ||
Firstly, the MCDA method does not give an absolute value that informs the decision taker to go forward with a project or not like the CBA does, where if it results in a positive Net Present Value, the project can go forward. It mainly only allows to compare between different projects. <br /> | Firstly, the MCDA method does not give an absolute value that informs the decision taker to go forward with a project or not like the CBA does, where if it results in a positive Net Present Value, the project can go forward. It mainly only allows to compare between different projects. <br /> | ||
Furthermore, due to the necessity of the pre-decision-making process, it makes MCDA time consuming and, in some cases, also resource consuming. <br /> | Furthermore, due to the necessity of the pre-decision-making process, it makes MCDA time consuming and, in some cases, also resource consuming. <br /> | ||
| − | To conclude, the election of weights in the MCDA method is crucial since it | + | To conclude, the election of weights in the MCDA method is crucial since it influences the whole outcome of the process. Due to that, the weight assignment is a really delicate process where any false step might null the whole assessment. |
| Line 59: | Line 59: | ||
There are various steps in the SMART technique process. These are: <br /> | There are various steps in the SMART technique process. These are: <br /> | ||
1. Identify the alternatives and the criteria <br /> | 1. Identify the alternatives and the criteria <br /> | ||
| − | 2. Assign each alternative score for each | + | 2. Assign each alternative score for each criterion <br /> |
| − | 3. Select a weight for each | + | 3. Select a weight for each criterion, typically between 0 and 100 <br /> |
4. Multiply the score for each criteria weight and obtain a total overall score for each alternative. <br /> | 4. Multiply the score for each criteria weight and obtain a total overall score for each alternative. <br /> | ||
5. Make a decision | 5. Make a decision | ||
===== SMARTER ===== | ===== SMARTER ===== | ||
| − | SMART Exploiting Ranks or SMARTER is a simplified version of SMART. It deals with some of the difficulties involving the weights of the criteria. This simplification was launched by Edwards and Barron. It uses simple criteria ranking, so the only process that needs to be done is to order the criteria from most important to less important. With this ranking, then, there are different kinds of rank distributions which will give in output that results in weights for each | + | SMART Exploiting Ranks or SMARTER is a simplified version of SMART. It deals with some of the difficulties involving the weights of the criteria. This simplification was launched by Edwards and Barron. It uses simple criteria ranking, so the only process that needs to be done is to order the criteria from most important to less important. With this ranking, then, there are different kinds of rank distributions which will give in output that results in weights for each criterion. The distributions are Rank order centroid (ROC), Rank sum (RS), Rank reciprocal (RR) and Rank order distribution (ROD). <br /> |
| − | They all have different calculations that end up associating a weight to each | + | They all have different calculations that end up associating a weight to each criterion. |
===== Pros and Cons of SMART technique ===== | ===== Pros and Cons of SMART technique ===== | ||
| − | The most | + | The most beneficial attribute of the SMART technique is, as the CBA, there is a quantitative outcome of the analysis, which is the total overall score. This situation eases the final decision making by a considerable amount since you can compare numerical scores instead of subjective and qualitative results. <br /> <br /> |
| − | On the other hand, the main | + | On the other hand, the main disadvantage of using the SMART technique is that, due to the subjective activities which are selecting the weights, criteria or ranking, it means that the results from the technique do not mean that the selected choice is always the right one. Also, some calculations for the different weight contributions for the SMARTER technique tend to be really complex and difficult sometimes. |
==== The Analytical Hierarchy Process (AHP) ==== | ==== The Analytical Hierarchy Process (AHP) ==== | ||
| − | The Analytical Hierarchy Process (AHP) was created in 1977 by Saaty. It is considered the formalization of our intuitive understanding of a complex problem using a hierarchical structure (Hwand and Yoon, 1995). The most | + | The Analytical Hierarchy Process (AHP) was created in 1977 by Saaty. It is considered the formalization of our intuitive understanding of a complex problem using a hierarchical structure (Hwand and Yoon, 1995). The most appropriate time to use this method is when there is a problem or a project that needs to satisfy multiple objectives. One of the up sides of this method is that while being a quite complex mathematical procedure, it can be easily implemented in basic software like Excel. <br /> <br /> |
| − | As mentioned before, the AHP is | + | As mentioned before, the AHP is borne on attributes hierarchy, which have at least three levels: the overall goal, the multiple criteria, and all the alternatives. In some situations, there are more than three levels since there can be sub - levels such as sub criteria. <br /> <br /> |
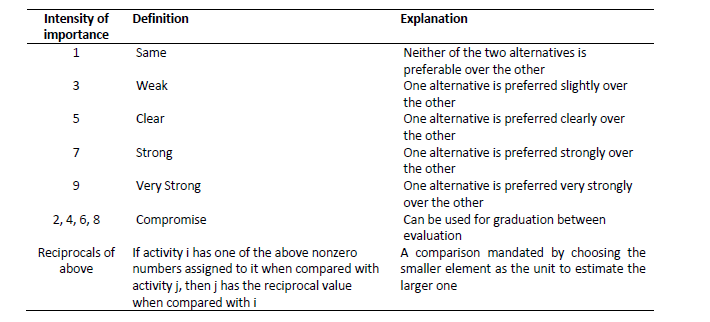
| − | One of the first | + | One of the first steps is, after assigning the different weights to each criterion, is to perform a pair-wise comparison between the different alternatives of the decision-making process. Saaty, in order to ease that process, created a nine-point intensity scale of importance between the two elements. The scale is shown in the following table <ref name="libro"/> |
| − | [[File:tabla.png]] | + | [[File: tabla.png|frame|none|alt=Alt text|Table 2: AHP scale]] |
| − | The next step is to combine all the pair-wise comparisons between the alternatives and merge it into a matrix for each | + | The next step is to combine all the pair-wise comparisons between the alternatives and merge it into a matrix for each criterion. A project with three alternatives and four criteria would have results <ref name="libro"/> such as: |
| − | [[File:tabla2.png]] | + | [[File: tabla2.png|frame|none|alt=Alt text|Table 3: Alternatives combination]] |
| − | After obtaining these | + | After obtaining these matrices, there are different methods and options to perform with these obtained matrices. <br /> <br /> |
| − | One of them is the eigen vector method, which only consists of obtaining the eigen values of the different matrixes. | + | One of them is the eigen vector method, which only consists of obtaining the eigen values of the different matrixes. Sequentially, the next step is to multiply each eigen value for each weight of the criteria, obtaining overall scores for the different alternatives. <br /> <br /> |
| − | Other method is the geometric mean method. It consists | + | Other method is the geometric mean method. It consists of the calculation of the geometric mean for each row of each matrix and obtaining like that, the overall scores for each alternative. <br /> |
| − | The AHP allows to check how inconsistent the | + | The AHP allows to check how inconsistent the assessment was. This can be possible with the eigen vector method. It provides a consistency ratio, which, the higher it is, the more consistent the matrix is. It derives from the maximum eigen value and is calculated as<ref name="libro"/>: <br /> |
| − | [[File:cr.png]] | + | [[File: cr.png|frame|none|alt=Alt text|Image 1: Consistency Ratio Calculation ]] |
| − | ===== | + | ===== Strengths of AHP ===== |
- '''''Formal structuring of the problem''''': It provides a formal structure to problems. <br /> | - '''''Formal structuring of the problem''''': It provides a formal structure to problems. <br /> | ||
| − | - '''''Simplicity of Pair-wise comparisons'''' | + | - '''''Simplicity of Pair-wise comparisons''''‘: It allows the decision maker to focus on the smallest details of the decision-making process. <br /> |
- '''''Consistency ratio''''': It has the possibility to be checked on its consistency aspect. <br /> | - '''''Consistency ratio''''': It has the possibility to be checked on its consistency aspect. <br /> | ||
- '''''Versatility''''': It can be applied to a wide range of types of problems. <br /> | - '''''Versatility''''': It can be applied to a wide range of types of problems. <br /> | ||
| Line 103: | Line 103: | ||
===== Weaknesses of AHP ===== | ===== Weaknesses of AHP ===== | ||
- '''''Verbal to numeric conversion''''': It requires to convert all the judgements made by the decision makers to a numeric scale from 1 to 9. <br /> | - '''''Verbal to numeric conversion''''': It requires to convert all the judgements made by the decision makers to a numeric scale from 1 to 9. <br /> | ||
| − | - '''''Lack of flexibility''''': If a new alternative is introduced during the process, it | + | - '''''Lack of flexibility''''': If a new alternative is introduced during the process, it changes the whole ranking and, therefore, the weights, which are the base of this process. <br /> |
| − | - '''''1 to 9 scale''''': It derivates to some inconsistencies due that, if you consider alternative 1 seven times better in one | + | - '''''1 to 9 scale''''': It derivates to some inconsistencies due that, if you consider alternative 1 seven times better in one criterion than alternative 2, that cannot be possible to show in that scale. <br /> |
| − | - '''''Size limited''''': If there is a big | + | - '''''Size limited''''': If there is a big number of alternatives and criteria there can be a vast number of pair-wise comparisons. For example, if there are 8 alternatives along with 8 criteria, it can lead to 224 pair-wise comparisons. <br /> |
===== The multiplicative AHP (REMBRANDT) ===== | ===== The multiplicative AHP (REMBRANDT) ===== | ||
| − | In order to solve some of the weaknesses that the standard AHP presents, the multiplicative AHP, which also goes by the name of REMBRANDT (Ratio Estimation in Magnitudes or | + | In order to solve some of the weaknesses that the standard AHP presents, the multiplicative AHP <ref> Olson, D., Fliedner, G. and Currie, K., 1993. Comparison of the REMBRANDT system with analytic hierarchy process. European Journal of Operations Research, 82. </ref>, which also goes by the name of REMBRANDT (Ratio Estimation in Magnitudes or Deci-Bells to Rate Alternatives which are non-DominaTed), was created in 1992 by Lootsma. <br /> <br /> |
| − | It aims to fix three specific weaknesses of the standard AHP process. First, the 1 to 9 scale of AHP. Lootsma proposed this new scale, which is on a geometric scale. <br /> | + | It aims to fix three specific weaknesses of the standard AHP process. First, the 1 to 9 scale of AHP. Lootsma proposed this new scale<ref name="libro"/>, which is on a geometric scale. <br /> |
| − | [[File:rembrandt.png| | + | [[File:rembrandt.png|frame|none|alt=Alt text|Table 4: AHP vs REMBRANDT Scale ]] |
| − | The second weakness aimed to be fixed is the calculation of scores. As mentioned previously, in the standard AHP, if you introduce a new alternative in mid-process it breaks it. So REMBRANDT uses a logarithmic regression which avoids this error to | + | The second weakness aimed to be fixed is the calculation of scores. As mentioned previously, in the standard AHP, if you introduce a new alternative in mid-process, it breaks it. So, REMBRANDT uses a logarithmic regression which avoids this error to occur. <br /> <br /> |
| − | The third and last point intends to fix how the individual scores are aggregated. The AHP uses a method based on calculating the eigen vectors and adding the multiplication of scores by the criteria weight. REMBRANDT uses geometric mean calculation to reach the scores. <br /> | + | The third and last point intends to fix how the individual scores are aggregated. The AHP uses a method based on calculating the eigen vectors and adding the multiplication of scores by the criteria weight. REMBRANDT uses geometric mean calculation to reach the scores. <br /> <br /> |
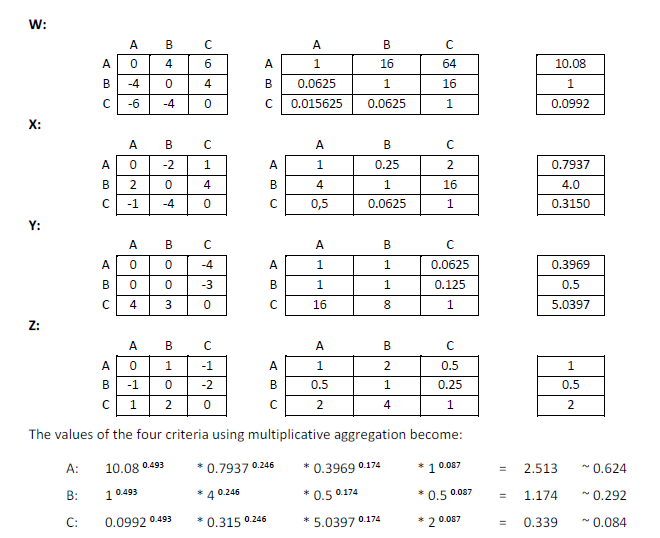
| − | In order to show in a better way how the process takes place, here is an example where there are three alternatives, A, B and C and four criteria W, X, Y and Z with weights 0.493 , 0.246, 0.174 and 0.087 respectively. | + | In order to show in a better way how the process takes place, here is an example<ref name="libro"/> where there are three alternatives, A, B and C and four criteria W, X, Y and Z with weights 0.493, 0.246, 0.174 and 0.087 respectively. |
| − | [[File:examplerembr.png]] | + | [[File: examplerembr.png|frame|none|alt=Alt text|Image 2: REMBRANDT Example ]] |
= Conclusion = | = Conclusion = | ||
| Line 126: | Line 126: | ||
Decision making plays a huge role in every company where it needs to be decided which path or projects need to be done to reach the company's goal. <br /> <br /> | Decision making plays a huge role in every company where it needs to be decided which path or projects need to be done to reach the company's goal. <br /> <br /> | ||
| − | Along with the main key requirements that need to be achieved during the election of which projects are going to be done which are , for example, budget, customer satisfaction, or internal return value, this paper intends to involucrate in higher scale the MCDA in the process of the decision making. <br /> | + | Along with the main key requirements that need to be achieved during the election of which projects are going to be done which are, for example, budget, customer satisfaction, or internal return value, this paper intends to involucrate in higher scale the MCDA in the process of the decision making. <br /> |
| − | MCDA can be an exceptional way to involucrate all the main criteria mentioned before in one unique process. It can involucrate both quantitative criteria, | + | MCDA can be an exceptional way to involucrate all the main criteria mentioned before in one unique process. It can involucrate both quantitative criteria, such as budget or internal rate of return; or qualitative criteria, like customer satisfaction. <br /> <br /> |
| − | This is why MCDA should be used more frequently due that involves as many aspects as the decision makers want to involver and lets them assess every alternative via | + | This is why MCDA should be used more frequently due that involves as many aspects as the decision makers want to involver and lets them assess every alternative via a unique process. |
= References = | = References = | ||
| + | <references> | ||
| + | <ref name= "origen"> Buchanan, L. and O’Connell, A., 2006. A brief History of Decision Making. Harvard Business Review, [online] </ref> | ||
| + | <ref name= "libro"> Barford, M. and Leleur, S., 2021. Decision Support and Strategic Assessment. 2nd ed. Technical University of Denmark: DTU Management Compendium. </ref> | ||
Latest revision as of 15:31, 18 March 2022
[edit] Abstract
Decision making is one of the most important parts of any aspect of life. It affects the present and both immediate and long-term future. Of course, it has a huge impact on every project, naturally including engineering projects. There is a vast number of techniques and methods to help one to come up with a final decision. In this article, the focus is the MCDA analysis in decision making. In decision making, there are different tools or criteria, such as Cost - Benefit Analysis (CBA) or the Multi Criteria Decision Analysis (MCDA). On one hand, CBA focus on the quantitative part of the project in order to reach a decision, specially focusing on monetary terms, currency change and various rates, such as inflation or consumer surplus. On the other hand, MCDA involves many other criteria, mostly qualitative, in order to reach a decision. Within MCDA, naturally, there are different techniques to use, the two main ones are AHP and Smart. As mentioned previously, the focus of this paper will be the MCDA methods in decision making. Initially, there will be an introduction on the history of the decision making and where the term comes from. Sequentially, there will be an explanation on both CBA and MCDA to reach a full understanding for both tools and comparing them. After this section, there will be a deeper explanation on the MCDA analysis, explaining the different types of MCDA and providing examples, pros and cons. Finally, there will be a conclusion on the involvement of MCDA analysis and methods in the decision making, focusing on engineering projects.
Contents |
[edit] Introduction
[edit] History of Decision Making
During the middle of the last century, Chester Bernard created the term "decision making" [1]. It was intended to be a replacement and a narrower descriptor for "resource allocation and policy making". Additionally, it was an intended term for how managers though about what decisions to make at a certain time. Also, William Starbruck, professor in University of Oregon clearly stated that "Decision implies the end of deliberation and the beginning of action."
Barnard along with others such as James March, Herbert Simon and Henry Mintberg laid the foundation for the study of managerial decision making. It tried to find answers to the questions of who makes decisions, and how.
The study of decision making involves a numerous number of disciplines such as mathematics, sociology, psychology, economics, etc. It also investigated different risk and organizational behaviours in relation to achieving the best outcome.
A big participant of Decision Making is risk analysis, which has evolved vastly throughout the years. It was not until World War I that risk was examined with economic analysis, thanks to Frank Knight in 1921. Knight distinguished between risk, when the probability of an outcome is possible to calculate and an uncertainty, when the probability of that outcome is unknowable. Nowadays, thanks to technology, Internet and Artificial Intelligence, tools have been created in order to improve the decision-making techniques and its outcomes.
[edit] Types of Decision-Making tools
The main two analysis tools in the Decision-Making environment are Cost - Benefit Analysis and Multi - Criteria Decision Analysis. In this article, the focus will fall on MCDA.
[edit] CBA
Cost - Benefit Analysis (CBA) is a tool that is essential in order to support the decision-making process. A CBA consists of quantitative data of a project, that being the enumeration and valuation in monetary terms of every cost and benefit of that project. The main result of a CBA is the Net Present Value, which in case of being positive, means that the benefits exceed costs over the project's lifetime. So, naturally, the goal is to reach a positive Net Present Value.
This method is recommended when there are not any assets or effects of the decision making that do not involve money or are not assigned a monetary value. The CBA considers different values such as discount rate or consumer surplus, which helps to reach much more precise and realistic results, especially for projects who have a considerable life span or, specifically in engineering projects, have had a long construction period.
Furthermore, CBA can be complemented with the MCDA, making use of the qualitative data involving the project and improving the outcome of the decision and lastly, the project itself.
[edit] MCDA vs CBA
While CBA reflects all the effects that can be monetarized and has the only goal of maximizing the Net Present Value, the MCDA method involves other effects that cannot be monetarized and are qualitative data.
There are clear benefits of the CBA method, which are that the conclusions of this analysis are clear and easy to compare to other projects since are given as a monetary unit value. Also, the rates that are used to perform this analysis are consistent between investments and over time. This allows to compare projects that have different timelines which is convenient for many cases.
On the other hand, the CBA method does not consider all the effects in most cases. The geopolitical and strategical issues have a vast influence in most of the projects and the CBA method does not include that.
Furthermore, MCDA may be seen as an extension of the CBA. The CBA just represents a small part of the decision-making process, so MCDA makes it possible, in just one approach, to combine the CBA with the rest of qualitative effects. To achieve that, it is necessary to perform a previous decision process, which is subjective and assigns weights to each effect involved in the project, including the CBA.
Finally, the previous process, can be performed in most cases since usually monetary and political or strategic effects are involved in most projects. Otherwise, in the table below [2], it is shown which methods ought to be used for each scenario.
[edit] MCDA
[edit] History
The earliest MCDA references that are known go back to the eighteenth century referred to Benjamin Frankling where he stated "Take a sheet of paper. On one side write the arguments in favour of a decision: on the other side the arguments against. Cross out arguments on each side of the paper that are relative of equal importance. When all the arguments on one side have been crossed out, the side with arguments not crossed out is the side of the argument that should be supported” [3].
There are other main names that had a considerable impact on the decision making as we know today. Some of those are Marquis de Condorcet, who wrote an essay on the application of analysis to the probability of majority decisions; George Cantor, who created set theory; or Francis Edgeworth, who integrated mathematical concepts to decision making.
Nowadays, the present MCDA field involves investigation on different approaches which are descriptive, normative, prescriptive and constructive. The constructive approach is normally used by the French school which bases his process in outranking, while the normative approach is followed by the American school.
Two big names on the most recent MCDA era are Bernard Roy and Thomas Saaty who both passed away in 2017.
[edit] Pros and Cons
[edit] Pros
While CBA reflects all the effects that can be monetarized and has the only goal of maximizing the Net Present Value, the MCDA method involves other effects that cannot be monetarized and are qualitative data.
There are clear benefits of the CBA method, which are that the conclusions of this analysis are clear and easy to compare to other projects since are given as a monetary unit value. Also, the rates that are used to perform this analysis are consistent between investments and over time. This allows to compare projects that have different timelines which is convenient for many cases.
On the other hand, the CBA method does not consider all the effects in most cases. The geopolitical and strategical issues have a vast influence in most of the projects and the CBA method does not include that.
Furthermore, MCDA may be seen as an extension of the CBA. The CBA just represents a small part of the decision-making process, so MCDA makes it possible, in just one approach, to combine the CBA with the rest of qualitative effects. To achieve that, it is necessary to perform a previous decision process, which is subjective and assigns weights to each effect involved in the project, including the CBA.
Finally, the previous process, can be performed in most cases since usually monetary and political or strategic effects are involved in most projects. Otherwise, in the table below, it is shown which methods ought to be used for each scenario.
[edit] Cons
Firstly, the MCDA method does not give an absolute value that informs the decision taker to go forward with a project or not like the CBA does, where if it results in a positive Net Present Value, the project can go forward. It mainly only allows to compare between different projects.
Furthermore, due to the necessity of the pre-decision-making process, it makes MCDA time consuming and, in some cases, also resource consuming.
To conclude, the election of weights in the MCDA method is crucial since it influences the whole outcome of the process. Due to that, the weight assignment is a really delicate process where any false step might null the whole assessment.
[edit] Main techniques
The two main techniques in the MCDA method are the Simple Multi – Attribute Rating Technique (SMART) and The Analytic Hierarchy Process (AHP).
[edit] The Simple Multi - Attribute Rating Technique (SMART)
The Simple Multi - Attribute Rating Technique, SMART technique is based on a linear additive model. Each alternative, which can be different projects obtain an overall score. This overall score are the sums of each individual criteria score multiplied by the criterion weight that has been assigned previously by the decision makers.
There are various steps in the SMART technique process. These are:
1. Identify the alternatives and the criteria
2. Assign each alternative score for each criterion
3. Select a weight for each criterion, typically between 0 and 100
4. Multiply the score for each criteria weight and obtain a total overall score for each alternative.
5. Make a decision
[edit] SMARTER
SMART Exploiting Ranks or SMARTER is a simplified version of SMART. It deals with some of the difficulties involving the weights of the criteria. This simplification was launched by Edwards and Barron. It uses simple criteria ranking, so the only process that needs to be done is to order the criteria from most important to less important. With this ranking, then, there are different kinds of rank distributions which will give in output that results in weights for each criterion. The distributions are Rank order centroid (ROC), Rank sum (RS), Rank reciprocal (RR) and Rank order distribution (ROD).
They all have different calculations that end up associating a weight to each criterion.
[edit] Pros and Cons of SMART technique
The most beneficial attribute of the SMART technique is, as the CBA, there is a quantitative outcome of the analysis, which is the total overall score. This situation eases the final decision making by a considerable amount since you can compare numerical scores instead of subjective and qualitative results.
On the other hand, the main disadvantage of using the SMART technique is that, due to the subjective activities which are selecting the weights, criteria or ranking, it means that the results from the technique do not mean that the selected choice is always the right one. Also, some calculations for the different weight contributions for the SMARTER technique tend to be really complex and difficult sometimes.
[edit] The Analytical Hierarchy Process (AHP)
The Analytical Hierarchy Process (AHP) was created in 1977 by Saaty. It is considered the formalization of our intuitive understanding of a complex problem using a hierarchical structure (Hwand and Yoon, 1995). The most appropriate time to use this method is when there is a problem or a project that needs to satisfy multiple objectives. One of the up sides of this method is that while being a quite complex mathematical procedure, it can be easily implemented in basic software like Excel.
As mentioned before, the AHP is borne on attributes hierarchy, which have at least three levels: the overall goal, the multiple criteria, and all the alternatives. In some situations, there are more than three levels since there can be sub - levels such as sub criteria.
One of the first steps is, after assigning the different weights to each criterion, is to perform a pair-wise comparison between the different alternatives of the decision-making process. Saaty, in order to ease that process, created a nine-point intensity scale of importance between the two elements. The scale is shown in the following table [2]
The next step is to combine all the pair-wise comparisons between the alternatives and merge it into a matrix for each criterion. A project with three alternatives and four criteria would have results [2] such as:
After obtaining these matrices, there are different methods and options to perform with these obtained matrices.
One of them is the eigen vector method, which only consists of obtaining the eigen values of the different matrixes. Sequentially, the next step is to multiply each eigen value for each weight of the criteria, obtaining overall scores for the different alternatives.
Other method is the geometric mean method. It consists of the calculation of the geometric mean for each row of each matrix and obtaining like that, the overall scores for each alternative.
The AHP allows to check how inconsistent the assessment was. This can be possible with the eigen vector method. It provides a consistency ratio, which, the higher it is, the more consistent the matrix is. It derives from the maximum eigen value and is calculated as[2]:
[edit] Strengths of AHP
- Formal structuring of the problem: It provides a formal structure to problems.
- Simplicity of Pair-wise comparisons'‘: It allows the decision maker to focus on the smallest details of the decision-making process.
- Consistency ratio: It has the possibility to be checked on its consistency aspect.
- Versatility: It can be applied to a wide range of types of problems.
[edit] Weaknesses of AHP
- Verbal to numeric conversion: It requires to convert all the judgements made by the decision makers to a numeric scale from 1 to 9.
- Lack of flexibility: If a new alternative is introduced during the process, it changes the whole ranking and, therefore, the weights, which are the base of this process.
- 1 to 9 scale: It derivates to some inconsistencies due that, if you consider alternative 1 seven times better in one criterion than alternative 2, that cannot be possible to show in that scale.
- Size limited: If there is a big number of alternatives and criteria there can be a vast number of pair-wise comparisons. For example, if there are 8 alternatives along with 8 criteria, it can lead to 224 pair-wise comparisons.
[edit] The multiplicative AHP (REMBRANDT)
In order to solve some of the weaknesses that the standard AHP presents, the multiplicative AHP [4], which also goes by the name of REMBRANDT (Ratio Estimation in Magnitudes or Deci-Bells to Rate Alternatives which are non-DominaTed), was created in 1992 by Lootsma.
It aims to fix three specific weaknesses of the standard AHP process. First, the 1 to 9 scale of AHP. Lootsma proposed this new scale[2], which is on a geometric scale.
The second weakness aimed to be fixed is the calculation of scores. As mentioned previously, in the standard AHP, if you introduce a new alternative in mid-process, it breaks it. So, REMBRANDT uses a logarithmic regression which avoids this error to occur.
The third and last point intends to fix how the individual scores are aggregated. The AHP uses a method based on calculating the eigen vectors and adding the multiplication of scores by the criteria weight. REMBRANDT uses geometric mean calculation to reach the scores.
In order to show in a better way how the process takes place, here is an example[2] where there are three alternatives, A, B and C and four criteria W, X, Y and Z with weights 0.493, 0.246, 0.174 and 0.087 respectively.
[edit] Conclusion
After reading this article, it appears clear that MCDA offers a huge range of opportunities for the decision makers in order to assess the projects from where they have to decide.
Decision making plays a huge role in every company where it needs to be decided which path or projects need to be done to reach the company's goal.
Along with the main key requirements that need to be achieved during the election of which projects are going to be done which are, for example, budget, customer satisfaction, or internal return value, this paper intends to involucrate in higher scale the MCDA in the process of the decision making.
MCDA can be an exceptional way to involucrate all the main criteria mentioned before in one unique process. It can involucrate both quantitative criteria, such as budget or internal rate of return; or qualitative criteria, like customer satisfaction.
This is why MCDA should be used more frequently due that involves as many aspects as the decision makers want to involver and lets them assess every alternative via a unique process.
[edit] References
- ↑ Buchanan, L. and O’Connell, A., 2006. A brief History of Decision Making. Harvard Business Review, [online]
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Barford, M. and Leleur, S., 2021. Decision Support and Strategic Assessment. 2nd ed. Technical University of Denmark: DTU Management Compendium.
- ↑ Barford, M., 2021. Screening analysis and outranking techniques. DTU
- ↑ Olson, D., Fliedner, G. and Currie, K., 1993. Comparison of the REMBRANDT system with analytic hierarchy process. European Journal of Operations Research, 82.