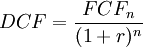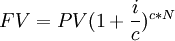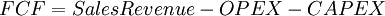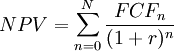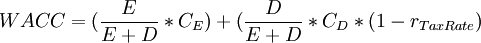Discounted cash flow
(→Time value of money) |
(→Investopedia.com, Discounted Cash Flow (DCF) Explained With Formula and Examples) |
||
| (159 intermediate revisions by one user not shown) | |||
| Line 2: | Line 2: | ||
| − | This page | + | This page refers to the discounted cash flow (DCF) method regarding projects and investments <ref name="PMI" />, which is used to evaluate if a project is worth pursuing based on its future financial merits. |
| − | Discounted Cash Flow | + | Discounted Cash Flow often used to calculate and estimate the value of any investment or a project by projecting its future cash flows and then discounting them back to their present value (PV), meaning in todays money. <ref name="DCF" /> |
| − | The | + | The rationale behind the use discounted cash flow is that an investment in a project's value is equal to the sum of its forecasted future cash flows, discounted at an appropriate (often with lots of assumptions) rate. It is discounted due to the principle of the time value of money and the potential risk involved in the investment <ref name="DCF" />. The time value of money refers to the tendency for money to lose its value over time. This sum of the all the discounted cash flows in a forecasted period is known as the Net Present Value (NPV).<ref name="DCF" /> Since the discounted cash flow is such a big part of the NPV, the two are almost interchangable when it comes to calculations. |
| − | + | == Origin == | |
| − | |||
| − | = | + | The idea of discounted cash flow has been utilized in one way or another for many years, and can even be traced back to the coal industry in the 1700 hundreds <ref name="Origin" />. However, The modern version trace back to the early 20th century, where it was used in finance and to analyse investments. |
| + | One of the most influencial and modern uses of DCF was in 1930 by American economist Irving Fisher in "The Theory of Interest." Fisher used DCF to calculate the sum present value of future cash flows, which he coined the "net present value" of an investment.<ref name="RHPARKER" /> Since then, this method has been widely used in valuation, including in finance, investment, and project management. | ||
| − | + | == Math section == | |
| − | + | ||
| − | + | ||
| − | + | === Formula === | |
| − | + | The discounted cash flow is a way of calculating the present value of a future free cash flow, evaluated at a given discount rate. That means any single given cash flow can be brought back to the value of the present. The formula for the DCF can be seen below. | |
| − | + | <math> DCF = \frac{FCF_n}{(1+r)^n} </math> <ref name="DCF" /> | |
| − | + | Where | |
| − | + | ||
| − | + | <math> FCF </math> is a free cash flow. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math> n </math> is the year in the forecasted period <math> N </math>. | |
| − | == | + | <math> r </math> is the discount rate. |
| − | A | + | |
| + | As the present value of a single cash flow is not that useful on its own, usually the formula is applied on a number of cash flows, corresponding to each year in a period. When done like this, the formula becomes a series of discounted cash flows added together. An example of this can be seen below. | ||
| + | |||
| + | <math> DCF = \frac{FCF_1}{(1+r)^1} +\frac{FCF_2}{(1+r)^2} +...\frac{FCF_N}{(1+r)^N} </math> | ||
| + | |||
| + | This can be used to assign value to a project or a business by assessing the cash flows it will generate within the forecasted period <math> N </math>. Since the formula operates with increasing years, the further away in the future the cash flow is, the lower the present value of it will be. This is due to the time value of money. | ||
| + | |||
| + | === Discount Rate === | ||
| + | |||
| + | The discounted cash flow formula is highly dependent on the discount rate <math> r </math>. The discount rate is a rate of interest which is applied to the future cash flows of an investment or a business, which determines the final Net Present Value (NPV). <ref name="DiscountRate" /> There are several ways of determining the appropriate discount rate, but some level of uncertainty will always occur. For many intents and purposes, the discount rate is assumed to a certain value. However, for more precise values, there are ways of estimating it. Some of the most prevalent types of discount rate include<ref name= "DiscountRate" /> : | ||
| + | |||
| + | *Weighted Average Cost of Capital (WACC) | ||
| + | *Hurdle Rate | ||
| + | *Cost of Equity | ||
| + | *Cost of Debt | ||
| + | |||
| + | In this article, the WACC will be discussed in a later section. | ||
| + | |||
| + | === Example === | ||
| + | |||
| + | A simple example is given below. In this case, the DCF is only calculated for a single cash flow, 1 year from present. In this way, the result will be value of a cash flow a year from now in today's money. | ||
| + | In this simple example, the business is a lemonade stand. The lemonade stand has a yearly total cost of 100$ and a yearly total revenue of 200$ in year 1. This will mean that the free cash flow (FCF) for year 1 is: | ||
| + | |||
| + | <math> FCF_1 = 200$ - 100$ = 100$ </math> | ||
| + | |||
| + | Now, it is assumed that there is a discount rate <math> r </math> of 6%. With this, the final DCF for year <math> n=1 </math> can be calculated as: | ||
| + | |||
| + | <math> DCF_1 = \frac{FCF_1}{(1+r)^n} = \frac{100$}{(1+0.06)^1} = 88.99$ </math> | ||
| − | + | This means that even though the lemonade stand will generate 100$ next year, this is only worth 88.99$ today. | |
| − | + | ||
| − | + | ||
== Application == | == Application == | ||
| − | + | This section highlights the application of DCF as well as important principles that are deeply connected to the method of discounting cash flows. | |
=== Time value of money === | === Time value of money === | ||
| − | |||
| − | |||
| − | + | The time value of money (TVM) is an important concept that states that the value of money changes over time. Practically, this means that any sum of money today is worth more than the exact same amount of money in the future, and herefrom comes the well known expression "A dollar today is worth more than a dollar tomorrow." The reason behind this phenomenon is that money today has the potential and ability to be used to generate more money by investing them in clever ways, whereas money in the future can only be invested in the future, and thus loses its earnings potential (that is, for the present). Furthermore, factors like inflation and interest rates contribute to the fact that money can lose its value over time.<ref name="TVM" /> | |
| + | The time value of money is an then an extremely important principle in projects and especially when investing in them initially, as it helps project managers and coorporations make informed decisions about how to invest their resources smartly and which project to pursue. The TVM can be calculated both for present values and future values. The equation for future value (FV) can be seen below: | ||
| − | + | <math> FV = PV(1+\frac{i}{c})^{c*N} </math> <ref name="TVM" /> | |
| − | + | ||
| − | + | ||
| − | + | Where | |
| + | |||
| + | <math> FV </math> is the future value | ||
| + | |||
| + | <math> PV </math> is the present value | ||
| + | |||
| + | <math> i </math> is the interest rate | ||
| + | |||
| + | <math> c </math> is the compoundings per year | ||
| + | |||
| + | <math> N </math> is the number of years | ||
| + | |||
| + | This equation can be used to estimate the value of a sum of money today in the future. It is highly dependent on the number of compounding periods per year. <ref name="Compounding" /> | ||
| + | |||
| + | === Free Cash Flow === | ||
| + | The free cash flow (FCF) is the cash flow that is available after a business pays for the costs of continued operations, like operating expences and capital expenditures. Generally, the more free cash flow a business or a project has, the more attractive it will be for investors, as it will be able to invest in new opportunities. There are multiple ways of calculating the free cash flows depending on the level of precision and complexity desired. A simple model for calculating this can be seen below. | ||
| + | |||
| + | <math>F C F = Sales Revenue - OPEX - CAPEX </math> <ref name="FCF" /> | ||
| + | |||
| + | The sales revenue is the money going into the project or the business, hence the positive sign. | ||
| + | |||
| + | OPEX is the Operational Expenditure and it refers to the recurring short-term cost of maintaining the operations and keeping a project or a company running on a daily basis. This could be the cost of necessities such as rent, electricity, staff salaries, and other costs associated with delivering a project's desired outcome on a day-to-day scale. <ref name="OPEX"/> | ||
| + | |||
| + | CAPEX is the Capital Expenditures, which refers to the amnount fo money a company or a project need to invest in acquiring its long-term assets needed to start operations. This can include assets such as property, equipment, or technology. <ref name = "CAPEX" /> Capital Expenditures are generally more expensive and long-term than other expenses, such as the operational expenditure, and are considered investments in the company's future. | ||
| + | |||
| + | The Free Cash Flow is in this instance calculated for a single year. However, doing it for multiple years is necessary. Generally speaking, the FCF needs to be projected until it reaches a steady state (typically 5 to 10 years).<ref name="DCF2" /> | ||
| + | |||
| + | ==== Example ==== | ||
| + | |||
| + | As the previous example mentioned, the free cash flow needed to be used in the DCF formula. However, the equation for finding the FCF for a lemonade stand was somewhat simplified. | ||
| + | As can be seen from the equation for FCF, the free cash flow equals the total sales revenue (or other generated income) minus the total costs. However, this time the costs are divided into two categories. Operational costs and capital costs. | ||
| + | Using the same numbers as the previous example, we have that the total sales revenue of the lemonade stand is 200$. The operational expenses are costs such as ingredients to make the lemonade (sugar, lemons, ice etc.). These are the things that are needed on a daily basis. On the other hand the capital expenses might be things like the actual stand and the sign - things that are invested in once in the beginning of the "venture." | ||
| + | |||
| + | We than have that: | ||
| + | |||
| + | <math> SalesRevenue = 200$ </math> | ||
| + | |||
| + | <math> OPEX = 60$ </math> | ||
| + | |||
| + | <math> CAPEX = 40$ </math> | ||
| + | |||
| + | Putting it all into the formula, we get the same free cash flow for the first year as in the DCF example: | ||
| + | |||
| + | <math> FCF = SalesRevenue - OPEX - CAPEX = 200$ - 60$ - 40$ = 100$ </math> | ||
| + | |||
| + | As this is just the free cash flow for one year, when calculating the NPV, cash flows for multiple years are required. | ||
=== Net Present Value (NPV)=== | === Net Present Value (NPV)=== | ||
| − | |||
| − | + | The Net Present Value (NPV) is another financial method that is used to evaluate the merits of project based on the discounted cash flow, and whether it is worth investing in. <ref name = "NPV" /> It is often used to address the financial attractiveness of long-term investments, this could include a project like construction of new plant for a big production company. The value of the NPV would then tell something about the monetary value of the investent, and if it would generate a net loss or a net positive if made. NPV is extremely closely related to the discounted cash flow (DCF) as mentioned previously in the article, as it is merely the sum of all the discounted cash flows in a given forecasted period of time. This means that the formula and the method of calculation is almost identical to that of DCF. The formula for NPV can be seen below: | |
| − | |||
| − | + | <math> NPV = \sum_{n=0}^N \frac{FCF_n}{(1+r)^n} </math> <ref name = "NPV" /> | |
| − | + | It is clear to see that this is identical to the DCF-formula, the only difference being the summation over all years in the time period <math> N </math>. This formula can then be used to decide whether a project is worth investing in. | |
| + | |||
| + | ==== Net Present Value Rule ==== | ||
| + | |||
| + | The net present value rule is a simple rule that can identify whether or not an investment should be made by companies and project managers, based on the estimated value of the NPV. The rule can be seen on the table below<ref name = "NPV" /> . | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! NPV = 0 | ||
| + | ! The investment will bring net zero value in present money terms. | ||
| + | |- | ||
| + | | NPV < 0 | ||
| + | | The investment will result in a net loss. Investment should not be made. | ||
| + | |- | ||
| + | | NPV > 0 | ||
| + | | The investment will result in a net gain. Investment should be made. | ||
| + | |} | ||
| + | |||
| + | |||
| + | This rule indicates that an investment should only be made (in monetary terms) if the net present value is positive. | ||
| + | |||
| + | |||
| + | ==== Example ==== | ||
| + | |||
| + | Now we make a new example of the lemonade stand, to see if it is worthwhile to invest in the lemonade stand. We assume that this will be over a 5 year period, meaning <math> N = 5 </math>. On the following table the cash flow for each year can be seen (here we assume that the free cash flow has already been calculated, with sales and costs). | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Discount Rate | ||
| + | ! 6% | ||
| + | |- | ||
| + | | Initial Investment | ||
| + | | 200$ | ||
| + | |- | ||
| + | | Year 1 | ||
| + | | 60$ | ||
| + | |- | ||
| + | | Year 2 | ||
| + | | 70$<br /> | ||
| + | |- | ||
| + | | Year 3 | ||
| + | | 40$ | ||
| + | |- | ||
| + | | Year 4 | ||
| + | | 50$ | ||
| + | |- | ||
| + | | Year 5 | ||
| + | | 60$ | ||
| + | |} | ||
| + | |||
| + | Note that the initial investment is considered now. This is the cost that is incurred in the present, i.e. the investment made in the business in year 0. Now we want to use the formula for NPV to see if the initial investment is worth it in the long run - that is the next 5 years. | ||
| + | |||
| + | <math> NPV = \frac{-200}{(1+0.06)^0} + \frac{60}{(1+0.06)^1} +\frac{70}{(1+0.06)^2} +\frac{40}{(1+0.06)^3} +\frac{50}{(1+0.06)^4} +\frac{60}{(1+0.06)^5} = 36.92$ </math> | ||
| + | |||
| + | In this case, since we have a positive net present value of <math> 36.92$ </math>, it means that the lemonade stand is worth investing in. This essentially means that the stand makes this amount of money over the next 5 years, accounting for all costs. | ||
=== Working Average Cost of Capital (WACC) === | === Working Average Cost of Capital (WACC) === | ||
| − | The Weighted Average Cost of Capital (WACC) is a | + | The Weighted Average Cost of Capital (WACC) is a way of measuring the cost of financing for a company. This financing can come in two types: dept and equity. Both of these have an associated cost, that is relevant when calculating the WACC. As mentioned earlier, the WACC is often used as the discount rate in the formulas for DCF and NPV.<ref name="WACC" /> The formula for WACC can be seen below. |
| − | + | <math> WACC = ( \frac{E}{E+D} * C_E) + ( \frac{D}{E+D} * C_D * (1-r_{TaxRate}) </math> <ref name="WACC" /> | |
| − | + | Where | |
| − | + | <math> E </math> is the market value of the firm's equity | |
| − | + | <math> D </math> is the market value of the firm's dept | |
| − | + | <math> C_E </math> is the cost of equity | |
| − | + | ||
| − | + | <math> C_D </math> is the cost of dept | |
| − | + | ||
| − | + | ||
| − | + | <math> r_{TaxRate} </math> is the tax rate | |
| − | + | ||
| − | + | This formula can then be used to get a more precise estimation of the discount rate, and subsequently be used to calculate the discounted cash flow and the net present value.<ref name="WACC" /> | |
| − | + | ||
| − | + | === Terminal Value === | |
| − | + | ||
| − | + | The Terminal Value (TV) is the value of the firm or the project after the forecasted period. It is another important method that is used when trying to calculate the present value of a firm or an investment. As the discounted cash flow is done over a certain forecasted period, ususally a couple of years, the NPV of the company will be based only on the present values of the cash flows within this time period. However, in reality, companies keep going after the end of the forecasted period. This means that a company or the product of a completed project will still continue to generate cash flows after the forecasted period. The Terminal Value is then a technique used to capture all the cash flows that comes after the forecasted period and to infinity. This is done by assuming a steady state of growth for the business for eternity. This is called the Perpetuity Growth method, for which the formula can be seen below. | |
| − | + | ||
| − | + | ||
| − | + | <math> TV = \frac{FCF_N*(1-g)}{WACC-g} </math> | |
| − | + | where | |
| − | + | <math> FCF_N </math> is the final free cash flow in year N | |
| − | + | <math> g </math> is the growth rate | |
| − | + | The value that is calculated from this can be added onto the net present value to get a more realistic estimation. However, this method is highly dependant on unknown factors, meaning a lot of assumption will have to be made. This includes the growth rate and the calculated WACC. | |
| − | + | == Limitations == | |
| − | + | There are several limitations and issues when it comes to using the discounted cash flow method to try and value an investment. Most of these are caused by the fact that a lot of assumptions need to be made in order for the DCF to be used. | |
| + | One major flaw when it comes to both discounted cash flow and the net present value is that they both rely on forecasted estimates of costs and cash flows, and not actual measurable figures and numbers.<ref name="DCF" /> This means that both DCF and NPV will both result in estimates, which are only as good as the inputs and assumptions made, i.e. they are sensitive to the imputs made. <ref name="DCF2" /> | ||
| + | |||
| + | As the method is based on what happens in the future, sometimes 5-10 years away, everything becomes diffidult to forecast. The farther into the future, the more uncertain the numbers become, and therefore the DCF and NPV becomes more unreliable.<ref name="DCF" /> | ||
| + | |||
| + | Another limitation is that to allow for more precision, a lot of complexity will be introduced into the equations, for example in the free cash flow calculations, which were simplified for the purposes of this article. However, in reality it is not as simple to find the OPEX and CAPEX, and there are many other numbers that could be assessed.<ref name = "FCF" /> Furthermore, if aiming for precision of the model, it can only be as good as the forecasts of the future. This is all very well summed up in the phrase "Garbage in = Garbage out." | ||
| + | |||
| + | Furthermore, since projects are unpredictable by nature, it can be difficult to know when a return on the investment will start. This means that it can be very hard to predict future cash flows, which are needed to calculate the Discounted Cash Flow and the Net Present Value. <ref name="PMI" /> | ||
| + | |||
| + | Therefore, NPV and DCF should never be used as the sole reason for doing or not doing an investment in a project or a business. | ||
| + | |||
| + | == Annotated bibliography == | ||
| + | |||
| + | =====J.D Piante, 2014, The project as investment===== | ||
| + | This article from the Project Management Institute (PMI) discusses the value in considering projects as investments, and not just like investments. It also highlights the risks involved and the the return on investment. Furthermore, it also briefly mentions the downside of NPV, as it is very difficult to predict the future cash flows of a project. | ||
| + | |||
| + | ==== Investopedia.com, Discounted Cash Flow (DCF) Explained With Formula and Examples ==== | ||
| + | This article (Internet resource) explains what the discounted cash flow method is, along with examples of calculations. It also presents some limitations of the method, and how it should be used properly. As this is from a website, the credibility might not be as high as a published paper. However, it is an online based "newspaper" type platform formed in 1999, have won several awards and are transparent with their sources and writers. Overall a credible source, considering that it is from a website. Investopedia's articles has been used for more that just DCF for this wiki-page. All the uses can be seen in the references section. | ||
| + | |||
| + | ==== Bobbie Anne Munsey, 2023, What Are Operating Expenses? (With Types and Examples) ==== | ||
| + | This article (Internet resource) discusses what operating expences (OPEX) are and how they are used and assessed within company management. | ||
| + | |||
| + | ==== S. Brackenborough et al, 2001, THE EMERGENCE OF DISCOUNTED CASH FLOW ANALYSIS IN THE TYNESIDE COAL INDUSTRY ==== | ||
| + | This paper discusses the emergence of the discounted cash flow method in history, more specifically in the coal industry thorughout the 1700 hundreds. It highlights the origin of the method, and how it was a wealth-maximising analysis thoughout history. | ||
| + | |||
| + | == References == | ||
| + | <references> | ||
| − | ( | + | <ref name="RHPARKER">, "R.H. Parker, Discounted Cash Flow in Historical Perspective, 1968, Journal of Accounting Research" </ref> |
| + | <ref name="FCF">, "Free Cash Flow (FCF), https://groww.in/p/free-cash-flow" </ref> | ||
| + | <ref name="CAPEX">, "CapEx: Definition, Types and Examples, https://cbonds.com/glossary/capital-expenditure/" </ref> | ||
| + | <ref name="OPEX">, " Bobbie Anne Munsey, 2023, What Are Operating Expenses? (With Types and Examples), https://www.indeed.com/career-advice/career-development/operating-expenses" </ref> | ||
| + | <ref name="Compounding">, "Investing Basics: How Compound Growth Can Benefit Your Money, https://www.wellsfargo.com/financial-education/investing/compound-interest-growth/" </ref> | ||
| + | <ref name="TVM">, "Time Value of Money Explained with Formula and Examples, https://www.investopedia.com/terms/t/timevalueofmoney.asp </ref> | ||
| + | <ref name="NPV">, "Net Present Value (NPV): What It Means and Steps to Calculate It, https://www.investopedia.com/terms/n/npv.asp" </ref> | ||
| + | <ref name="WACC">, "Weighted Average Cost of Capital (WACC) Explained with Formula and Example, https://www.investopedia.com/terms/w/wacc.asp" </ref> | ||
| + | <ref name="DCF">, "Discounted Cash Flow (DCF) Explained With Formula and Examples, https://www.investopedia.com/terms/d/dcf.asp" </ref> | ||
| + | <ref name="DCF2">, "Discounted Cash Flow Analysis, https://www.streetofwalls.com/finance-training-courses/investment-banking-technical-training/discounted-cash-flow-analysis/" </ref> | ||
| + | <ref name="DiscountRate">," Discount Rate, https://www.wallstreetmojo.com/discount-rate/" </ref> | ||
| + | <ref name="PMI">, "J.D Piante, The project as investment, 2014, https://www.pmi.org/learning/library/project-investment-9384 </ref> | ||
| + | <ref name="Origin">, S. Brackenborough et al, 2001, THE EMERGENCE OF DISCOUNTED CASH FLOW ANALYSIS IN THE TYNESIDE COAL INDUSTRY c.1700–1820,The British Accounting Review </ref> | ||
| − | + | </references> | |
Latest revision as of 10:35, 9 May 2023
Developed by Oliver Skou Schwarz
This page refers to the discounted cash flow (DCF) method regarding projects and investments [1], which is used to evaluate if a project is worth pursuing based on its future financial merits.
Discounted Cash Flow often used to calculate and estimate the value of any investment or a project by projecting its future cash flows and then discounting them back to their present value (PV), meaning in todays money. [2]
The rationale behind the use discounted cash flow is that an investment in a project's value is equal to the sum of its forecasted future cash flows, discounted at an appropriate (often with lots of assumptions) rate. It is discounted due to the principle of the time value of money and the potential risk involved in the investment [2]. The time value of money refers to the tendency for money to lose its value over time. This sum of the all the discounted cash flows in a forecasted period is known as the Net Present Value (NPV).[2] Since the discounted cash flow is such a big part of the NPV, the two are almost interchangable when it comes to calculations.
[edit] Origin
The idea of discounted cash flow has been utilized in one way or another for many years, and can even be traced back to the coal industry in the 1700 hundreds [3]. However, The modern version trace back to the early 20th century, where it was used in finance and to analyse investments. One of the most influencial and modern uses of DCF was in 1930 by American economist Irving Fisher in "The Theory of Interest." Fisher used DCF to calculate the sum present value of future cash flows, which he coined the "net present value" of an investment.[4] Since then, this method has been widely used in valuation, including in finance, investment, and project management.
[edit] Math section
[edit] Formula
The discounted cash flow is a way of calculating the present value of a future free cash flow, evaluated at a given discount rate. That means any single given cash flow can be brought back to the value of the present. The formula for the DCF can be seen below.
Where
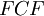 is a free cash flow.
is a free cash flow.
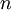 is the year in the forecasted period
is the year in the forecasted period 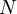 .
.
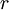 is the discount rate.
is the discount rate.
As the present value of a single cash flow is not that useful on its own, usually the formula is applied on a number of cash flows, corresponding to each year in a period. When done like this, the formula becomes a series of discounted cash flows added together. An example of this can be seen below.
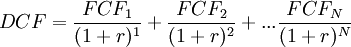
This can be used to assign value to a project or a business by assessing the cash flows it will generate within the forecasted period 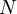 . Since the formula operates with increasing years, the further away in the future the cash flow is, the lower the present value of it will be. This is due to the time value of money.
. Since the formula operates with increasing years, the further away in the future the cash flow is, the lower the present value of it will be. This is due to the time value of money.
[edit] Discount Rate
The discounted cash flow formula is highly dependent on the discount rate 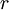 . The discount rate is a rate of interest which is applied to the future cash flows of an investment or a business, which determines the final Net Present Value (NPV). [5] There are several ways of determining the appropriate discount rate, but some level of uncertainty will always occur. For many intents and purposes, the discount rate is assumed to a certain value. However, for more precise values, there are ways of estimating it. Some of the most prevalent types of discount rate include[5] :
. The discount rate is a rate of interest which is applied to the future cash flows of an investment or a business, which determines the final Net Present Value (NPV). [5] There are several ways of determining the appropriate discount rate, but some level of uncertainty will always occur. For many intents and purposes, the discount rate is assumed to a certain value. However, for more precise values, there are ways of estimating it. Some of the most prevalent types of discount rate include[5] :
- Weighted Average Cost of Capital (WACC)
- Hurdle Rate
- Cost of Equity
- Cost of Debt
In this article, the WACC will be discussed in a later section.
[edit] Example
A simple example is given below. In this case, the DCF is only calculated for a single cash flow, 1 year from present. In this way, the result will be value of a cash flow a year from now in today's money. In this simple example, the business is a lemonade stand. The lemonade stand has a yearly total cost of 100$ and a yearly total revenue of 200$ in year 1. This will mean that the free cash flow (FCF) for year 1 is:
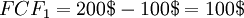
Now, it is assumed that there is a discount rate 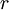 of 6%. With this, the final DCF for year
of 6%. With this, the final DCF for year 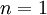 can be calculated as:
can be calculated as:
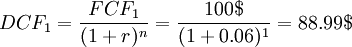
This means that even though the lemonade stand will generate 100$ next year, this is only worth 88.99$ today.
[edit] Application
This section highlights the application of DCF as well as important principles that are deeply connected to the method of discounting cash flows.
[edit] Time value of money
The time value of money (TVM) is an important concept that states that the value of money changes over time. Practically, this means that any sum of money today is worth more than the exact same amount of money in the future, and herefrom comes the well known expression "A dollar today is worth more than a dollar tomorrow." The reason behind this phenomenon is that money today has the potential and ability to be used to generate more money by investing them in clever ways, whereas money in the future can only be invested in the future, and thus loses its earnings potential (that is, for the present). Furthermore, factors like inflation and interest rates contribute to the fact that money can lose its value over time.[6] The time value of money is an then an extremely important principle in projects and especially when investing in them initially, as it helps project managers and coorporations make informed decisions about how to invest their resources smartly and which project to pursue. The TVM can be calculated both for present values and future values. The equation for future value (FV) can be seen below:
Where
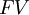 is the future value
is the future value
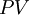 is the present value
is the present value
 is the interest rate
is the interest rate
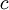 is the compoundings per year
is the compoundings per year
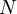 is the number of years
is the number of years
This equation can be used to estimate the value of a sum of money today in the future. It is highly dependent on the number of compounding periods per year. [7]
[edit] Free Cash Flow
The free cash flow (FCF) is the cash flow that is available after a business pays for the costs of continued operations, like operating expences and capital expenditures. Generally, the more free cash flow a business or a project has, the more attractive it will be for investors, as it will be able to invest in new opportunities. There are multiple ways of calculating the free cash flows depending on the level of precision and complexity desired. A simple model for calculating this can be seen below.
The sales revenue is the money going into the project or the business, hence the positive sign.
OPEX is the Operational Expenditure and it refers to the recurring short-term cost of maintaining the operations and keeping a project or a company running on a daily basis. This could be the cost of necessities such as rent, electricity, staff salaries, and other costs associated with delivering a project's desired outcome on a day-to-day scale. [9]
CAPEX is the Capital Expenditures, which refers to the amnount fo money a company or a project need to invest in acquiring its long-term assets needed to start operations. This can include assets such as property, equipment, or technology. [10] Capital Expenditures are generally more expensive and long-term than other expenses, such as the operational expenditure, and are considered investments in the company's future.
The Free Cash Flow is in this instance calculated for a single year. However, doing it for multiple years is necessary. Generally speaking, the FCF needs to be projected until it reaches a steady state (typically 5 to 10 years).[11]
[edit] Example
As the previous example mentioned, the free cash flow needed to be used in the DCF formula. However, the equation for finding the FCF for a lemonade stand was somewhat simplified. As can be seen from the equation for FCF, the free cash flow equals the total sales revenue (or other generated income) minus the total costs. However, this time the costs are divided into two categories. Operational costs and capital costs. Using the same numbers as the previous example, we have that the total sales revenue of the lemonade stand is 200$. The operational expenses are costs such as ingredients to make the lemonade (sugar, lemons, ice etc.). These are the things that are needed on a daily basis. On the other hand the capital expenses might be things like the actual stand and the sign - things that are invested in once in the beginning of the "venture."
We than have that:
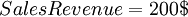
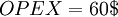
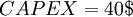
Putting it all into the formula, we get the same free cash flow for the first year as in the DCF example:
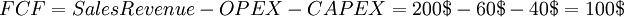
As this is just the free cash flow for one year, when calculating the NPV, cash flows for multiple years are required.
[edit] Net Present Value (NPV)
The Net Present Value (NPV) is another financial method that is used to evaluate the merits of project based on the discounted cash flow, and whether it is worth investing in. [12] It is often used to address the financial attractiveness of long-term investments, this could include a project like construction of new plant for a big production company. The value of the NPV would then tell something about the monetary value of the investent, and if it would generate a net loss or a net positive if made. NPV is extremely closely related to the discounted cash flow (DCF) as mentioned previously in the article, as it is merely the sum of all the discounted cash flows in a given forecasted period of time. This means that the formula and the method of calculation is almost identical to that of DCF. The formula for NPV can be seen below:
It is clear to see that this is identical to the DCF-formula, the only difference being the summation over all years in the time period 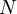 . This formula can then be used to decide whether a project is worth investing in.
. This formula can then be used to decide whether a project is worth investing in.
[edit] Net Present Value Rule
The net present value rule is a simple rule that can identify whether or not an investment should be made by companies and project managers, based on the estimated value of the NPV. The rule can be seen on the table below[12] .
| NPV = 0 | The investment will bring net zero value in present money terms. |
|---|---|
| NPV < 0 | The investment will result in a net loss. Investment should not be made. |
| NPV > 0 | The investment will result in a net gain. Investment should be made. |
This rule indicates that an investment should only be made (in monetary terms) if the net present value is positive.
[edit] Example
Now we make a new example of the lemonade stand, to see if it is worthwhile to invest in the lemonade stand. We assume that this will be over a 5 year period, meaning 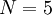 . On the following table the cash flow for each year can be seen (here we assume that the free cash flow has already been calculated, with sales and costs).
. On the following table the cash flow for each year can be seen (here we assume that the free cash flow has already been calculated, with sales and costs).
| Discount Rate | 6% |
|---|---|
| Initial Investment | 200$ |
| Year 1 | 60$ |
| Year 2 | 70$ |
| Year 3 | 40$ |
| Year 4 | 50$ |
| Year 5 | 60$ |
Note that the initial investment is considered now. This is the cost that is incurred in the present, i.e. the investment made in the business in year 0. Now we want to use the formula for NPV to see if the initial investment is worth it in the long run - that is the next 5 years.
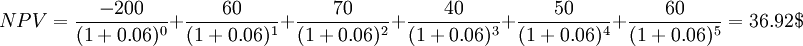
In this case, since we have a positive net present value of 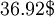 , it means that the lemonade stand is worth investing in. This essentially means that the stand makes this amount of money over the next 5 years, accounting for all costs.
, it means that the lemonade stand is worth investing in. This essentially means that the stand makes this amount of money over the next 5 years, accounting for all costs.
[edit] Working Average Cost of Capital (WACC)
The Weighted Average Cost of Capital (WACC) is a way of measuring the cost of financing for a company. This financing can come in two types: dept and equity. Both of these have an associated cost, that is relevant when calculating the WACC. As mentioned earlier, the WACC is often used as the discount rate in the formulas for DCF and NPV.[13] The formula for WACC can be seen below.
Where
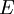 is the market value of the firm's equity
is the market value of the firm's equity
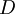 is the market value of the firm's dept
is the market value of the firm's dept
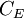 is the cost of equity
is the cost of equity
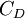 is the cost of dept
is the cost of dept
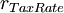 is the tax rate
is the tax rate
This formula can then be used to get a more precise estimation of the discount rate, and subsequently be used to calculate the discounted cash flow and the net present value.[13]
[edit] Terminal Value
The Terminal Value (TV) is the value of the firm or the project after the forecasted period. It is another important method that is used when trying to calculate the present value of a firm or an investment. As the discounted cash flow is done over a certain forecasted period, ususally a couple of years, the NPV of the company will be based only on the present values of the cash flows within this time period. However, in reality, companies keep going after the end of the forecasted period. This means that a company or the product of a completed project will still continue to generate cash flows after the forecasted period. The Terminal Value is then a technique used to capture all the cash flows that comes after the forecasted period and to infinity. This is done by assuming a steady state of growth for the business for eternity. This is called the Perpetuity Growth method, for which the formula can be seen below.
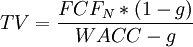
where
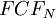 is the final free cash flow in year N
is the final free cash flow in year N
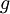 is the growth rate
is the growth rate
The value that is calculated from this can be added onto the net present value to get a more realistic estimation. However, this method is highly dependant on unknown factors, meaning a lot of assumption will have to be made. This includes the growth rate and the calculated WACC.
[edit] Limitations
There are several limitations and issues when it comes to using the discounted cash flow method to try and value an investment. Most of these are caused by the fact that a lot of assumptions need to be made in order for the DCF to be used. One major flaw when it comes to both discounted cash flow and the net present value is that they both rely on forecasted estimates of costs and cash flows, and not actual measurable figures and numbers.[2] This means that both DCF and NPV will both result in estimates, which are only as good as the inputs and assumptions made, i.e. they are sensitive to the imputs made. [11]
As the method is based on what happens in the future, sometimes 5-10 years away, everything becomes diffidult to forecast. The farther into the future, the more uncertain the numbers become, and therefore the DCF and NPV becomes more unreliable.[2]
Another limitation is that to allow for more precision, a lot of complexity will be introduced into the equations, for example in the free cash flow calculations, which were simplified for the purposes of this article. However, in reality it is not as simple to find the OPEX and CAPEX, and there are many other numbers that could be assessed.[8] Furthermore, if aiming for precision of the model, it can only be as good as the forecasts of the future. This is all very well summed up in the phrase "Garbage in = Garbage out."
Furthermore, since projects are unpredictable by nature, it can be difficult to know when a return on the investment will start. This means that it can be very hard to predict future cash flows, which are needed to calculate the Discounted Cash Flow and the Net Present Value. [1]
Therefore, NPV and DCF should never be used as the sole reason for doing or not doing an investment in a project or a business.
[edit] Annotated bibliography
[edit] J.D Piante, 2014, The project as investment
This article from the Project Management Institute (PMI) discusses the value in considering projects as investments, and not just like investments. It also highlights the risks involved and the the return on investment. Furthermore, it also briefly mentions the downside of NPV, as it is very difficult to predict the future cash flows of a project.
[edit] Investopedia.com, Discounted Cash Flow (DCF) Explained With Formula and Examples
This article (Internet resource) explains what the discounted cash flow method is, along with examples of calculations. It also presents some limitations of the method, and how it should be used properly. As this is from a website, the credibility might not be as high as a published paper. However, it is an online based "newspaper" type platform formed in 1999, have won several awards and are transparent with their sources and writers. Overall a credible source, considering that it is from a website. Investopedia's articles has been used for more that just DCF for this wiki-page. All the uses can be seen in the references section.
[edit] Bobbie Anne Munsey, 2023, What Are Operating Expenses? (With Types and Examples)
This article (Internet resource) discusses what operating expences (OPEX) are and how they are used and assessed within company management.
[edit] S. Brackenborough et al, 2001, THE EMERGENCE OF DISCOUNTED CASH FLOW ANALYSIS IN THE TYNESIDE COAL INDUSTRY
This paper discusses the emergence of the discounted cash flow method in history, more specifically in the coal industry thorughout the 1700 hundreds. It highlights the origin of the method, and how it was a wealth-maximising analysis thoughout history.
[edit] References
- ↑ 1.0 1.1 , "J.D Piante, The project as investment, 2014, https://www.pmi.org/learning/library/project-investment-9384
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 , "Discounted Cash Flow (DCF) Explained With Formula and Examples, https://www.investopedia.com/terms/d/dcf.asp"
- ↑ , S. Brackenborough et al, 2001, THE EMERGENCE OF DISCOUNTED CASH FLOW ANALYSIS IN THE TYNESIDE COAL INDUSTRY c.1700–1820,The British Accounting Review
- ↑ , "R.H. Parker, Discounted Cash Flow in Historical Perspective, 1968, Journal of Accounting Research"
- ↑ 5.0 5.1 ," Discount Rate, https://www.wallstreetmojo.com/discount-rate/"
- ↑ 6.0 6.1 , "Time Value of Money Explained with Formula and Examples, https://www.investopedia.com/terms/t/timevalueofmoney.asp
- ↑ , "Investing Basics: How Compound Growth Can Benefit Your Money, https://www.wellsfargo.com/financial-education/investing/compound-interest-growth/"
- ↑ 8.0 8.1 , "Free Cash Flow (FCF), https://groww.in/p/free-cash-flow"
- ↑ , " Bobbie Anne Munsey, 2023, What Are Operating Expenses? (With Types and Examples), https://www.indeed.com/career-advice/career-development/operating-expenses"
- ↑ , "CapEx: Definition, Types and Examples, https://cbonds.com/glossary/capital-expenditure/"
- ↑ 11.0 11.1 , "Discounted Cash Flow Analysis, https://www.streetofwalls.com/finance-training-courses/investment-banking-technical-training/discounted-cash-flow-analysis/"
- ↑ 12.0 12.1 12.2 , "Net Present Value (NPV): What It Means and Steps to Calculate It, https://www.investopedia.com/terms/n/npv.asp"
- ↑ 13.0 13.1 13.2 , "Weighted Average Cost of Capital (WACC) Explained with Formula and Example, https://www.investopedia.com/terms/w/wacc.asp"