Revision as of 19:10, 7 October 2015

Introduction

The network-based analysis enables design and planning of a project, at all levels of details, regarding the duration of each activity, the order of priority, the review of the program when changes or delays happen and finally the cost of the project.

The methods of network-based analysis which are used to optimize the design and planning of a project are Program Evaluation and Review Technique (PERT) and Critical Path Method (CPM) . These methodologies were developed independently of each other in late 50s. Researchers have used PERT method for handling problems with stochastic activities' times while they have used CPM for problems with deterministic times.

Essentially, this difference resulted because these two methods encountered problems of different nature during the period they were developed. There were also differences in the way in which the two methods depicting activities with a network form.

In PERT networks, the activities were represented with edges while in CPM networks, the nodes symbolized the activities.

In any case, these differences do not exist anymore. The way of representation of the activities is based on the user's selection while the methodology is merged in a common method which is called PERT/CPM method. According to this, all the networks which are obtained by this method, they are called PERT/CPM networks.

History

In 1958, James E. Kelly of Remington Rand and Morgan R. Walker of DuPont, apply for the first time the CPM to support the planning of construction and maintenance of industrial chemical production complexes. The cases of use of CPM are presented mainly in construction works, in construction of airplanes and in large shipbuilders.

Application

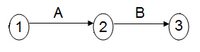
PERT/CPM network representation

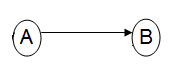
There are two methods for representing the PERT / CPM networks.

alt text

The first method is the Activity On Arrow (AOA) where each activity is represented by a unique edge, whereas the nodes represent the starting and finishing events of the activity which is enclosed by the edge defined by two nodes. In a PERT / CPM network, the lengths of the edges are not necessarily proportionate to the duration of each activity. The relative sequence of the activities is reflected by the fact that the starting node of an activity, i.e. an edge which starts at a node, can be both the finishing node of other activities (edges) that lead to it. So, all the activities which are leaded to a node must be completed before starting an activity whose edge starts from the same node. In each edge it is noted the symbol of the corresponding activity and its duration. This representation is called PERT / CPM network on an AOA type.

alt text

The second method is the Activity On Node (AON) where each activity is represented by a single node. The relation of sequence is reflected by the edges which connect the nodes-activities. Each activity (node) which is associated with a subsequent activity through an edge is a prerequisite and must be completed before starting the next activity. At each node we note the duration and the name of the corresponding activity. This representation is called PERT/CPM network on an AON type.

Project planning under uncertainty

Usually in applying the PERT/CPM method, it is assumed that the process time of each activity is known and predetermined with the maximum possible accuracy. However, there are cases where the duration of each activity is not known. This happens mainly in projects where there are activities which are executed for the first time and there is no sufficient knowledge about the expected time that is needed for an activity to be completed. Because in these cases there are variations in the duration of the activities, the duration is considered as random variable. So, the theory of probability is used to analyze the project, and to obtain information. There are three needed information for each activity and they concern estimations of the expected duration as it follows:

1. Optimistic time: According to estimations, it is the shortest time that an activity lasts. In other words, it is the required time for the execution of an activity under ideal conditions. This happens only if any delay problem is occurred. It is represented with an α.

2. Pessimistic time: According to estimations, it is the larger time that an activity lasts. In other words, it is the required time for an execution of an activity under the worst possible conditions, i.e. if presented many problems of delay in implementation of it. It is represented with a b.

3. Most-likely time: It is the most common rate of the time, which is taken for an activity to be completed and it is considered as the required time for the execution of an activity under normal conditions. It is represented with an m.

alt text

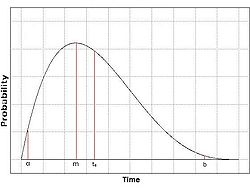
In order the variability that exists in the execution times of each activity to be described, the beta distribution is usually used. This distribution has some special characteristics that facilitate the assessment of the expected time 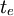$\begin{align} t_{e} \end{align}$ that an activity lasts. In principle, the curve of this distribution is unimodal, i.e. it is a single peak distribution and it is ascending from the left side and descending at the right side. It is adapted to the values of α, b and m, and may be symmetrical or skewed to the right or to the left. The highest point of the curve corresponds to the m value. The average and the variance can be easily accessed with formulas that use the three assessments α, b and m. 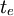The figure on the right, shows a curve of the beta distribution, in which the three assessments α, b and m, and also the expected value $\begin{align} t_{e} \end{align}$ are clearly distinguished. As shown in the same figure, the peak of the curve corresponds to the most-likely time m, while the two ends α and b correspond to possible but extreme cases. 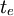The average $\begin{align} t_{e} \end{align}$ divides the area beneath the curve in two equal portions. Thus, the probability of an activity to last less or equal of the average value is 50%, as well as the probability lasting a time greater than 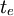$\begin{align} t_{e} \end{align}$ . On occasions where the curve of the beta distribution is symmetrical, the most-likely time m will be equal to the average 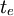$\begin{align} t_{e} \end{align}$ . When we have the three estimates α, b and m for the duration of each activity, which are provided by the relevant managers, then the following equation (1) to calculate the expected duration can occur.

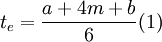
$\begin{align} t_{e}=\frac{a+4m+b}{6} (1) \end{align}$

The variation of time for each activity, describes the variability that exists during each activity and is approached by the following equation (2):

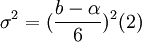
$\begin{align} \sigma^2 = (\frac{b- \alpha}{6})^2 (2) \end{align}$

The standard deviation of the time is given by the following equation (3):

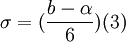
$\begin{align} \sigma = (\frac{b- \alpha}{6}) (3) \end{align}$

The value of the variation is depended on the distance of the two extreme values of the time, the pessimistic (b) and the optimistic (α). The relations (2) and (3) apply only if an assumption is made that the random variable expressing time, follows the beta distribution.

When the durations of activities are stochastic, then the PERT / CPM method is applied. In such cases, the expected times of the equation (1) are used for the calculations of times ES, EF, LS, LF. Also from the equation (2) the variation of the time for each activity is calculated, while for each path, the total duration of the activities that compose it, the anticipated prices of their times can be found. So, for each path the total expected time can be calculated. It is also very significant the total time of the critical path, which is an estimation of the average of the total project completion time. The critical path can be identified based on the expected values from the relationship (2), and then the expected total time of the work to be estimated. Simultaneously, it is important to calculate the variance of the time of the critical path, since this is an indicator of the variation of the duration of a project. The fluctuation of the time that lasts the whole activities is given by the sum of the variations of activities that compose it by the following equation (4):

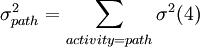
$\begin{align} \sigma^2_{path}=\sum\limits_{activity=path}\sigma^2 (4) \end{align}$

where 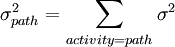$\begin{align} \sigma^2_{path}=\sum\limits_{activity=path}\sigma^2 \end{align}$ is the summary of all the activities of this pathway. Therefore, if in the equation (4), the activities of the critical path are calculated, the variance of the total time of the project is estimated. The standard deviation of the time is the outcome from the square root of the equation (4).

A very important element of the analysis is the "total duration of the project”. It is a random variable, which can be considered to follow the normal distribution, with average the sum of the expected values and the duration of the activities on the critical path and variance the sum of these variations of these durations. The thoughtfulness behind the project completion time, leads to another level of stochastic analysis of the problem. As is apparent from the above, it is not known for how long the project will last before it is completed, but it is known that the normal distribution with known parameters. In such cases, it is possible to calculate the probability of completing the project within a given time. This calculation is based on the assumption that the total time of the project follows the normal distribution which means that the values of time integration of individual activities is statistically independent, that there is a quite large variety of activities and that the paths which are created, they are also independent.

The planning of a project, whose duration times of the activities are thoughtful, can be divided into two main sections. The first section is calculated using the three estimates for each activity (optimistic, pessimistic, and most-likely time), the expected duration of each of them and the variance or the standard deviation of this duration. Using the expected values, the PERT / CPM method is applied to calculate times ES, EF, LS and LF, to identify the critical path, the ST times and the total expected project completion time. For all of these expected values which are estimated, the corresponding variations and standard deviations can be calculated. If the conditions that were reported are applied, then the total duration of the project, which is a random variable, follows the normal distribution with known mean and deviation. Thus, the second part of the analysis which is related to the finding of the possibility follows in order to complete the task in a given time. This last part is, as the reader perceives, extremely important in the overall analysis of the project, because when there is uncertainty about the durations of activities, it is critical to know the success rate which is associated with the completion of the project within a specific time horizon.

Program review and time compression

Example

Exercise

Solution

Usage

Discussion

The key questions that can be answered and moreover the general the information which can be acquired by the project manager and by extension, the execution group by constructing the PERT/CPM network are the followings:

The graphical representation of the activities and in particular, accurate graphical representation of the sequence of prerequisite activities.
The estimation of the total time that the work will last.
The identification of the critical activities. In other words, all these activities that must not be delayed because then, the completion of the project will be delayed.
The identification of non-critical activities. In other words, all these activities which have delay margins without affecting the project.
For each non-critical activity, the slack time can be detected. In other words, this is the maximum possible margin delay of an activity without charge of the total time of the project.
The identification of the probability of the project completion within a certain period of time and in particular in cases where the duration times of activities are estimations.
The ability to monitor the temporal evolution of the project, the allocation of resources and the possibility of revising the program by changing times, identifying new critical activities and reallocating resources.
The definition of the possibility to reduce the project completion time (crashing), by the determination of the required resources and the activities which need to be fed.

Advantages

Limitations

References

PERT/CPM

Revision as of 19:10, 7 October 2015

Contents

History

Application

PERT/CPM network representation

Project planning under uncertainty

Program review and time compression

Example

Exercise

Solution

Usage

Discussion

Advantages

Limitations

Related Articles

References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox

@@ Line 96: / Line 96: @@
 \end{align}
 </math>
-means the summary of all the activities of this pathway. Therefore, if in the equation (4), the activities of the critical path are calculated, the variance of the total time of the project is estimated. The standard deviation of the time is the outcome from the square root of the equation (4).
+is the summary of all the activities of this pathway. Therefore, if in the equation (4), the activities of the critical path are calculated, the variance of the total time of the project is estimated. The standard deviation of the time is the outcome from the square root of the equation (4).
 A very important element of the analysis is the "total duration of the project”. It is a random variable, which can be considered to follow the normal distribution, with average the sum of the expected values and the duration of the activities on the critical path and variance the sum of these variations of these durations. The thoughtfulness behind the project completion time, leads to another level of stochastic analysis of the problem. As is apparent from the above, it is not known for how long the project will last before it is completed, but it is known that the normal distribution with known parameters. In such cases, it is possible to calculate the probability of completing the project within a given time. This calculation is based on the assumption that the total time of the project follows the normal distribution which means that the values of time integration of individual activities is statistically independent, that there is a quite large variety of activities and that the paths which are created, they are also independent.