The Critical Path Method in project planning
(→Time-Cost Trade-Off) |
(→Time-Cost Trade-Off) |
||
| Line 133: | Line 133: | ||
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | ||
| − | |+ Table 2: Information for | + | |+ Table 2: Information for Time-Cost Trade-Off calculation. |
|- | |- | ||
! Activity | ! Activity | ||
Revision as of 22:33, 15 September 2016
The Critical Path Method is a step by step technique that is used to schedule a set of project activities. It analysis what activities are least flexible and the project duration is predicted based on the activities that fall along the critical path. The critical path is the longest sequence of activities in a project plan which must be completed on time in order for the project to complete on the predetermined scheduled date [1]. By delaying an activity on the critical path leads to a delay on the completion time of the entire project as these activities have no slack. Activities along the path cannot start until the predecessor activity is completed. When using CPM to plan a project a graphical diagram is often represented showing how each activity is related to the others [2]. This method is one of several tools that is important to keep the project on track and is convenient for all forms of projects, including research projects, product development, construction industry, maintenance and many more.
A joint venture between the Dupont chemical company and computer firm Remington Rand Univac led to a development of the Critical Path Method in the 1956 to tackle the interrelationships of separate activities within a project schedule [3].
In this article the Critical Path Method (CPM) is described, a step by step guidance on how to apply the method is discussed and the tradeoff between cost and time are analyzed. Furthermore, a comparison to other project management techniques is performed and its limitations and advantages are addressed.
Contents |
Overview
Introduction and purpose of CPM
History
General methodology
Application
CPM graph box layout
CPM network creation
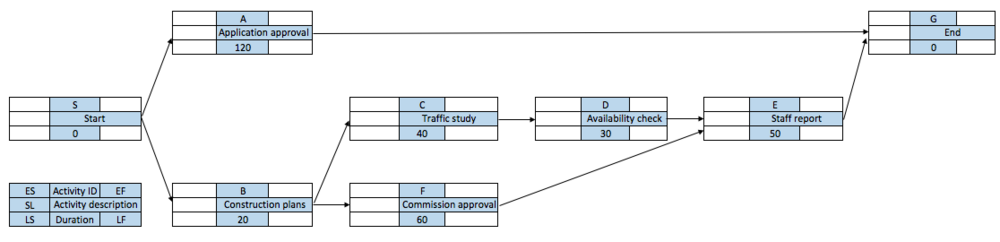
The first step in CPM analysis is constructing CPM network, which is developed from the WBS. The network is a visual flow diagram of the sequence, interrelationship, and dependencies of all the activities that must be accomplished to complete the project. The network is built using nodes and arrows, where the node represents an activity and the arrow shows dependency and project flow. http://www.engr.sjsu.edu/fayad/current.courses/cmpe203-fall2013/docs/Articles/Project%20Management%205th%20Edition.pdf
Basic rules that apply in general when developing a project network are as follow: http://www.engr.sjsu.edu/fayad/current.courses/cmpe203-fall2013/docs/Articles/Project%20Management%205th%20Edition.pdf
- Networks flow from left to right
- All preceding connected activities must be completed before the following activity can begin
- Arrows can cross over each other
- Each activity should have a unique ID code
- An activity identification number must be larger than that of any activities that precede it
- Recycling through a set of activities cannot occur
- Conditional statements are not allowed
A CPM network diagram can be constructed given the following information: A list of all activities involved in a project and their description, a list of its precedences for each activity and lastly a list of the duration of each activity. Table 1 is an example of a list of activities that will be used to construct CPM network diagram. http://www.engr.sjsu.edu/fayad/current.courses/cmpe203-fall2013/docs/Articles/Project%20Management%205th%20Edition.pdf
| Activity | Description | Preceding Activity | Duration [day] |
|---|---|---|---|
| |
Application approval | |
|
| |
Construction plans | |
|
| |
Traffic study | |
|
| |
Availability check | |
|
| |
Staff report | |
|
| |
Commission approval | |
|
Figure 4 shows the network with the activity time estimates found in the nodes. For example, activity A has an activity duration of 120 workdays, and activity C has an activity duration of 30 days. These informations are used in the next step called forward pass.
Forward pass
The second step is to calculate the ES, EF and expected normal completion time (TE) by using forward pass computation. This process requires that each path is traced through the network to the last project activity. The longest path denotes the project completion time for the plan and is called the critical path (CP). There are three steps that need to be kept in mind when using forward pass: http://www.engr.sjsu.edu/fayad/current.courses/cmpe203-fall2013/docs/Articles/Project%20Management%205th%20Edition.pdf
- Activity times are added along each path in the network: ES + DUR = EF.
- The EF is carried to the next activity where it becomes its ES. However, there is one exception which is,
- If the next succeeding activity is a merge activity (activity that has more than one predecessor), the largest EF of all its immediate predecessor activities is selected.
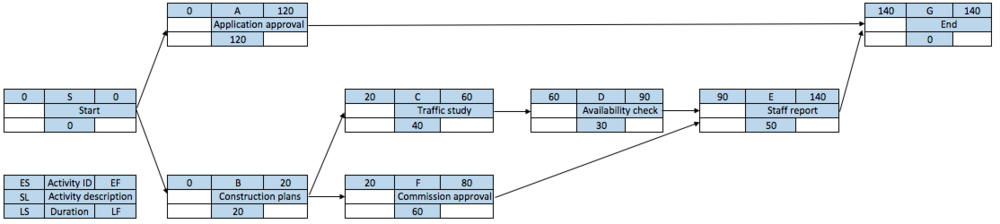
The forward pass begins with the project early start time (ES), which is 0 in this example (activity A and B). This time is found in the upper left corner of the activity nodes in Figure 5. The early finish for activity A is 120 = 0+120 (ES + DUR = EF). The same formula is used to calculate EF for activity B, which resulted in 20. Next, it can be seen that activity B is the predecessor for activities C and F. Therefore, the earliest these activities can begin is when activity B is completed. Using the formula mentioned here above the EF can be calculated for all the activities. It is important to note that since activity E is a merge activity then EF of activities D and F must be viewed due to the reason that they are both immediately preceding activity E in order to be able to find ES for E. Because activity D has higher EF that activity F it controls the ES of activity E, therefore ES for activity E is 90. The EF for activity E is 140, which is the earliest the project can be expected to complete(TE) under normal conditions. Now since ES, EF and TE is known the next step is to move to the backward pass process.
Backward pass
The third step, the backward pass is similar to the forward pass, except for it requires that the start point is from the last project activity(ies) and each path is traced backward to find LS and LF for each activity. There are three things that are important to keep in mind when using the backward pass process: http://www.engr.sjsu.edu/fayad/current.courses/cmpe203-fall2013/docs/Articles/Project%20Management%205th%20Edition.pdf
- Activity times are subtracted along each path starting with the project end activity: LF – DUR = LS.
- LS is carried to the next preceding activity to establish its LF. However, there is one exception, which is
- If the next preceding activity is a burst activity (activity that has more than one successor), the smallest LS of all its immediate successor activities is selected to establish its LF.
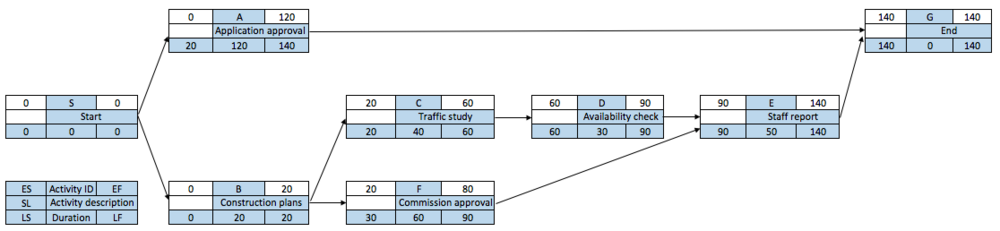
Before the backward pass can be computed, LF for the last activity(ies) must be selected. This time is usually set to equal to EF of the last activity. In case of multiple finish activities, the activity with the largest EF is chosen as LF, however when an imposed project duration deadline exist that date will be used. In this example the LF is set to be equal to LS of activity E, which is 140. The LS for activity E is 90 (LF –DUR = LS, 140 – 50 = 90). The late start for activity E becomes the LF for activity D, which is 90. By using the formula mentioned in this section LS can be calculated for all activities. When activity B has been reached it can be seen that it is a burst activity since it has more than one successor. The LF of activity B is controlled by the LS of activities C and F. According to rule no. 3 the smallest LF should be selected. LS of activity C is 40 and LS of activity F is 60, therefore LS of activity C becomes LF of activity B. The latest activity B can finish is 20 days. Once the LS for activities A and B have been calculated the backward pass is completed and the latest activity time is known (A: 140 – 120 = 20, B: 20 – 20 = 0). The solution of the calculation can be seen in Figure 6.
Slack calculation
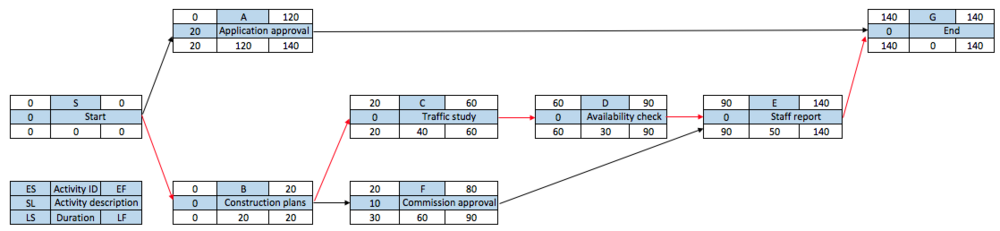
After the computation of the forward and backward pass, it is possible to determine the slack (SL) for each activity. By computing the SL, it is possible to determine which activities can be delayed and how much without delaying the project. The total slack is the difference between the LS and the EF (LS – ES = SL) and between the LF and EF (LF – EF = SL). For example, in Figure x the SL for activity F is 30 – 20 = 10. This means that activity F can be delayed by 10 without delaying the whole project. If the SL of one activity is used, the ES for all activities that follow in the chain will be delayed and their slack reduced.
The critical path can be identified after after the computation of the SL for each activity. Activities that have zero slack belong to the critical path. As can be seen in Figure 7, the activities on the critical path are B, C, D and E. Delay of any of these activities will delay the total project by the same number of days.
Time-Cost Trade-Off
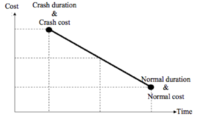
The aim of the time-cost trade-off analysis is to reduce the original project duration, determined from the CPM, to meet a specific deadline, with the least cost. In general, there is a trade-off between the time and the direct cost to complete an activity, the less expensive the resource the larger duration they take to complete an activity. Shortening the duration on an activity will normally increase its direct cost. A simple version of the relationship between the duration of an activity and its direct cost can be seen in Figure 8. The normal cost is the least direct cost required to complete an activity, and the corresponding duration is called the normal duration. The crash duration is the shortest duration required to complete the activity and the corresponding cost is called the crash cost. http://osp.mans.edu.eg/elbeltagi/CM%20CH8%20Time-Cost.pdf
To solve the time-cost trade-off problem several heuristic approaches can be used, such as the cost slope method. The step by step procedure for that method is summarised as follow: http://osp.mans.edu.eg/elbeltagi/CM%20CH8%20Time-Cost.pdf
- Apply the CPM technique as mentioned in the Application section to identify the critical path.
- Compute the cost slope for each activity by applying following equation: Cost slope = (crash cost – normal cost) / (normal duration – crash duration).
- Shorten the activity duration on the critical path that has the least cost slope and has not been shortened to its crash duration.
- Keep reducing the duration of the activities on the critical path that have the lowest cost slope until its crash duration is reached or until the critical path changes.
- In some cases, multiple critical paths are involved. The activity(ies) to shorten is determined by comparing the cost slope of the activity on all critical paths with the sum of cost slope for a group of activities.
- Once a critical path is shortened the duration of the activities and the slack should be adjusted.
- The cost increase is calculated by multiplying the cost slope with the shortening time of the activities.
- This heuristic approach should be continued until no further shortening is possible and the crash point is reached.
To get a deeper understanding of how application of this method works a detailed example will be shown in here below.
Example of the time-cost trade-off calculation
The example of this computation was retrieved from…. http://osp.mans.edu.eg/elbeltagi/CM%20CH8%20Time-Cost.pdf
The aim is to crash the project duration to 110 days. As mentioned in the Application section, the normal project duration is 140 days and the critical path is B-C-D-E. Project total normal cost is the sum the normal cost in Table x, which is 48.300.
| Activity | Description | Preceding Activity | Normal duration [day] | Normal cost | Crash duration [day] | Crash cost |
|---|---|---|---|---|---|---|
| |
Application approval | |
|
|
|
|
| |
Construction plans | |
|
|
|
|
| |
Traffic study | |
|
|
|
|
| |
Availability check | |
|
|
|
|
| |
Staff report | |
|
|
|
|
| |
Commission approval | |
|
|
|
|
The cost slope in Figure x is calculated by inserting relevant values into the cost slope equation. For example, for activity C the cost slope is (22,000-16,000) / (40-30) = 600. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must then be adjusted.
There are several project management techniques that are related to CPM, e.g. Project Management and Review Technique(PERT) and Critical Chain Method(CCM). These methods are used for management of projects with the aim to finish on time and within budget. Nevertheless, there are many differences between all these methods which will be discussed in this section.
CPM and PERT are often used in conjunction with each other to manage projects in a successful way. One of their differences is that PERT is a project management technique where planning, scheduling, organising, coordinating and controlling of uncertain activities is done, while CPM is a statistical technique of project management in which planning, scheduling, organising, coordination and control of well-defined activities takes place. Another difference is that PERT is a technique of planning and control of time while CPM is a method to control cost and time. Furthermore, the focus is in events when PERT is applied. Unlike CPM, where the focus is on activities. Lastly, to shorten project duration with least additional cost a cashing technique can be applied to CPM, however the crashing concept is not applicable to PERT. There are many more differences between these methods which will not be discussed further in this article. [4]
Moving on to the CCM which is built on CPM. Both methods are “Critical” and as their name suggest there are similarities and differences among the two of them. The main differences are that CPM involves the calculation of ES, EF, LS, LF and SL through forwards and backward passes in the project and focuses on the sequence of activities and the estimated duration of individual task in a straight forward manner. Task buffers are added to each task. On the other hand, CCM just put tasks together in a chain by considering the minimal time needed for individual tasks. An overall project buffer is combined to the end of the project chain. [5]
Advantages and disadvantages/limitations of CPM
CPM tool has proved to be very valuable and beneficial when it comes to managing projects. Advantages of using this method are many and the list could get rather long. Listed here below are few of the advantages that organisations could gain by using CPM: [6] [7]
- The greatest advantage of CPM can be seen in the planning stage, were the user is required to think through a project logically and with sufficient detail to establish form, clear project objectives, activities and specification. This helps preventing the chance of overlooking necessary activities and goals of a project.
- CPM provides a realistic and disciplined method for determining how to attain the project objectives and for communicating and documenting the project plans, schedules, time and cost performance clearly and concisely in the scheduling stage, where a time chart is constructed for each activity.
- In the monitoring stage, CPM identifies the most critical elements in the plan making the managers focusing on the activities that are most constraining on the scheduling. CPM will generate new schedules when there are changes in the durations of the activities. And as technical or procedural changes are considered, CPM provides an easy method for evaluating the effects these changes have on the overall project schedule.
Moving on the disadvantages and limitations of CPM. As for most of the management methods available, CPM faces several disadvantages and limitations, mainly as result of the technical and conceptual factors involved in the Critical Path Analysis(CPA) process. The below list include few of the advantages and limitations of CPM: [8] [9] [10]
- CPM can become extremely complicated and the complexity increases as the scope and extent of big projects increase. The risk of making a mistake in the calculation of the critical path becomes very high. If projects are not well defined CPM can become ineffective and difficult to manage.
- Does not take scheduling of personnel and resource allocations into account.
- It requires software to monitor the plan in bulky and lengthy projects.
- Critical path of a big project has to be calculated carefully since it is not always clear. In big projects CPM takes longer to identify and monitor the critical path. In many cases the critical paths might change and past critical paths may no longer be valid. This requires that the managers have to constantly review the network diagram and identify the changes occurred over the time.
- CPM operates on the assumption that there is a precise known time that each activity in the project will take, but that is not always the case in real practice.
- The time estimates of CPM are not based on statistical analysis.
- CPM cannot be used as a dynamic controlling device.
Conclusion
References
- ↑ Critical Path, BusinessDictionary, 2016.
- ↑ Critical Path Method, webopedia, 2016.
- ↑ History of the Critical Path Method, Kielmas, Maria, 2016.
- ↑ Surbni, S. (2015). Differences Between PERT and CPM. Retrieved September 5, 2016, from http://keydifferences.com/difference-between-pert-and-cpm.html#Definition.
- ↑ Chung, E. (2016). Critical Path Method vs Critical Chain Method for PMP Exam. Retrieved September 5, 2016, from http://edward-designer.com/web/critical-path-method-vs-critical-chain-method-for-pmp-exam/.
- ↑ Anderson, E. B. & Hales, S. T. (1986). Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES). Pp. 1-2. Retrieved September 8, 2016, from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.115.6122&rep=rep1&type=pdf.
- ↑ Advantages of Critical Path Method (CPM). Retrieved September 8, 2016, from http://theconstructor.org/construction/const-management/scheduling/advantages-of-critical-path-method-cpm/6873/.
- ↑ Stealth, P. & Roy, G. L. (2009). Project’s Analysis through CPM (Critical Path Method). Pp. 23-25. Retrieved September 8, 2016, from http://www.iiuedu.eu/press/journals/sds/sds1_july_2008/05_SECC_01.pdf.
- ↑ Advantages and disadvantages in the implementation of CPM. Retrieved September 8, 2016, from http://www.cpmscheduling.com/critical-path-method/advantages-and-disadvantages-in-the-implementation-of-cpm.
- ↑ Sinha, DK. (2015). Critical Path Method(CPM): Definition, Advantages and Limitations. Retrieved September 8, 2016, from http://www.yourarticlelibrary.com/business/planning-business/critical-path-method-cpm-definition-advantages-and-limitations/40754/.