The Critical Path Method (CPM) in Project Management
(→Methodology) |
(→Methodology) |
||
| Line 101: | Line 101: | ||
<b>Step 4: Critical Path Identification</b> | <b>Step 4: Critical Path Identification</b> | ||
| + | |||
The '''critical path''' is of great importance since all '''critical activities''' must be completed as scheduled in order to meet the scheduled project completion time, that is, if an activity on the '''critical path''' is delayed, the project is delayed by the same amount of time. This is due to the fact that the activities on the '''critical path''' have a '''zero slack'''. '''Slack (SL)''' is defined as the amount of time an activity can be delayed without delaying the whole project. Therefore, project managers need pay close attention to the critical path activities in order to ensure that they are not delayed and therefore put the entire project in the risk of being late. | The '''critical path''' is of great importance since all '''critical activities''' must be completed as scheduled in order to meet the scheduled project completion time, that is, if an activity on the '''critical path''' is delayed, the project is delayed by the same amount of time. This is due to the fact that the activities on the '''critical path''' have a '''zero slack'''. '''Slack (SL)''' is defined as the amount of time an activity can be delayed without delaying the whole project. Therefore, project managers need pay close attention to the critical path activities in order to ensure that they are not delayed and therefore put the entire project in the risk of being late. | ||
<b>Step 4: Update of project pogress</b> | <b>Step 4: Update of project pogress</b> | ||
| + | |||
| + | FAFAFAF | ||
== CPM Example == | == CPM Example == | ||
Revision as of 15:58, 16 September 2016
According to the Project Management Institute (PMI), project management is the application of knowledge, skills, tools and techniques to project activities in order to meet project requirements and objectives.[1] The challenging task of managing projects can be supported by an operation reserach technique called the Critical Path Method (CPM). The CPM is a mathematically-network based algorithm in which can be used for planning, scheduling and monitoring project progress. [2]
The technique developed in late 1950s utilizes information from a work breakdown structure (WBS) in a network representation to display interrelationships and dependencies between project activities that must be accomplished to complete a project. The technique is used for analyzing projects by determining the longest sequence of tasks through a project network, called the critical path. This determines the shortest possible time to complete the project as well as which activities should be of particular focus within the project.[3]
Based on acquired information from the CPM, the next question could be if it is possible to shorten the project in order to finish within certain deadline and what is the least expensive way to do it. In today’s competitive environment, there is an increasing pressure to get projects done earlier and quicker, either from the very beginning, prior to setting the project baseline or in the midst of project execution, to get the project back on schedule. Comparison of the benefits by reducing project time with the total cost associated with it can often be a huge challenge for project managers, thus, the decision to reduce the project duration must be based on an analysis of the trade-offs between time and cost.[2][4]
Contents |
Overview
Introduction
Organizations across the world and within different sectors have been using project management as a way to improve project results. The increased awareness and acceptance supports that the application of knowledge, skills, tools and techniques can have significant impact on project success.[5][1]
According to the ISO 21500 a project is defined as a “unique set of processes consisting of coordinated and controlled activities with start and end dates, performed to achieve project objectives. Achievement of the project objectives requires the provision of deliverables conforming to specific requirements.” [7]
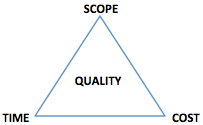
Each and every project is carried out under certain constraints. The three constraints of cost, time and scope represent together the iron triangle of project management, which can be seen in Figure 1. Each constraint forms the vertices with quality as the central theme and together indicates that projects must be delivered within agreed time and cost and furthermore to meet the agreed scope and customer quality requirements. The three constraints are aligned and changes in one will likely affect the others, or impact the quality of the project. This emphasizes the importance of project management and its challenging area in which is not at all easy to deal with.[6][8]
Project management is accomplished through the appropriate application of five processes: [1]
- Iniating
- Planning
- Executing
- Monitoring and Controlling
- Closing
Each and every organization can be involved in a project of any size, duration and complexity level at any given time. It is notable that project planning, scheduling and monitoring is a major part involved in project management. Therefore the critical path method (CPM) can be of good support within the challenging process of managing projects and helps those involved to address questions such as: [9]
- What is the (minimum) total time required to complete the whole project?
- What are the (earliest and latest) start and completion times for individual activities in the project?
- Which activities are critical and must be completed on time in order to complete the whole project on time?
- How much delay is tolerated of non-critical activities without impacting the overall project schedule and project completion time?
- With cost information on each activity: What is the least expensive way to reduce project duration in order to meet a targeted completion time?
All these questions are extreamly valid and important to have under control when managing projects.
Background
The critical path method (CPM) is a mathematically-network based project modeling technique developed in late 1950s in order to plan, schedule and control large, complex projects with many activities. CPM is one approach of network techniques that has been widely used and was developed by a DuPont engineer Morgan R. Walker and a Remington Rand computer expert, James E. Kelly, Jr. to manage plant maintenance and construction work. Furthermore, PERT (Program Evaluation and Review Technique), a critical path network technique was developed simultaneously and independently from the CPM by the U.S. Navy for managing the Fleet Ballistic Missile (Polaris) submarine project. PERT is commonly used in conjunction with CPM and the two optimization techniques are often referred to collectively. [4][10][11]
The CPM technique has been used for many different forms of projects including construction of a new building, bridge or a road, construction of IT-systems, building of ships and research and development of new products. As can be imagened, these projects consist of multiple activities that have to be completed in order to finish the whole project. It is important to note that the methodology is normally not applied to real large scale and complex problems with many activities, since developing the project network and applying the technique can be extremely time consuming. Today, there exists project management software packages based on the methodology, for example Microsoft Projects, in which are used to calculate all completion times based on a required input. The programs are further able create a visualization the whole project in which is used to ease overview and understanding as well as supporting the monitoring of the project as a whole. But the methodology can easily be applied manually to smaller problems in which will be the case here. Despite that, a knowledge of the concept is important, thus the ones who manage projects have to deal with multiple challenges within planning, coordinating and monitoring all project activities in order to complete the project of interest successfully within agreed time, cost and scope as well as according to customer quality requirements.[4]
Methodology
The Critical Path Method (CPM) can be divided into the following steps:
- STEP 1: Developing the Project Network
- STEP 2: Constructing the Project Network
- STEP 3: The Computation Process of forward pass, backward pass and slack
- STEP 4: Critical Path Identification
- STEP 5: Update of project progress
The methodology will be explained step-by-step as well as with example in Chapter 3.
Step 1: Developing the Project Network
The following input requirements are needed in order to construct a network model of the project of interest: [2]
- A list of all activities required to comlete the project also known as the work breakdowm structure (WBS)
- The duration of each individual activity for completion
- The dependencies between the activities
With this information, the critical path method is able to determine the longest path of activities through the project network, defined as the critical path and the corresponding activities are defined as critical activities. Based on the fact that the entire project cannot finish until all the activities are completed, the longest path or the critical path gives also the minimum required time to complete the entire project.
Step 2: Constructing the Project Network
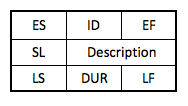
The CPM notation used for each and every activity in the project network can be seen in Figure 2. Therefore, for all activities in the network the following information is registerd and/or computed:
- ID: Identification code of individual activity
- DUR: Duration time of individual activity based on the WBS
- Early Start (ES): The earliest starting time of an individual activity
- Early Finish (EF): The earliest finishing time of an individual activity
- Late Start (LS): The latest starting time of an individual activity
- Late Finish (LF): The latest finishing time of an individual activity
- SL (Slack): The tolerance of delay of an individual activity without affecting imposed completion date
Step 3: The Computation Process
The network computation process involves drawing the project network by placing the activities that need to be completed in the right logical sequence based on their interdependencies. The methodology involves the two procedures of forward pass used to compute earliest times, ES and EF, and backward pass used to compute latest times, LS and LF. [2][9]
Forward Pass begins at the initial activity and traces each path through the network step-by-step, to the end of the last project activity/activities. An important rule of the forward pass prodeadure is that all immediate predecessors must be completed before a succeeding activity can start. That is, early start (ES) of an activity equals the largest early finish (EF) of the immediate predecessors.
For the starting activity/activities of the network, ES = 0 (or some other known value) and each path is traced forward to the finishing activity/activities by applying EF = ES + DUR to all activities in the project network. When finished, the longest path denotes the project completion time for the plan, that is, largest EF = Total Time. [9]
Backward Pass is initiated after the forward pass has been compleated and starts with the last project activity/activities without successors and the late finish (LF) is set as equal to the maximum early finish (EF) for those activities. Note that in cases where imposed project duration deadline exists, that deadline is used as late finish (LF) instead. An important rule of the backward pass is that at the latest time a succeeding activity can start is only when all immediate predecessors are completed. That is, late finish (LF) for an preceeding activity equals the smallest late start (LS) of the immediate successor activities.
With that in mind, each path is traced backward towards the inital starting activity/activities by applying LS = LF - DUR. When this has been applied to all the activities in the project network, the total slack of an activity can be determined by using SL = LS – ES or LF – EF. [9]
Step 4: Critical Path Identification
The critical path is of great importance since all critical activities must be completed as scheduled in order to meet the scheduled project completion time, that is, if an activity on the critical path is delayed, the project is delayed by the same amount of time. This is due to the fact that the activities on the critical path have a zero slack. Slack (SL) is defined as the amount of time an activity can be delayed without delaying the whole project. Therefore, project managers need pay close attention to the critical path activities in order to ensure that they are not delayed and therefore put the entire project in the risk of being late.
Step 4: Update of project pogress
FAFAFAF
CPM Example
In order to gain understanding of the critical path method, the following example is provided.
Constructing the CPM Project Network
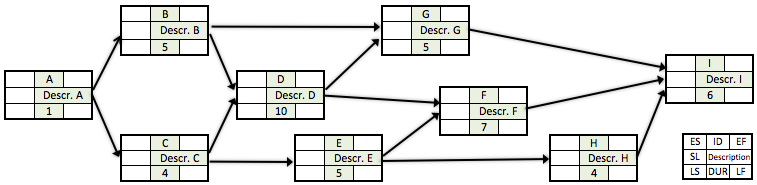
Table 1 provides information on 9 activities required to complete a project of intrest as well as their dependencies and duration times. Based on those information, the project’s needs can be translated into a network diagram in which the CPM can be utilized. The diagram graphically shows the project flow and precedence relationships among all project activities and gives the project manager a visual represensation of the entire project.
| Activity | Duration [Weeks] | Predecessor | Decription |
|---|---|---|---|
| |
|
|
Constructing a base |
| |
|
|
Build and construct wall structure |
| |
|
|
Create bearings for the roof |
| |
|
|
Raise the roof |
| |
|
|
Isolate and close the walls |
| |
|
|
Insert windows and doors |
| |
|
|
Prepare floors and lay parquet |
| |
|
|
Prepare the outside area |
| |
|
|
Paint walls and interior |
A network model of the project of intrest represented in Table 1 can be seen in Figure 3 where all project activities have been placed in the right logical sequence based on their interdependencies, using the project activity notation presented in Figure 2. This is the inital starting point of the critical path method.
The CPM Computation Process
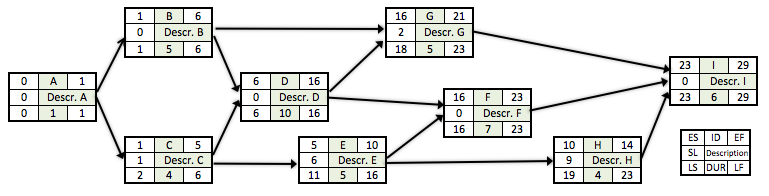
Following the CPM methodology presented earlier, the first step is to perform the forward pass. Activity A has no predecessors and therefore we assume that the activity can start as soon as the project can start, at time 0. The earliest finish (EF) date for activty A can now be computed as 0 + 1 = 1. Activities B and C have activity A as their immediate predecessor with early start (ES) as 1 and early finish (EF) as 1 + 5 = 6 and 1 + 5 = 5. Activity D is a merge activity since it is preceded by both B and C. The early start (ES) of a merge activity depends on the largest early finish (EF) of all activities that merge to it, since the activity cannot start until both the predecessing activities have finished. Therefore, early start of activity D is max(6(EF-B),5(EF-C)) = 6. By continuing the forward pass, the early start (ES) and early finish (EF) for all activities can be computed as shown in Figure 4. When the forward pass has been completed, it can be seen that the early finish for activity I or the project in total is 29 weeks.
The second step in the CPM methodology is the backward pass starting with the last project activity, which is I. The late finish (LF) of the finishing node I is set equal to its early finish (EF) of 29 weeks and late start (LS) can be computed as 29 - 6 = 23. The finishing node I is an immediate successor of activities G, F and H, hence the latest finishing (LF) time for all the three activities is set to 23 and their late starts (LS) are computed as 23 - 5 = 18, 23 - 7 = 16 and 23 - 4 = 19. Activity E is a burst activity since it is a immediate predecessor for both activities F and H. Hence, the late finish (LF) for activity E is controlled by the smallest late starts (LS) of the two successing activities since activity E cannot finish later than the latest start of an immediate successor. Therefore, late finish (LF) of activity E is min(16(LS-F),19(LS-H)) = 16. If the backward pass is continued until the starting node, the late start (LS) and late finish (LF) for all activities can be computed as shown in Figure 4.
Slack Computation and Critical Path Identification
After the completion of forward and backward passes, it is possible to determine which activities can be delayed by calculating the slack for individual activities in the project network. The slack for activity A is 0 since there is no difference between ES/EF and LS/LF. On the other hand, the slack for activity C is 2 - 1 = 6 - 5 = 1. The slack for individual activities can be computed as shown in Figure 3. After the slack computation, the critical path can easiliy be identified as the longest path through the network with critical activities consisting of zero slack. The critical path in this example is: A – B – D – F – I. . That is, if an activity on the path is delayed, the project is delayed by the same amount of time
Consdideration of Time-Cost trade-offs
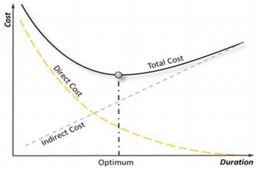
Based on acquired information from the critical path method (CPM), the next questions could be if it is possible to shorten the project in order to finish within certain deadline and what is the least expensive way to do it. Project crashing is a procedure to identify the cost of reducing project duration so that comparisons can be made with the benefits of getting the project completed earlier. It requires information of the total project cost, which includes both direct and indirect costs. Shortening the project duration will normally increase the direct costs, which can be assigned directly to project activities and commonly represents labour, materials and etc. Meanwhile, a reduction in project duration indicates a reduction in indirect costs, necessary costs for doing work which continues for the life of the project and is not related to individual project activities. Therefore, the time-cost trade-off analysis can help to identify the optimum cost-time point between increasing cost of individual activities and decreasing overall project costs. The outcome of such analysis results in a time-cost trade-off curve as shown in Figure 5. [13][14]
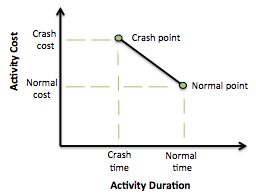
Normal time for an activity represents estimated activity duration under normal conditions retrieved from the CPM and normal cost refers to the corresponding cost of that activity, which implies minimum direct cost. Crashing refers to speeding up the duration of an activity and the crash time is the shortest possible time an activity can be completed in. The direct cost for completing an activity in its crash time is called crash cost. The cost-time relationship is assumed to be linear as shown in Figure 6 and for each activity a crash cost per period can be derived as:
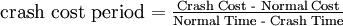
That is, the slope gives information about the cost per unit of time for shortening an individual activity and therefore allows comparison of which critical activities to shorten in order to minimize the total direct cost. [2][9][13]
After having utilized the CPM, the procedure for project crashing involves the following steps: [9][13]
- Compute the crash cost per period for all activities in the project network
- Find critical path(s) and critical activities in the project network
- In the case of only one critical path, identify a critical activity with the smallest crash cost per period that can still be crashed. Otherwise, identify critical activity/activities from each critical path with the smallest crash cost per period, which can still be crashed.
- Reduce the duration of the critical activity/activities identified in step 3 by one time unit.
- Stop the procedure if the desired completion deadline is reached. Otherwise, reconstruct or adjust the project network based on changes made in step 4 and return to step 3. Continue until the crash point has been reach, that is, no further shortening is possible.
An example of project crashing where the procedure is utilized and explained step-by-step is available here. The procedure can be used as a continuation of the example that was provided above with the CPM methodology with relatively small changes.
Benefits of CPM
Here I am going to write about the benefits of the method!
- Benefits in planning, sceaduling and monitoring
Limitations of CPM
Here I am going to write about the limitation to the method.
- Details known with certainty - make use of PERT, these detailes are not known with certenty so with combination of those two as mentioned in the Overview chapter
References
- ↑ 1.0 1.1 1.2 Project Management Institute. (2008). A Guide to the Project Management Body of Knowledge. 4th Edition. p. 6. USA. ISBN 9781933890517
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Larson, E. W & Gray, C. F. (2014). Project Management - The Managerial Process. 6th edition, p. 161. USA: NY. ISBN 9781259010705
- ↑ Newbold, R.C. (1998). Project Management in the Fast Lane – Applying the Theory of Constraint. USA: FL. ISBN 9781498738064
- ↑ 4.0 4.1 4.2 Larsen, J. & Clausen, J., (2009). Course material in Networks and Integer Programming Supplementary at DTU - Notes to Networks and Integer Programming. Retrieved from campusnet.dtu.dk
- ↑ Project Management Institute. (2010). The Value of Project Management. Available Online Version
- ↑ 6.0 6.1 Wikipedia. The Project management Triangle. Retrieved 10.08.2016
- ↑ International Organization for Standardization (2012) ISO 21500 – Guidance on Project Management.
- ↑ Mind Tools. The Iron Triangle of Project Management. Retrieved 10.08.2016 from MindTools online page
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 Chapter on Deterministic Decision Models. (n.d.). Course material in Network Optimization at DTU autumn 2015. Project Scheduling: PERT/CPM. Available online
- ↑ Anderson, E. B., & Hales, R. S., (1986). Critical Path Method Applied to Project Planning: FEES. United States Department of Agriculture. USA. Available Online
- ↑ Stelth, P. (2009). Project’s Analysis through CPM (Critical Path Method). Isles International University. Available Online
- ↑ Hegazy, T. (1999). Optimization of construction time – Cost trade-off analysis using genetic algorithms. Figure of Time-Cost Trade-Offs Retrieved 09. September 2016. Available online
- ↑ 13.0 13.1 13.2 Chapter on Project Time-Cost Trade-Offs. (n.d.). Retrieved 15.08.2016. Available online
- ↑ CPM Tutor. (2010). Time-Cost Trade-Off . Retrieved 15.08.2016 Available online
Annotated Bibliography
I know this is left - did not manage to do it :)