Application of Dependency Structure Matrix in Time Scheduling
(→DSM in a time scheduling perspective) |
|||
| Line 8: | Line 8: | ||
==How to Read the Matrix== | ==How to Read the Matrix== | ||
| + | |||
| + | [[File:Placeholder.jpg|300px|thumb|right|Figure 1: Example figure text]] | ||
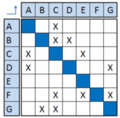
The matrix consists of all the project tasks listed as both rows and columns. This means that the matrix is an nxn square matrix where n is the number of activities. The diagonal of the matrix lists the elements themselves and the off-diagonal elements lists the dependencies by either and ‘X’ mark or a ‘0’/left out. It is crucial for the use of the activity based matrix that all the tasks are listed in progressing order from the first in the upper left to the last in the bottom right. | The matrix consists of all the project tasks listed as both rows and columns. This means that the matrix is an nxn square matrix where n is the number of activities. The diagonal of the matrix lists the elements themselves and the off-diagonal elements lists the dependencies by either and ‘X’ mark or a ‘0’/left out. It is crucial for the use of the activity based matrix that all the tasks are listed in progressing order from the first in the upper left to the last in the bottom right. | ||
Revision as of 08:46, 12 June 2017
In planning management with regards to time scheduling there are several ways to get an overview of the number of activities in a timeline like the Gantt plot or using the Critical Path Method (CPM) to estimate the time used and needed for activities dependent on each other. But CPM is limited in the way that it only looks at sequential activities though it is possible for a design case to have both dependent activities as well as interdependent activities. This means that the information flow is not necessarily linear but can be cyclic giving rise to situations where some activity is initiated but still needs information from a later activity. The structure of these activities through time can be sorted in a Dependency Structure Matrix (DSM) which marks all the interdependencies in a square matrix. The matrix can both be used for visualization and optimization of information flows. This article will discuss the application of DSM for use in a time scheduling situation of project management. Here some of the common ways to rearrange or change the matrix to reduce loops of information flow or to let non-dependent activities run in parallel will be discussed.
Contents |
Background
For planning in construction of buildings a simple Gantt chart may be of use to schedule the work flow of different tasks. Otherwise a CPM analysis (Critical Path Method) or PERT model () can be used to sequence the different tasks such that the total cost and work time is optimized. But these models are limited to progressive flows of work meaning that the completion of one task leads to the possible start of another activity. But when designing the building a lot of iterative procedures are performed which cannot be modelled by CPM for instance. These iterative procedures imply that some tasks are not just dependent on each other but also interdependent. These cycles of iteration can lead to over-designing of the project which entails waste of time and extra costs. Donald V. Steward proposed a method in 1981 using a Design Structure Matrix to optimize the information flow for the design scenario. It was later called Dependency Structure Matrix as it went from being useful mostly for the information flow during the design phase to also being applicable for other cases, not only scheduling. Several types of DSM can be used for different purposes. There are ………… but this article will focus on the use of activity based DSM.
How to Read the Matrix
The matrix consists of all the project tasks listed as both rows and columns. This means that the matrix is an nxn square matrix where n is the number of activities. The diagonal of the matrix lists the elements themselves and the off-diagonal elements lists the dependencies by either and ‘X’ mark or a ‘0’/left out. It is crucial for the use of the activity based matrix that all the tasks are listed in progressing order from the first in the upper left to the last in the bottom right. There are two ways of reading the matrix, the IR/FAD and IC/FBD convention. The first one is the one typically used for scheduling activities in construction. This states that the rows list all the requirements or inputs that a certain task needs to have to begin. The columns on the other hand list all the outputs from the activity. This means that all the interdependencies can be stated for the whole project in a single matrix. In the other convention, the way of looking at the rows and column is reversed effectively meaning that the matrix is transposed. Thus, all the observations in the following are based on the IR/FAD convention but can easily be converted to the IC/FBD convention by reversing the rows and columns. Especially the elements in the upper triangle of the matrix are important. In the IC/FBD convention these elements are therefore in the bottom triangle.
Using the Matrix/Matrix Operations
The position of the ‘X’ marks in the matrix tells about the type of processes in the project. No mark results in no correlation meaning that the processes are independent or parallel. A single mark results in a correlation giving the typical dependent or sequential process. There is lastly the type of interdependent or coupled tasks which can also be seen in loops. These can be seen by cross-diagonal markings which is the coupled tasks and markings that fit within an imaginary box with center at the diagonal are the circular tasks or loops. It is especially the interdependent or circular processes that are of interest as these define the large amount of rework or iteration needed for the full completion of the project. In the standard notation all the marks below the triangle define the linear dependencies meaning that if the matrix was a lower triangle matrix all the tasks could run in the defined order without iterations. But any marks in the upper triangle part of the matrix show the feedback from a later process to a previous one thus giving rise to iterations of work. The whole point of using DSM is to reduce the amount of rework or eliminating it by making good approximations which effectively cancels the need for the feedback information. The way all the processes are ordered is not necessarily the best solution for the sequence. By making different operations on the matrix this can be optimized. The methods for optimization are called sequencing or partitioning and tearing.
Shearing
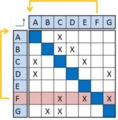
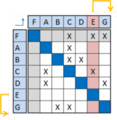
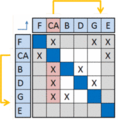
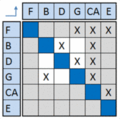
Sequencing alters the order in which the tasks are completed. This can be done by several methods like Path Searching, Powers of the Adjacency Matrix Method, the Reachability Matrix Method among others. An overview of how the more simple Path searching method works is illustrated in the following.[1] It is worth noting that the IC/FBD convention is used in the figures.
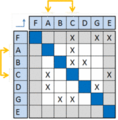
After applied sequencing the matrix is optimized with respect to the order of the independent tasks and the interdependent tasks are clustered so that less time is used before an iteration is completed. Obviously this is the best sequence of the tasks if they should run with iterations but this is a costly affair. Thus the links in the circular tasks are attempted to be severed. The process of tearing is discussed in the following.
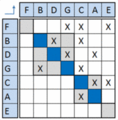
Tearing
The circular path of some activities is severed by using assumptions for the feedback information. This means that a mark in the upper triangle can be discarded and the process of sequencing can be reused to optimize the blocks of interdependent tasks. Though several feedback marks can be present in the same block. It is not wanted to tear all the markings in upper triangle. If the optimal solution is sought maybe only one tear is needed and resequencing can solve the interdependencies for the block. The way of choosing the most critical tasks, where assumptions can be made, is a very important step and no general solution is given. It all depends on the type of project and the given activities. Here the use of a numerical DSM can come in handy.
Establishing the Matrix
Performing operations on the matrix is per se the easiest or most reliable part of the process. Though to even get to having a DSM one needs to extract information about the project tasks and information flows from the people actually working with the different activities of the project. This is not so easily accomplished.[2] Through study and interviews with the managers and the experts of the project all the sub-systems and how they interact is to be defined such that the elements of the DSM can be established.[1] But it is crucial that all the information links between tasks are mentioned before performing operations on the matrix. The bias of missing marks can lead to severe problems with reworking. This means that gathering information to establish the DSM has to be accurate for it to work. Interviews seem to be a better way of extracting accurate information for a task than other methods.[1] In relation to this it seems that the appropriate people at each task are better at knowing what information they need and where to get it rather than what happens with the information that they produce. This is important to keep in mind when interviewing the different people involved.
A guide to build a credible DSM is seen in the following [1]:
- Define the system and its scope
- Here the boundary of the system is established. Different scopes lead to different DSMs so the definition is important for the accuracy of the matrix.
- List all the system elements
- Based on the review of involved energineers or experts all the elements in the system of the project are defined. If the project process is well established it can be based on existing project plans as well.
- Study the information flow between system elements
- Both design documents and more importantly interviewing the people involved can lead to knowledge of how information is transferred between project tasks. Here it is worth noting that engineers might suggest that two tasks are related when in fact they are related indirectly. The designer of the DSM needs to be aware that only directly related tasks should be marked in the DSM.
- Complete the matrix to represent the information flow
- From the information either a binary or numerical DSM can be build. The binary matrix is best for preliminary analysis but a numerical DSM will be better during the tearing phase.
- Give the matrix to the engineers and managers to comment on and use
- Giving the matrix to engineers may make them see the project in a bigger picture as well as perform more appropriate communication with the other actors. The comments may further refine the structure of the matrix.
DSM in a time scheduling perspective
DSM is mostly used for sequencing activities in a design phase but has a lot of potential for application in time scheduling. Finding the normal project duration corresponds to all activities being started after another. But in reality many of the activities have a start-up period gathering information from the relevant tasks prior to the ongoing. This results in extended durations when using a no-overlap approach of activities. But the information is rarely released all at the end of the activity which means that a natural overlap will be possible such that task durations can be shortened. Also, the successor activity can start before having all information. It is such that this process of information exchange can be modeled by use of DSM. In a DSM, where the diagonal cells represent the work done and the off-diagonal cells represent the communication time, formulae for the normal project duration can be established. Furthermore Maheswari and Varghese have presented a method for calculating the natural overlap project time when also using matrices that represent the time of earliest release of information as well as latest need for the information in the successor task.[3] The only problem with this found method is that it is assumed that tasks are fully sequenced meaning that no marks are left in the upper triangle. But if tasks where to be interdependent as well, the natural overlap time would be much more difficult to calculate as several iteration cycles needed to be included. This means that the state of the art of this method is not really useful as of now. It has a lot of potential but researchers are in progress of evolving the method of using DSM in time scheduling.
Advantages of the Method
The matrix will even for large project scopes give a visual representation of the interdependency of the processes. This will allow engineers and managers to better understand the big picture of the project.
The matrix is vital in representing information flow as neither the Gantt chart nor CPM is capable of doing so.
Disadvantages of the Method
The matrix requires a lot of accuracy with regards to establishing the matrix. Leaving a process link out of the matrix or introducing a lot of weak links which are not really necessary can lead to non-optimal solutions after matrix analysis.
The matrix does not take into account the durations and resources needed for every task. So it is not yet a complete programming method in and of itself.
The state of the art when using the matrix in time scheduling is not optimal. It has a lot of potential but not many has made reasearch in this regard so it is not that useful as of now.
Annotated Bibliography
- Articlename[4]
- text
- AUSTIN, S.A., 2000. Analytical Design Planning Technique (ADePT): a dependency structure matrix tool to schedule the building design process. Construction Management and Economics, 18(2), pp. 173-182.[5]
- text
- Charlesraj, V P C, Maheswari, J U, Kalidindi, S N and Varghese, K (2004) Knowledge management for planning construction projects using dependency structure matrix. In: Khosrowshahi, F (Ed.), 20th Annual ARCOM Conference, 1-3 September 2004, Heriot Watt University. Association of Researchers in Construction Management, Vol. 2, 831-8.[6]
- text
- Flanagan, T., Scott, T.J. and Dojen, R., "Leveraging Dependency Structure Matrix (DSM) and System Dynamics in Combination to Reduce Project Rework", 26th International Conference of The System Dynamics Society 2008, 20-24 July 2008, Athens, Greece, Paper No. 369.[7]
- text
- Maheswari, J U, Varghese, K (2005) A Structured Approach to Form Dependency Structure Matrix for Construction Projects, ISARC 2005 - September 11-14, Ferrara (Italy).[2]
- text
- Jonsson, M T (2015) Power Plant Maintenance Scheduling using Dependency Structure Matrix and Evolutionary Optimization, Proceedings of the World Congress on Engineering and Computer Science Vol II, October 21-23, San Francisco, USA.[8]
- text
- https://ocw.mit.edu/courses/engineering-systems-division/esd-36-system-project-management-fall-2012/lecture-notes/MITESD_36F12_Lec04.pdf[9]
- text
- Maheswari, J U , Varghese, K (2005) Project Scheduling using Dependency Structure Matrix, International Journal of Project Management, Volume 23, Issue 3, April, Pages 223-230.[3]
- text
- Winch, Graham M, Wiley-Blackwell, 2010, Managing Construction Projects, 2nd edition, pp. 300.[10]
- text
References
- ↑ 1.0 1.1 1.2 1.3 1.4 http://www.dsmweb.org/en/understand-dsm/technical-dsm-tutorial.html
- ↑ 2.0 2.1 Maheswari, J U, Varghese, K (2005) A Structured Approach to Form Dependency Structure Matrix for Construction Projects ISARC 2005 - September 11-14, Ferrara (Italy).
- ↑ 3.0 3.1 Maheswari, J U , Varghese, K (2005) Project Scheduling using Dependency Structure Matrix, International Journal of Project Management, Volume 23, Issue 3, April, Pages 223-230.
- ↑ 4.0 4.1 name
- ↑ AUSTIN, S.A., 2000. Analytical Design Planning Technique (ADePT): a dependency structure matrix tool to schedule the building design process. Construction Management and Economics, 18(2), pp. 173-182.
- ↑ Charlesraj, V P C, Maheswari, J U, Kalidindi, S N and Varghese, K (2004) Knowledge management for planning construction projects using dependency structure matrix. In: Khosrowshahi, F (Ed.), 20th Annual ARCOM Conference, 1-3 September 2004, Heriot Watt University. Association of Researchers in Construction Management, Vol. 2, 831-8.
- ↑ Flanagan, T., Scott, T.J. and Dojen, R., "Leveraging Dependency Structure Matrix (DSM) and System Dynamics in Combination to Reduce Project Rework", 26th International Conference of The System Dynamics Society 2008, 20-24 July 2008, Athens, Greece, Paper No. 369.
- ↑ Jonsson, M T (2015) Power Plant Maintenance Scheduling using Dependency Structure Matrix and Evolutionary Optimization, Proceedings of the World Congress on Engineering and Computer Science Vol II, October 21-23, San Francisco, USA.
- ↑ https://ocw.mit.edu/courses/engineering-systems-division/esd-36-system-project-management-fall-2012/lecture-notes/MITESD_36F12_Lec04.pdf
- ↑ Winch, Graham M, Wiley-Blackwell, 2010, Managing Construction Projects, 2nd edition, pp. 300.