Risk Assessment in Construction Industry

Revision as of 10:18, 22 June 2017

Risk management is probably the most complicated aspect within the management of a project. Especially in construction projects, the risks can be highly numerous and mostly unpredictable^[1]. A risk in a project can be defined as “an uncertain event or condition that, if it occurs, has a positive or negative effect on at least one project objective”^[2]. The larger the project the higher the risks to which the project is exposed. In fact, construction projects face a very uncertain environment consisting of planning, design and construction. Each phase requires the collaboration between multiple groups, e.g. owner, consultants, contractors, suppliers, and parties involved for the resources, finance, politics and regulations^[3][4].

Furthermore, the time to conclude a project can be very extensive and, with time, changes occur in people’s meanings, technologies, etc. Risk management should, therefore, be a daily, on-going process throughout the whole life-cycle of a project through continuous monitoring and controlling of the risks.

In order to successfully mitigate the risks during the project, the manager needs to make decisions. These decisions require a detailed assessment of the identified risks. Therefore, Risk management and decision-making tools go hand-in-hand throughout the whole project.

In this article different methodology of risk assessment and decision-making will be described according to recent literature regarding risk assessment in construction.

Background

Risk management is a daily, on-going process all throughout a project’s life-cycle. It consists in identifying, assessing, analyzing and prioritizing risks in order to apply coordinated and economical resources to minimize or maximize the risks^[5], whether they are considered as threats or opportunities respectively. Despite the skepticism around the Risk management, the latter has been proven to have much potential in managing construction projects. Together with the Risk Identification Process, Risk assessment is probably the most important step to secure a successful project, as Winch^[6] says “If the project is the process of reduction of uncertainty through time, then managing risk and uncertainty is at the heart of the management of projects”.

In the years, multiple methodologies from different authors have been used to try and make the Risk management efficient. According to Taroun et al.^[7], no theory or tool has been proven to be satisfactory in the assessment of risks. However, within construction projects, the risks are rarely in the category of unknown-unknowns^[6], which is the most complicated category to manage. It is, therefore, possible to use tools and theory to maximize the efficiency of the management of the other categories of risks: known-knowns, known-unknowns, unknown-knowns.

Risk management is the base for the decision-makers to elicit conclusions for their decisions. In such an environment, where multiple parties work together, the decision-making process is very demanding for appropriate tools to assess the risks and support the decisions. The process requires to consider multiple cases, therefore it is necessary to do a multi-criteria decision-making analysis. Over the years multiple methods have arisen for this analysis, each for different cases within a construction project. Examples of cases where a multi-criteria decision-making analysis is well suited are, according to Agnieszka and Mariusz^[8]: the variant of a project investment, contractor, location, technology of production of particular structure elements in a building, choice of a tender strategy, evaluation of tenders, specifying utility state of a building, estimation of construction costs, evaluation of accident situation in the construction industry, etc. The most commonly used methods in construction are: computer simulations, based on the probability theory, the analytical hierarchy process (AHP), the analytical network process (ANP) and the fuzzy set theory.

Statistical Approach

Probability Theory

The most useful tool behind quantitative risk assessment is the analysis of probability of occurrence of uncertain events. This analysis is based on the probability theory. There are three different schools of thought behind the definition of probability: frequentistic, classical and Bayesian.

The frequentistic definition of probability is the typical interpretation of probability for experimentalists: probability is the relative frequency of occurrence of an event over a total number n of trials in an experiment.

According to the classical definition, the probability of occurrence of an event A is given by the ratio of the number of equally likely ways by which an experiment may lead to A, and the total number of equally likely ways in the experiment.

Whereas, the first two definitions are mostly applicable to identical cases, the Bayesian definition is formulated as a degree of belief that the event A will occur^[9]. In construction, this definition is more adaptive to the risks involved in a project, as no identical cases exist. Risks are indeed unpredictable and it is mostly up to the decision-maker to define the probability of occurrence of the events. This means that there is not an absolute value of probability, but it changes according to who is doing the analysis, and is therefore subjective. However, the assigned probability may be concluded by the decision-maker's experience, expertise and preferences^[9].

Independently from which school of thought the probability is calculated, the probability theory follows three axioms. To understand them completely, the following definitions are given:

- The sample space is the collection of all possible outcomes;

- Mutually exclusive events are events that each excludes or precludes the others.

The first axiom states that the probability of occurrence of an event may be between the range of 0 and 1. The second axiom says that the probability of the sample space must be 1. And, finally, the third axiom states that given a sequence of mutually exclusive events, the probability of occurrence of all the events is equal to the sum of probability of occurrence of each event. For a better understanding of these axioms and definitions, the reader is referred to Faber^[9].

Computer Simulations

Based on the probability theory, methods and tools to calculate the probabilities are developed. Computational simulations are some of the most powerful tools to analyze the probability of failure of structures.

In modern management culture, the judgment of a project manager over a risk is not readily accepted, unless it is backed by a quantification of the risk through a Monte Carlo simulation or such. However, even the result of a Monte Carlo simulation is often based on subjective probabilities, and has therefore no more empirical status than the manager’s judgement^[7]. The Monte Carlo method is the origin for all the other computer techniques, which have proven to be valuable especially in those cases where the representation of the limit state function is associated with difficulties^[9]. The general idea of these techniques is to calculate the probability of failure through numerous simulations generated by a computer. The probability of failure, PF, is then simply calculated as the number of times the system fails, nF, over the total number of simulations, N. For N -> ∞ the estimation becomes exact^[9].

The main limitation for a Monte Carlo simulation is the accuracy needed for the input variables. During the simulation, range values of variables and correlation patterns are defined. If these parameters are not well analysed, the outputs will be of doubtful interest^[10].

For a more exhaustive explanation of the Monte Carlo method, please refer to Monte Carlo Simulation of Risk.

Analytical Hierarchy Process (AHP)

The risks in a construction project are numerous and need to be prioritized so that it is possible to mitigate the ones that may have the highest impacts. Prioritizing requires an analysis of assessment and comparison^[11]. The analytical hierarchy process is one of the most common tools utilized in construction to do pairwise comparisons. This process is based on a compensatory approach, where the decision-maker deals with trade-offs involved with their decisions^[12].

The process of the AHP is generally the same. The first step is to make a hierarchy of sub-problems of the main decision problem, from general to detailed levels. This step is very important as it gives the team a deeper “understanding of the problem, of its context, and of each other’s thoughts and feelings about both”^[12]. To each sub-problem is given a priority number, keeping the focus on the main problem. After the decomposition of the problem, it is possible to give comparative judgements. The concept is to construct pairwise comparisons of elements on the same level with regard to a shared criterion in the level above. For every pair a ratio of the priorities is set into a matrix, and thereafter it is possible to calculate a local scale of weights for each criterion.

Hierarchy for choosing a college^[13]

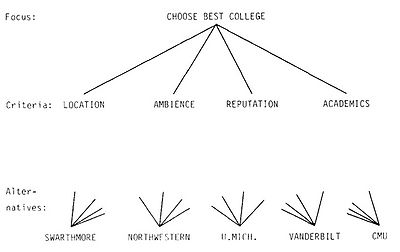
Given the comparisons, the last step is to synthesize the priorities. This process starts from the second level down and takes the local weights to derive a global and final scale, which, at the end, will give the best solution between the alternative outcomes. To get a better idea and understanding, it's suggested to have a look at a simple example of this process given by Saaty^[13] in the selection of the best college for a student, or, similarly, at this video [1], which explains how to use the AHP in the selection of a smartphone.

A general use of this method in construction is for cost, benefit and total evaluations, contractor and design assembly selections. Furthermore, it has been claimed that the use of AHP with Life Cycle Assessment is a “consistent and efficient method to appraise construction proceedings in a sustainable manner”^[14].

This method is based on personal judgement and interpretations for the comparisons, and can therefore be seen as limited. However, the judgement is usually given by experts and is probably highly reliable, and if multiple experts work on the same project, a way to overcome this will be to calculate the consistency of the experts’ judgments^[15].

Analytical Network Process (ANP)

The analytical network process (ANP) is a generalization of the AHP method which enables the existence of interdependences among criteria, which is a usual case in construction projects. For example, Lu et al.^[16] use this method for an urban bridge project where multiple construction risk problems are interdependent. Also, the selection of the contractors is influenced by multiple criteria, which are dependent to one another, as discussed in^[17] and ANP is more appropriate.

Interdependencies in ANP^[17]

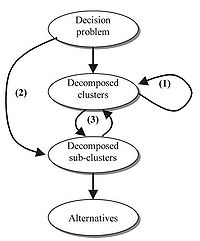
The interdependence can occur in three ways^[17]:

1) uncorrelated elements are connected;

2) uncorrelated levels are connected;

3) dependence of two levels is two-way (i.e. bi-directional).

The figure shows an example of where these interdependencies can occur.

Similarly to the AHP, a super-matrix is generated where the interdependencies are taken into account. The super-matrix adjusts the relative importance weights in individual matrices to form a new ‘overall’ matrix with the eigenvectors of the adjusted relative importance weights^[18]. According to Sarkis^[19], the ANP comprises four main steps:

1) Conducting pair-wise comparisons on the elements at the cluster and sub-cluster levels;

2) Placing the resulting relative importance weights (eigenvectors) in submatrices within the super-matrix;

3) Adjusting the values in the super-matrix so that it can achieve column stochastic;

4) Raising the super-matrix to limiting powers until the weights have converged and remain stable.

This method is a big step forward in order to assess complicated construction project risks that decision-makers have to face nowadays. Despite the dependency of the judgement matrices on subjective and/or objective ratings, this method is highly approved in the prioritizing process of risks in the construction industry^[17].

Fuzzy Sets

Basic Concepts

Degree of Belief for Management Efficiency^[20]

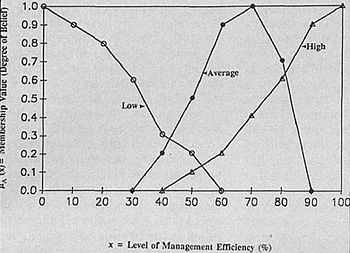
Let’s take the same example as in Kangari et al.'s paper^[20], in which the goal is to estimate the profitability [Z] of a project. According to a project manager, the set profitability is a function of three sub-sets:

1. Management efficiency [E];

2. Productivity [P] and;

3. Marketing [M].

These sets and sub-sets are considered as linguistic variables, to which a value is given – such as “low”, “average”, or “high”. The project manager provides a graph against the degree of belief (or membership value) for each value based on elements of judgement (see figure, where the sub-set [E] is graphed). The degree of belief is in the range of [0, 1], where 0 means that the element is not a member of the set, and 1 means that it is a member.

A project can be considered profitable if its marketing and efficiency, or its marketing and productivity is “medium” – profitability is described as “low”, “medium”, or “high”. In logical terms, this can be described as:

The union of two fuzzy sets is defined as the larger membership value between the two, whereas the intersection is the lower membership value. Finally, let’s assume that the project manager wants to know if a project is likely to be profitable, given that it has “Average Management Efficiency”, “Average Productivity” and “Excellent Marketing”. Solving the logical equation, the following results shown in the figure are achieved.

Estimated Profitability^[20]

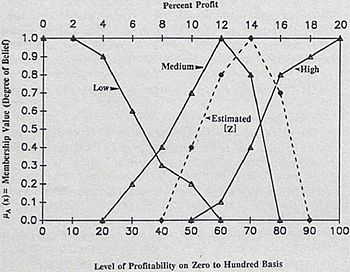
The curve of the estimated profitability [Z], is clearly between the medium and high level of profitability, and the project is, therefore, considered profitable.

Fuzzy Sets in the Construction Industry

Methods, such as the Monte Carlo simulations, are appropriate in the construction industry when the probability function can be precisely described. However, in the construction industry, this is often not the case. Fuzziness is an inherent characteristic in the management of uncertain events^[21], and fuzzy set analysis has been found to be useful in modelling the risks and uncertainties in some cases, e.g. investment appraisal, network scheduling, and project monitoring and control.

Olubukola and Sam^[22] conducted a study on the use of the fuzzy set theory in the UK. They concluded that the fuzzy set theory facilitates the decision-making process by rationalizing and enhancing the ideas and reasoning of a project manager. It has been proven that it helps meeting the time targets, estimating more accurate construction costs and achieving safety and environmental sustainability requirements. The advantages provided by the tool would, however, be null if used as stand-alone. The best use of it can be achieved by combining its logic with insights drawn by other mathematical formulations, such as the probability theory, the Monte Carlo simulations and the AHP.

It has been discovered that, for highly repetitive and small-in-scope projects, e.g. roadwork maintenance and household renovation, the fuzzy set theory is a superfluous model when considering economics of scale, time and resources^[22]. Furthermore, the tool should be implemented in the middle stages of a complex project – detail design and execution – and not in the early or later stages. In the early stages, the lack of information does not provide a robust structural framework for risk analysis, whereas in the last stages, the risks are diminished and, therefore, the tool is of low application^[23].

Annotated bibliography

(1) Michael Havbro Faber. Statistics and Probability Theory. Springer. 2012.

The probability theory for risk assessment is an enormous topic which needs to be studied in deeper terms. This book touches all the aspects of statistics and probability theory in supporting engineering decision making.

(2) Taroun, A., Yang, J.B. and Lowe, D. The Built & Human Environment Review, Volume 4, Special Issue 1. Manchester Business School. Pp. 87-97. 2011.

In the past three decades, the risk management has been given more and more space into the overall project management. In this article, it is given a literature review of different authors, from different parts of the world, that have proposed their approaches to get the best out of the risk management. However, no technique has proven to be satisfactory enough to be used as a fundament for every case.

(3) Daniel J.-E., Elena C.-L., Jorge R.-H., Juan C. C.-J. A review of application of multi-criteria decision making methods in construction. Automation in Construction 45. Pp. 151-162. 2014.

Multi-criteria decision making is another topic which requires a further look into it. This article gives an overview of where the different methods of the multi-criteria decision making can be used, based on the review of 88 research papers.

(4) R. W. Saaty. The Analytical Hierarchy Process-What it is and how it used. Mathl Modelling, Vol.9, No. 3-5, pp. 161-176. 1987.

The Analytical Hierarchy Process is a simple tool which is used in everyday situations when making decisions that require trade-offs. In our minds we give different priorities to different criteria and elicit the best solution for us. In more complex situations, it is useful to follow a pre-defined scheme and rules. In this volume, the steps and process are well described in practical cases, as well as through mathematical fundamentals. 

(5) Eddie W. L. Cheng and Heng Li. Construction Management and Economics, 22, 1021–1032. Department of Building Real Estate, the Hong Kong Polytechnic University. 2004.

The Analytical Network Process is a more effective and extensive method of the AHP. In this paper the two methods are compared through an example of contractor selection, and the authors give a deep insight of the process. It is highly suggested to read it for a better understanding of the potential and use of this tool.

(6) Olubukola T., Sam W. Perceptions of Fuzzy Set Theory in Construction Risk Analaysis. In: Smith, S.D (Ed) Procs 28th Annual ARCOM Conference, 3-5 September 2012, Edinburgh, UK, Association of Researchers in Construction Management, 1197-1207. School of Engineering and the Built Environment, Edinburgh, UK. 2012.

The paper is a research consisting in both interviewing and analyzing a set of questions sent to 77 experts in the construction industry in UK, who are familiar with the fuzzy set theory. Olubukola and Sam provide a well-done analysis on the advantages and disadvantages of the tool, specifying where it is more appropriate to use and its limitations.

References

1. ↑ Nerija B, Audrius B. Chapter 19: Risk management in construction projects. In: Risk Management – Current Issues and Challenges. Vilnius Gediminas Technical University, Vilnius, Lithuania. 2012.
2. ↑ Project Management Institute. Guide to the project management body of knowledge (PMBOK® Guide). 4th ed. Newtown Square: Project Management Institute; 2008.
3. ↑ Dey PK. Issues and challenges of managing projects in India: A case study. In: Budhwar PS, Varma A, editors. Doing business in India: Building research-based practice. New York: Routledge; 2011.
4. ↑ Dey PK, Ogunlana SO. Risk based decision support system for effective implementation of projects. Int J Risk Assess Manage; 3(2/3/4): 189–204. 2002
5. ↑ Hubbard D. The Failure of Risk Management: Why It's Broken and How to Fix It. John Wiley & Sons. p. 46. 2009.
6. ↑ ^{6.0 6.1} Winch G. Managing Construction Projects. An Information Processing Approach. Second Edition, Wiley-Blackwell, United Kingdom. 2010.
7. ↑ ^{7.0 7.1} Taroun, A., Yang, J.B. and Lowe, D. The Built & Human Environment Review, Volume 4, Special Issue 1. Manchester Business School. Pp. 87-97. 2011.
8. ↑ Agnieszka D. and Mariusz R. Risk Analysis in Construction Project - Chosen Methods. Procedia Engineering 122:258-265. 2015.
9. ↑ ^{9.0 9.1 9.2 9.3 9.4} Michael Havbro Faber. Statistics and Probability Theory. Springer. 2012.
10. ↑ Shim M. Project Risk Management and the application of Monte Carlo Simulation. Quantmleap.com. 2010.
11. ↑ Martin Schieg. Risk management in construction projects. Journal of Business Economics and Management, 7:2, 77-83. Ausburg, Germany; 2006.
12. ↑ ^{12.0 12.1} M. Majumder. Impact of Urbanization on Water Shortage in Face of Climatic Aberrations. SpringerBriefs in Water Science and Technology. Chapter 2. 2015.
13. ↑ ^{13.0 13.1} R. W. Saaty. The Analytical Hierarchy Process-What it is and how it used. Mathl Modelling, Vol.9, No. 3-5, pp. 161-176. 1987.
14. ↑ Daniel J.-E et al. A review of application of multi-criteria decision making methods in construction. Automation in Construction. Pp. 151-162. 2014.
15. ↑ Mohammad A. Mustafa. Transactions on Engineering Management, vol. 38, No. 1. Project Risk Assessment Using the Analytical Hierarchy Process. 1991.
16. ↑ Shih-Tong Lu, Cheng-Wei Lin, Ping-Hui Ko, Application of analytic network process (ANP) in assessing construction risk of urban bridge project, Second International Conference on Innovative Computing, Information and Control, pp. 169–172. 2007.
17. ↑ ^{17.0 17.1 17.2 17.3} Eddie W. L. Cheng and Heng Li. Construction Management and Economics, 22, 1021–1032. Department of Building Real Estate, the Hong Kong Polytechnic University. 2004.
18. ↑ Meade, L. and Sarkis, J. Strategic analysis of logistics and supply chain management systems using the analytic network process. Transportation Research Part E: Logistics and Transportation Review, 34(3), 201–15. 1998.
19. ↑ Sarkis, J. A methodological framework for evaluating environmentally conscious manufacturing programs. Computers & Industrial Engineering, 36, 793–810. 1999.
20. ↑ ^{20.0 20.1 20.2} Kangari, R. and Boyer, L. T. Basic concepts of the theory of fuzzy sets. Project Management Journal, 20(1), 44–46. 1989.
21. ↑ Ayyub, B. Elicitation of Expert Opinions for Uncertainty and Risks. Florida: CRCPress. 2001.
22. ↑ ^{22.0 22.1} Olubukola T., Sam W. Perceptions of Fuzzy Set Theory in Construction Risk Analaysis. In: Smith, S.D (Ed) Procs 28th Annual ARCOM Conference, 3-5 September 2012, Edinburgh, UK, Association of Researchers in Construction Management, 1197-1207. School of Engineering and the Built Environment, Edinburgh, UK. 2012.
23. ↑ Ayyub, B. Risk Analysis in Engineering and Economics. Boca Raton: Chapman & Hall. 2003.