Programming a project with the CPM
(→Application) |
(→Abstract) |
||
| Line 2: | Line 2: | ||
==Abstract== | ==Abstract== | ||
The Critical Path Method (CPM) was developed in late 1950s and became a very popular tool for Schedule Development. The method, which is broadly used by project managers, is a graphical technique which is known with the generic term Network Modeling. | The Critical Path Method (CPM) was developed in late 1950s and became a very popular tool for Schedule Development. The method, which is broadly used by project managers, is a graphical technique which is known with the generic term Network Modeling. | ||
| − | The [[Wikipedia:Critical Path Method|Critical Path Method]] (CPM) is a step-by-step project management technique for process planning that defines critical and non-critical tasks with the goal of preventing time-frame problems and process bottlenecks. The CPM is ideally suited to projects consisting of numerous activities that interact in a complex manner<ref name=" | + | The [[Wikipedia:Critical Path Method|Critical Path Method]] (CPM) is a step-by-step project management technique for process planning that defines critical and non-critical tasks with the goal of preventing time-frame problems and process bottlenecks. The CPM is ideally suited to projects consisting of numerous activities that interact in a complex manner<ref name="KOSTAS" />.For both commercial and governmental organizations, the ability to manage projects effectively is a major contributor to an organization’s overall performance. Almost all project planning and scheduling tools on the market today use some type of PERT and/or CPM methodology as their primary underlying methodology. These two approaches are synonymous and are often interchanged or even collectively called PERT/CPM<ref name="kostas"> ''https://www.pmi.org/learning/library/going-beyond-critical-path-method-6297 / Project Management Institute '' </ref>. This article describes the CPM methodology and provides an example of this technique, while it analyzes how this method responds to the modern business practices.<ref name="KOSTAS" /> |
==Big Idea== | ==Big Idea== | ||
Revision as of 19:19, 13 February 2018
Contents |
Abstract
The Critical Path Method (CPM) was developed in late 1950s and became a very popular tool for Schedule Development. The method, which is broadly used by project managers, is a graphical technique which is known with the generic term Network Modeling. The Critical Path Method (CPM) is a step-by-step project management technique for process planning that defines critical and non-critical tasks with the goal of preventing time-frame problems and process bottlenecks. The CPM is ideally suited to projects consisting of numerous activities that interact in a complex manner[1].For both commercial and governmental organizations, the ability to manage projects effectively is a major contributor to an organization’s overall performance. Almost all project planning and scheduling tools on the market today use some type of PERT and/or CPM methodology as their primary underlying methodology. These two approaches are synonymous and are often interchanged or even collectively called PERT/CPM[2]. This article describes the CPM methodology and provides an example of this technique, while it analyzes how this method responds to the modern business practices.[1]
Big Idea
The Critical Path Method calculates a single, deterministic early and late start and finish date for each activity based on specified, sequencial network logic and a single duration estimate. The focus of CPM is on calculating float in order to determine which activities have the least scheduling flexibility. The CPM algorithms are often used in other types of mathematical analysis.[1]
Methodology
A specific methodology has been developed for the practical implementation of this method, generally consisting of the following steps:
1. Definition of the work or actions constituting the project as a whole. It is recommended to use the Work Breakdown Structure (WBS) to identify the activities of the project.
2. Determine the sequence with which these actions must be executed.
3. Estimate the completion time of each individual work or action.
4. Planning the network of actions while respecting the requirements of the project execution sequence.
5. Determine over the network from the beginning to the end of the project, the fastest possible start and completion of each action, based on the network and completion times.
6. Determine over the network, from the end to the beginning of the project, the later start and finish of each action, based on the fastest completion time of the project identified in the previous step.
7. Determine the time that can delay any action (time interval) based on the difference in times that were found in the previous two steps.
8. Recognize and record the critical actions that are those of where the time difference is zero (0) and cannot delay. These are the critical route.
9. Use the information from steps 5 and 6 for the basics planning of the project.
It is easy to understand that the most important steps are considered to be the assessment of the completion times of the individual actions and the determining of the critical route, that is to say, the actions to be taken that cannot delay. Thus, the CPM method can be used effectively when the time completion of each individual action of the project can be assessed with relative accuracy, and it is a deterministic variable. This happens when there is satisfactory data for the approach of the aforementioned times, i.e. statistical data from similar projects, or projects where executives, responsible for the execution may be based on technical knowledge and their experience of correctly predicting completion times of the actions. Given the completion times of the individual actions, the most important steps are the design of the network and the identification the critical route. Below, there is an application of this method that follows the methodology mentioned above.
Application
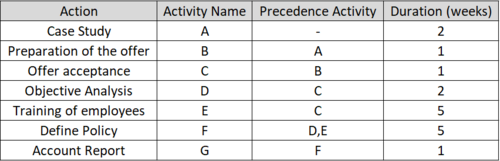
Let’s say that a consulting company carry out a project and the project team decide which individual actions are the main components of the overall project. These may be exploring customer requirements, investigate the case study, preparation of the offer, etc. These actions are shown in the first column of Table 1 below. Once established exactly the actions, they are encoded with a letter for facilitating the design of the network (2nd column of the table). Then determine the sequence, that is the order of execution shown in 3rd column of the table, where next to each action is shown which or what actions must precede. Finally, in the fourth column, there is the time required for completion of each action, estimated by the project team. So, the first thing that the project team or the person responsible for the planning must produce, is a table as Table 1.
Designing the network.
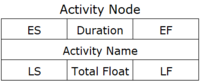
Once the above table has been determined, the project manager can proceed with the design of the network. The actions are represented as nodes while arrows from node to node show the sequence of actions. The elements that are written on a node can be seen in Picture 2.
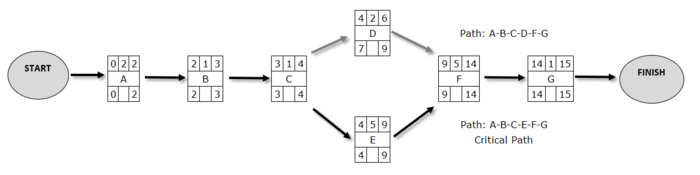
Based on the table 1, we end up with the following network of actions for the consultant company.
We notice that action C is the previous action for D and for E, while F takes place after both D and E have been completed. When planning a network of actions we need to be sure that the actions are depicted in the proper sequence and that we maintain the logic among them. In the case of the consultancy company we observe two routes, A-B-C-D-F-G and A-B-C-E-F-G.
Determination of "Critical Times" of Actions. Early Start Time (ES) - Early Finish Time (EF)
During the process of identifying the critical route, it is needed to calculate the critical times of the project's actions.
Earliest Start Time (ES) of the action is the earliest time at which the action may begin. This depends on when the previous or previous actions have been completed.
Early Finish Time (EF) of the action is the earliest time at which the action may have been completed, and apparently, equals the ES plus the duration of the action.
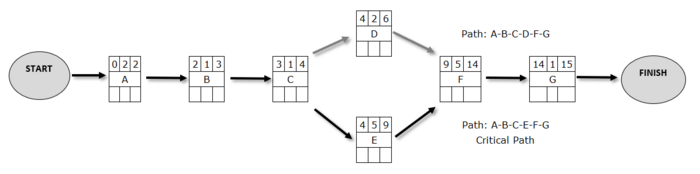
The technique to determine these times, it is considered that the work begins at time 0, so ES = 0 for action A which is the first in the sequence of actions. The shortest end time EF for Action A will obviously be ES + 2, since 2 weeks is its duration, so EF = 2. The next action is B, which of course can not begin before Action A has been completed. Therefore, the ES for action B will be identified with EF of the previous action and ES = 2 for action B. As far as it is known that the duration of action B is 1, it is obvious that EF = ES + 1 = 2 + 1 = 3. Following this process and using the duration of actions from Table 1, the network in Picture 3 is produced.
As a consequence, it is logical that the shorter completion time of the overall project is identical to the EF of the last action. This is the expected completion time of the project. In our case, the company's project has a total project duration of 15 weeks.
Determination of "Critical Times". Late Start Time (LS) - Late Finish Time (LF)
The next step in the process is to calculate the earliest starting and finishing times of the actions.
The Late Finish Time (LF) of the action is the earliest time when an action can end without extending the completion time of the entire project.
The Late Start Time (LS) of the action is the earliest time that an action can start without prolonging the completion time of the entire project and obviously equals to LF minus the duration of the action.
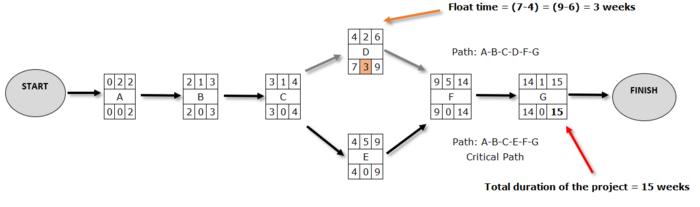
Based on the example to define the earliest times, we have to start from the end of the network towards the beginning by examining one by one the actions. As already has been proved, the shortest completion time of the project, hence the desirable time, is identified by the EF of the last action, and that is 15 weeks. So, as long as the total duration of the project does not exceed this achievable time, it is obvious that the earliest termination time LF of the action G is 15. Consequently, the action G cannot be completed after the 15th week because there will be a time extension for the company’s project. Thus, LF = 15 for action G, and obviously the LS for G will be LS = LF-1 = 15-1 = 14, i.e. the earliest start time of the action G, is the action LF, minus its duration which in our case is 1. Regarding action F, as long as the earliest time in which may be triggered by its next associated action G and it’s the 14th week (LS = 14 for G), cannot end later than the 14th week without extending the whole project time. Accordingly, the earliest termination time for the action F is LF = 14 and apparently the earliest start time will be the LF of the action minus its duration. Therefore, LS = LF-5 = 14-5 = 9 for action F. Following this procedure and using the duration times of the actions from Table 1, the network in Picture 4 is produced.
.Slack time and Critical Path
Having ES, EF, LS and LF, it is then possible to find the slack times of the actions and to identify the critical path. Slack time is the time period during which we can delay an action without affecting the completion time of the project. Obviously the slack time span of any action is the difference between LS and ES or the LF and EF of the action.
Slack time = LS-ES = LF-EF
If we calculate from Picture 4 the slack times of the actions it is observed that it is 0 for all actions except for action D for which:
Slack Time (D) = 7-4 = 9-6 = 3 weeks
It is clear, therefore, that action D can begin anytime within a period of 3 weeks from ES = 4 to LS = 7 which is the earliest time it can start, according to the network, without adversely affecting the overall duration of the project. All the other actions in the network, with slack times equal to zero, cannot delay because the total duration of the project will be affected.
Thus it is stated that:
A critical path in a network of actions is the longest in duration path from network related actions from the start until the end of a project, where any delay in these actions leads to time extension to the completion of the overall project. The critical path can also be defined as the route on the network where all its actions have zero slack time or even the path for which the pairs (ES, EF) and (LS, LF) are identified. The actions that belong to the critical path are also called critical actions. So, if any action ends up with zero slack time, this action is on the critical path. Usually, and especially in some more complex networks, there are many critical routes. Of course, the total time of the critical routes is the same and longer than the total time in any other route of the network. In the example above only action D is not a critical action, and does not belong to the critical path (since it has slack time = 3 ≠ 0). All the other actions have zero slack time (or otherwise apply to them (ES, EF)> (LS, LF)) and are in the critical path which is path A-B-C-E-F-G. In Picture 5 below it can be seen the critical path, the slack time for action D and the total duration of the project.
In the example for the consulting company's project, based on the definition that the critical path in a network of actions is the largest time path from network related actions from the start to the end of the project, it seems that with a simple overview of the network, as shown in Picture 1, without ES, EF, LS and LF and only from the durations of the actions can someone identify that A-B-C-E-F-G is the critical route. But when the action network is more complex (i.e. we have a complex project), with many nodes and more arrows, it is difficult to identify it immediately. Then the above methodology, becomes necessary to drive on critical actions, timing of other actions and eventually critical route.
Conclusions and comments for the CPM method
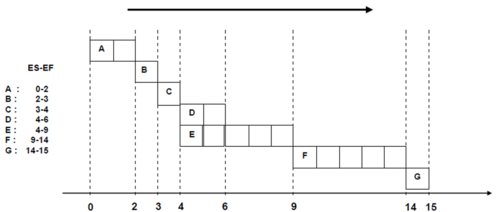
The existence of slack times in actions that do not belong to the critical route, allows for their programming in accordance with the needs and priorities of the overall project. In the example the action D was reported to have slack time 3 weeks. This allows the start of Action D at any time within the timeline from week 4 (ES = 4) to week 7 (LS = 7). This property of non-critical actions can be better observed if we use the Gantt diagram, where time is depicted in the horizontal axis. Picture 6 shows exactly this, with the non-critical action D that starts at the time that is identical to ES of (ES = 4).
This approach to programming non-critical actions is called Early Start Schedule. In this case, they are scheduled to begin as soon as possible (ES). With this approach the project and all the individual actions are completed as soon as possible.
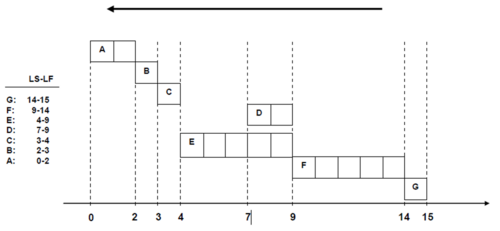
Many times, however, this is not desirable. So we can choose the very opposite approach to programming non-critical actions and have the Late Start schedule. This approach can offer better usage of the system’s resources and can be seen in Picture 7. So, it is understandable that in a complex task with several non-critical actions such programming is a very helpful tool for project managers. If we compare the two Pictures 6 and 7 from the Gantt charts we can see within which time intervals the non-critical action D can be moved. The existence of slack times for the non-critical actions facilitates their programming in a way that can we can use more efficiently the system’s resources. Indeed, the start of these non - critical actions according to their earliest start times (ES), usually implies the accumulation of large requirements and resources for inputs in some time periods. By using the available margins for any non-critical action, thus bringing the start to an appropriate time (and correspondingly end) of each such action, but always within the available margins, we achieve the most stable and uniform usage of the project’s resources.
By this way, there are several positive economic consequences for the project, as the idle time of the permanent staff and machinery decreases and we can avoid at the employment of seasonal staff, the rental of additional equipment, assigning parts of the project to subcontractors etc.
In addition to its ability to reduce the complexity of larger projects by breaking them into component tasks, the critical path method became popular because of the innovations in computer hardware and software. In the first few decades of the critical path method, the tools were bulky mainframe computers used by specialists who often required months of training. The PC revolution brought scheduling management software to the desktop, and the rise of computer networking allowed the results to be shared easily among team members.[3]
Limitations of the CPM due to the modern business practices
The CPM nowadays has the following disadvantages:
• The method assumes that the duration of the activities in the project is given (input), something that usually is not the case, as it overlooks the modern work practices such as the flexibility of work and the fact that the duration of the different activities is practically an outpout in the real business. Fuzzy or probabilistic models could enhance the method in that case.
• The usage of a software such as Microsoft Project or Primavera are recommended if the analysis process is extremely complicated.
• The method requires time in order to develop the project network and relies heavily on project managers and members involved in that stage. Poorly defined project scope and activities can result in ineffective use of CPM, which becomes difficult to manage.
• It is not easy to adjust the method when changes occur in the project plan during the project execution. In that case the we have to redraw the project and start the calculations from the beginning.
• Due to that the critical path method is an optimal planning tool, it always assumes that all resources are available for the project at all times, something that does not reflect the reality especially nowadays.
To overcome these shortcomings of the critical path, the critical chain method was developed. In the critical chain method resource constraints are also taken into consideration while developing the network diagram.[1]
References
- ↑ 1.0 1.1 1.2 1.3 A Guide to the Project Management Body of Knowledge, PMI Standards Committee, ISBN:1-880410-12-5
- ↑ https://www.pmi.org/learning/library/going-beyond-critical-path-method-6297 / Project Management Institute
- ↑ https://yourbusiness.azcentral.com/history-critical-path-method-24351.html / AZCentral.