Project viability assessment through Net Present Value (NPV)
(→Abstract) |
(→References) |
||
| (276 intermediate revisions by one user not shown) | |||
| Line 2: | Line 2: | ||
== Abstract == | == Abstract == | ||
| − | The ''' | + | The '''Net Present Value (NPV)''' is a widely used financial metric in project management. Its purpose is to evaluate the profitability of a proposed project by aggregating the streams of costs and benefits into a single value. This makes for an effective indicator of identifying profitable projects when assessing multiple projects at a time. For a given project to be considered a profitable investment, its NPV must be larger than zero<ref name="DSSA"/>. |
| − | + | ||
| + | Central to the calculation of the NPV is assigning varying weights, dependent on time, to the benefits and costs through the utilization of a so-called discount factor, which is calculated using a discount rate. The discount rate represents the rate of interest that is used to discount all future costs and benefits<ref name="DSSA"/>. By incorporating this principle, the NPV accounts for and subscribes to the paradigm of the time value of money, referring to the idea that money has a different value at different points in time<ref name ="TVM"/>. | ||
| − | NPV | + | This article explores central concepts connected to the calculation and application of NPV in the assessment of projects, programs, or portfolios. Moreover, how it relates to financial appraisals of projects and how it can support decision-makers in the process of doing so. For demonstration purposes, an example of the calculation of an emulated project's NPV will be given. Moreover, the advantages and disadvantages of using NPV as an indicator of project profitability will be addressed. |
== NPV Formula == | == NPV Formula == | ||
| + | |||
| + | The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments<ref name="NPV_H"/>. The formula used to calculate the net present value is presented below: | ||
| + | |||
| + | <math>NPV = \sum_{t=0}^{N}\frac{B_t-C_t}{(1+r)^t}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | * <math> N</math>: The calculation period of the project in years. | ||
| + | |||
| + | * <math> B_t</math>: The aggregated amount of benefits (both positive and negative) in year t | ||
| + | |||
| + | * <math> C_t</math>: The amount of investments costs in year t | ||
| + | |||
| + | * <math> r</math>: The discount rate | ||
| + | |||
| + | There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain euro tomorrow is less valuable than a euro today<ref name="NPV_P"/>. This is modulated by the use of the discount factor <math> (1+r)^t </math>, where a discount rate is used<ref name="DSSA"/>. Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to <math> t = 0 </math>. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, <math> N </math><ref name="NPV_P"/>. For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. | ||
| + | |||
| + | == Time value of money == | ||
| + | [[File:PVFV1.PNG|thumb|350 px|center|Figure 1: Basics of time value of money. Own creation. Inspiration drawn from<ref name="TVM2"/>.]] | ||
| + | Central to understanding the financial viability of future projects or investments is the concept of the time value of money (TVM). TVM deals with the truth that a euro today is worth more than a euro tomorrow<ref name ="TVM1" />. The promise of any future amount of money is affiliated with a certain degree of uncertainty, some promises are riskier than others. This means that it requires a larger sum of future euros than current euros to purchase the same number of services and goods today. Furthermore, it begs the question that receiving a specified amount of euros today, rather than later, gives the opportunity to invest the money in order to yield interest. Moving money through time involves interest as a medium to translate the values from one period to another<ref name ="TVM2"/>. Interest can be perceived as the price of the risk and the price of the time of the resources borrowed. The risk component is the uncertainty of whether the lender is able to recuperate the initial amount from which was borrowed. To see the concept illustrated, please refer to Figure 1. The time component is the possibility of spending resources differently. '''[[Wikipedia: Compound interest | Compound interest]]''' refers to the process of the time value of money over numerous periods influenced by interest<ref name = "TVM2" />. In simple terms, if a company were to borrow €500,000.00 for a project with an expected annual compound interest rate of 1.5%, after 1 year the payback amount would be €507,500.00, and after 10 years the amount would be €580,270.41. Therefore, the time horizon, interest rate, and the sum of the invested money are pivotal in determining the future value of an investment or project. | ||
== Discount rate == | == Discount rate == | ||
| − | = | + | [[File:Discountrateversus.png|thumb|500px|right|Figure 2: Discount factor versus discount rate. The discount factor as a function of t and the discount rate r. Own creation. Inspiration drawn from<ref name="DSSA"/>.]] |
| − | == Example == | + | The discount rate is the interest rate to convert future cash flows into an equivalent one-off upfront sum or present value <ref name="DISCOUNT"/>. As the discount rate increases, the lower the present value of a given future amount becomes. Hence the magnitude of the discount rate exerts a significant influence on the net present value. For instance, if the selected discount rate level is set too high, it may make potentially good projects, programs or portfolios seem unattractive, whereas if set too low, it might result in the opposite. To see how different discount rates modulate the discount factor, thus influencing the NPV of a given project, see Figure 2. |
| + | |||
| + | |||
| + | == Selection of discount rate == | ||
| + | The selection of an appropriate discount rate can be a very exhaustive and challenging task, as the decision is dependent on multiple factors, to name a few: | ||
| + | |||
| + | * The situational circumstances under which the investment project is taking place are characterized by fundamental uncertainty, computable risk, or certainty. The first, driving the discount rate to increase the most<ref name = "CHAPTER8"/>. Furthermore, the jurisdiction and location of the project being commenced also play a role in the choice of a discount rate<ref name ="EU"/>. | ||
| + | * The duration of the time horizon, especially in a socio-economic context, numerous countries have opted to differentiate between projects that span less than or more than 30-50 years, with the latter receiving a lower discount rate<ref name = "CHAPTER8"/>. | ||
| + | * Private versus public and government bodies. Discounting from a firm’s or individual perspective is inherently different than that of government bodies<ref name = "CHAPTER8"/>. | ||
| + | |||
| + | In relation to state-aided projects, the European Commission calculates and issues base rates each month for countries within the union. The discount rate can be found by adding a margin of a 100 basispoints to the base rate. The base rate for the first four months of 2023 is depicted in table 1. | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+ style="caption-side:bottom; color:black;"|''Table 1: Base rates from the European Commission<ref name ="EU"/>.'' | ||
| + | |colspan="29" style="text-align: center;"|Base rates as of 1.4.2023 | ||
| + | |- | ||
| + | |From | ||
| + | |To | ||
| + | |AT | ||
| + | |BE | ||
| + | |BG | ||
| + | |CY | ||
| + | |CZ | ||
| + | |DE | ||
| + | |DK | ||
| + | |EE | ||
| + | |EL | ||
| + | |ES | ||
| + | |FI | ||
| + | |FR | ||
| + | |HR | ||
| + | |HU | ||
| + | |IE | ||
| + | |IT | ||
| + | |LT | ||
| + | |LU | ||
| + | |LV | ||
| + | |MT | ||
| + | |NL | ||
| + | |PL | ||
| + | |PT | ||
| + | |RO | ||
| + | |SE | ||
| + | |SI | ||
| + | |SK | ||
| + | |UK | ||
| + | |- | ||
| + | |1.4.2023 | ||
| + | |… | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |1.51 | ||
| + | |3.06 | ||
| + | |7.43 | ||
| + | |3.06 | ||
| + | |3.54 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |15.10 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |7.62 | ||
| + | |3.06 | ||
| + | |8.31 | ||
| + | |3.21 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.52 | ||
| + | |- | ||
| + | |1.3.2023 | ||
| + | |31.3.2023 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |1.10 | ||
| + | |3.06 | ||
| + | |7.43 | ||
| + | |3.06 | ||
| + | |2.92 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |15.10 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |7.62 | ||
| + | |3.06 | ||
| + | |8.31 | ||
| + | |2.96 | ||
| + | |3.06 | ||
| + | |3.06 | ||
| + | |3.52 | ||
| + | |- | ||
| + | |1.2.2023 | ||
| + | |28.2.2023 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |0.79 | ||
| + | |2.56 | ||
| + | |7.43 | ||
| + | |2.56 | ||
| + | |2.92 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |15.10 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |7.62 | ||
| + | |2.56 | ||
| + | |8.31 | ||
| + | |2.44 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.77 | ||
| + | |- | ||
| + | |1.1.2023 | ||
| + | |31.1.2023 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |0.36 | ||
| + | |2.56 | ||
| + | |7.43 | ||
| + | |2.56 | ||
| + | |2.92 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |15.10 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |7.62 | ||
| + | |2.56 | ||
| + | |8.31 | ||
| + | |2.44 | ||
| + | |2.56 | ||
| + | |2.56 | ||
| + | |2.77 | ||
| + | |} | ||
| + | |||
| + | The weighted average cost of capital (WACC) is another way to determine and select an appropriate discount rate for firms, in the appraisal process of a proposed investment or project using the NPV. The WACC represents the risk to the future cashflows received by an organization from its operations including equity and debt. It weighs the cost of each capital source by its relevant weight by market value and adds it together to determine the total. The gist of using the WACC besides it representing a minimum rate of return that a firm must achieve is that it can be used as a proxy for a suitable discount rate <ref name = "WACC" />. The WACC is calculated as follows<ref name = "WACC" />: | ||
| + | |||
| + | <math>WACC = (\frac{E}{V}\cdot Re)+(\frac{D}{V}\cdot Rd \cdot (1-Tc)) </math> | ||
| + | |||
| + | Where | ||
| + | * <math>Re</math>: Cost of equity | ||
| + | * <math>Rd</math>: Cost of debt | ||
| + | * <math>Tc</math>: Corporate tax rate | ||
| + | * <math>D</math>: Market value of the company's debt | ||
| + | * <math>E</math>: Market value of the company's equity | ||
| + | * <math>V</math> = <math>D+E</math> | ||
| + | |||
| + | To summarize, the choice of discount rate has a tremendous impact on the appraisal outcome of investments or projects using the NPV<ref name = "DSSA" />. To a high extent, the selection of the discount rate is dependent on the context in which it is used. Therefore, one must be aware of the circumstances, the type of project, and the affiliated risk that the very project or investment comes with. In its most basic shape, the discount rate simply gives an insight into how profitable a future project or investment can be for a particular organization. | ||
| + | |||
| + | == Financial Appraisal == | ||
| + | The gist of financial appraisals is to deliver the maximum value for money of a project for the project implementor. Moreover, to determine the viability of the investment or project by assessing the future net cash flow as a result of the realization<ref name = "APM" />. The financial appraisal is a systematic process for analyzing alternative uses of limited assets and resources. It focuses on the assessment of benefits, costs, objectives, risks, funding, and executability. The financial appraisal facilities great management practices and it is vital to create transparency, and accountability, and make informed decisions. Financial appraisals are a difficult matter, yet an important tool, even an imperfect one, that makes it possible to compare options on a project, program, and portfolio level. It can be complemented by a '''[[Wikipedia: Business case | business case]]''', that takes the wider narrative into account on how that said the investment could be executed to realize the intended benefits<ref name = "APM" />. There are plenty of tools to choose from besides the NPV, the common nominator being comparability, such as the: | ||
| + | |||
| + | * '''[[Wikipedia: Internal rate of return | Internal rate of return (IRR)]]''' aims to determine the rate i, balancing the cost and benefit streams, simply put the rate i that equals NPV to zero<ref name = "vroom" />. The IRR does not account for the absolute benefits in terms of money, but rather the rate of return that a project or investment generates<ref name = "DSSA"/>. Furthermore, an advantage of the IRR tool is that it presents the merit of avoiding any immediate choice of a discount rate, as the discount rate in the IRR is determined by the stream of cash flows generated by an investment or project, rather than an external discount rate. This makes this tool highly useful when ranking multiple projects or investments with different discount rates or where the discount rate is inconclusive<ref name = "vroom" />. | ||
| + | |||
| + | * '''[[Wikipedia: Benefit cost ratio | Benefit cost ratio (BCR)]]''' is predominately used in a cost-benefit analysis and expresses the relationship between the discounted potential benefits and discounted relative costs of a proposed investment or project. It is expressed in qualitative terms and does not account for the total economic value to be obtained, but rather the viability of a project or investment<ref name = "BCR" />. If the BCR is greater than 1, it usually correlates with a positive NPV and the project or investment can be regarded as feasible. | ||
| + | |||
| + | * '''[[Wikipedia: Payback period | Payback period (PBP)]]''' is a financial metric that computes the time needed, usually expressed in years, to recuperate an investment. In the process, a break-even point of the investment is established. For the calculation of the PBP, cash flows are used. It is commonly used to evaluate the risk and return of a project or investment. One thing to be mindful of is that PBP as a concept does not account for the time value of money nor opportunity costs<ref name = "PBP" />. | ||
| + | |||
| + | * '''[[Wikipedia: Cost-benefit analysis| Cost-benefit analysis (CBA)]]''' is a broader framework for comparing the benefits and related costs of a project or investment and ranking alternative investments. Central to the CBA analysis, are the concepts of consumer surplus and welfare theory. It is widely applicable in projects or investments that are of socio-economic nature like public infrastructure or transport projects<ref name = "vroom" />. The CBA analysis seeks to identify and quantify all social implications into absolute monetary measures of the social profitability of a project or investment. This accounts for both monetary and non-monetary costs and benefits<ref name ="DSSA" />. The NPV is of the key tools when carrying out a CBA analysis of a project or investment. | ||
| + | |||
| + | Each tool provides unique insights into the profitability of an investment or project and can be applied in conjunction to provide a more comprehensive understanding. Doing so might uncover possible clues to improve the investment or project itself as well as the financial appraisal. In general, when carrying out financial appraisals of projects and investments, with one or more tools mentioned above, conducting a sensitivity analysis is considered good practice. This is due to the element of uncertainty associated with forecasts of any kind since the future is inherently uncertain<ref name = "DSSA" />. | ||
| + | |||
| + | A '''[[Wikipedia: Sensitivity analysis | Sensitivity analysis]]''' aims to highlight distinct variables of projects and investments with significant influence. By investigating how small changes to these distinct values and estimates would affect the outcome of the financial appraisal, decision-makers can get an indication of how robust their appraisal is towards uncertainty and risks DSSA. For instance, if the NPV of a project is highly sensitive to small changes in cost and benefits estimates, this would indicate that choice of estimates needs to be carefully considered. Conversely, if the NPV is not affected in a significant way, it can be considered a more robust estimate<ref name = "vroom" />. | ||
| + | |||
| + | == Application and decision making == | ||
| + | The net present value (NPV) is a financial metric that indicates whether a proposed investment or project is profitable or not. It does so, by aggregating estimated streams of costs and benefits into a single number<ref name = "DSSA" />. For the project or investment to be considered profitable, the NPV must be greater than one. In the assessment of mutually exclusive projects, the NPV provides a precise ranking of alternatives, if the discount rate is unambiguously determined<ref name = "vroom" />. In the assessment of multiple projects sharing interdependences, there must be an analysis of how benefits and costs are affected when projects enter a combination with other projects, e.g., programs and portfolios<ref name ="DSSA" />. A sensible factor to the NPV is the time period of analysis. Many projects or investments, like infrastructure projects, impose a negative cash flow in the first couple of years due to construction costs, before realizing a positive cash flow in the form of benefits. Moreover, the discount factor modulated by the discount rate also influences the choice of the time period. A decision tree consolidating the decision rules for the NPV value is shown in table 2 below: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+ style="caption-side:bottom; color:black;"|''Table 2: Decision types and decision rules. Own creation. Inspiration drawn from<ref name ="DSSA"/>.'' | ||
| + | |Decision type | ||
| + | |Budget constraints | ||
| + | |Project dependence | ||
| + | |Decision rules | ||
| + | |- | ||
| + | |Acceptance of project or investment | ||
| + | |rowspan="4"| | ||
| + | |rowspan="4"| | ||
| + | |NPV > 0 | ||
| + | |- | ||
| + | |Acceptance or rejection based on circumstances | ||
| + | |NPV = 0 | ||
| + | |- | ||
| + | |Rejection of project or investment | ||
| + | |NPV < 0 | ||
| + | |- | ||
| + | |One of several projects or investments | ||
| + | |Max. NPV | ||
| + | |- | ||
| + | |rowspan="4"|Selection of multiple projects or investments from a pool | ||
| + | |style="text-align: center;"|No | ||
| + | |rowspan="2" style="text-align: center;"|Dependent | ||
| + | |Find possible sets: Max. NPV | ||
| + | |- | ||
| + | |style="text-align: center;"|Yes | ||
| + | |Find feasible sets: Max. NPV | ||
| + | |- | ||
| + | |style="text-align: center;"|No | ||
| + | |rowspan="2" style="text-align: center;"|Interdependent | ||
| + | |Rank alternatives by NPV > 0 | ||
| + | |- | ||
| + | |style="text-align: center;"|Yes | ||
| + | |Rank by use of BCR > 1 | ||
| + | |} | ||
| + | |||
| + | == Examples == | ||
| + | |||
| + | '''Example 1: Simple calculation of the present value (Own creation)''' | ||
| + | |||
| + | Considerating the value of €250.000,00 euro in the year 2023, what's the present value in the year 2028, using a discount rate of 3.5%? | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+ style="caption-side:bottom; color:black;"|''Table 3: Simple calculation of the present value. Own creation.'' | ||
| + | |Year | ||
| + | |style="text-align: right;"|0 | ||
| + | |style="text-align: right;"|1 | ||
| + | |style="text-align: right;"|2 | ||
| + | |style="text-align: right;"|3 | ||
| + | |style="text-align: right;"|4 | ||
| + | |style="text-align: right;"|5 | ||
| + | |- | ||
| + | |Discount factor | ||
| + | |style="text-align: right;"|1 | ||
| + | |style="text-align: right;"|0.97 | ||
| + | |style="text-align: right;"|0.93 | ||
| + | |style="text-align: right;"|0.90 | ||
| + | |style="text-align: right;"|0.87 | ||
| + | |style="text-align: right;"|0.84 | ||
| + | |- | ||
| + | |Present value | ||
| + | |style="text-align: right;"|€250,000.00 | ||
| + | |style="text-align: right;"|€241,546.00 | ||
| + | |style="text-align: right;"|€233,378.00 | ||
| + | |style="text-align: right;"|€225,486.00 | ||
| + | |style="text-align: right;"|€217,861.00 | ||
| + | |style="text-align: right;"|€210,493.00 | ||
| + | |} | ||
| + | |||
| + | The present value of €250,000.00 in the year 2028, using a discount rate of 3.5% is calculated to be €210,493.00 | ||
| + | |||
| + | |||
| + | '''Example 2: Calculation of the NPV of a construction project (Own creation)''' | ||
| + | |||
| + | In the following example, let's consider this hypothetical construction project, Gotta Go Fast 2023, which is a new road going from Borups allé, Nordvest 2400, in Copenhagen to DTU Building 408, Auditorium 413. The construction is estimated to take 3 years, and the opening of the road will be is scheduled to open in year 0. First-year impacts are identified and estimated to be the following: | ||
| + | |||
| + | * Travel time savings (TS): €230,000.00 | ||
| + | * Accidents savings (AS): €70,000.00 | ||
| + | * Emissions improvements (EI): €60,000.00 | ||
| + | |||
| + | The project is estimated to cost €13 million and has maintenance costs of €100.000,00 per year after opening. Furthermore, travel time savings are expected to increase by 1.3% each year, whereas all other impacts are assumed to remain constant. The evaluation period is 25 years, and the discount rate is determined to be 3.56% following the European Commission discount rate for Denmark in February 2023. It is assumed that after the evaluation period, the road will still have value. This value is called the scrap value. The value is the construction cost of $13 million, discounted to the final year of the evaluation period. | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+ style="caption-side:bottom; color:black;"|''Table 4: Financial appraisal of a hypothetical project using the NPV metric. Own creation.'' | ||
| + | |Year | ||
| + | |rowspan="3"| | ||
| + | | -3 | ||
| + | | -2 | ||
| + | | -1 | ||
| + | | 0 | ||
| + | |1 | ||
| + | |2 | ||
| + | |3 | ||
| + | |4 | ||
| + | |5 | ||
| + | |.. | ||
| + | |24 | ||
| + | |- | ||
| + | |Discount factor | ||
| + | |1.11 | ||
| + | |1.07 | ||
| + | |1.04 | ||
| + | | 1 | ||
| + | |0.97 | ||
| + | |0.93 | ||
| + | |0.90 | ||
| + | |0.87 | ||
| + | |0.84 | ||
| + | |.. | ||
| + | |0.43 | ||
| + | |- | ||
| + | |TS | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | 1 | ||
| + | |1.01 | ||
| + | |1.03 | ||
| + | |1.04 | ||
| + | |1.05 | ||
| + | |1.07 | ||
| + | |.. | ||
| + | |1.36 | ||
| + | |- | ||
| + | |Sum of construction cost | ||
| + | | -€ 13,947,763 | ||
| + | | -4,812,805 | ||
| + | | -4,647,359 | ||
| + | | -4,487,600 | ||
| + | |colspan="8"| | ||
| + | |- | ||
| + | |Sum of maintenance cost | ||
| + | | -€ 1,695,764 | ||
| + | |rowspan="5" colspan="3"| | ||
| + | | -100.000 | ||
| + | | - 96.562 | ||
| + | | - 93.242 | ||
| + | | - 90.037 | ||
| + | | - 86.942 | ||
| + | | - 83.953 | ||
| + | |.. | ||
| + | |43,190 | ||
| + | |- | ||
| + | |Scrap value | ||
| + | | € 6,478,616 | ||
| + | |colspan="6"| | ||
| + | |.. | ||
| + | |6,478,616 | ||
| + | |- | ||
| + | |Sum of TS | ||
| + | | € 4,468,483 | ||
| + | | 230,000 | ||
| + | | 224,980 | ||
| + | | 220,070 | ||
| + | |215,268 | ||
| + | | 210,570 | ||
| + | |205,975 | ||
| + | |.. | ||
| + | |135,439 | ||
| + | |- | ||
| + | |Sum of AS | ||
| + | | € 1,187,035 | ||
| + | | 70,000 | ||
| + | | 67,593 | ||
| + | | 65,270 | ||
| + | |63,026 | ||
| + | | 60,859 | ||
| + | | 58,767 | ||
| + | |.. | ||
| + | |30,233 | ||
| + | |- | ||
| + | |Sum of EI | ||
| + | | € 1,017,458 | ||
| + | | 60,000 | ||
| + | |57,937 | ||
| + | | 55,945 | ||
| + | |54,022 | ||
| + | | 52,165 | ||
| + | | 50,362 | ||
| + | |.. | ||
| + | |25,914 | ||
| + | |- | ||
| + | |NPV | ||
| + | | -€ 2,401,933 | ||
| + | |colspan="11"| | ||
| + | |} | ||
| + | |||
| + | The NPV is calculated by aggregating all the discounted costs and benefits, in this particular case being: Construction cost, maintenance cost, travel time savings, accident savings, and emissions improvements. The NPV for the hypothetical project, Gotta Go Fast 2023, has a value of -€2,401,933, which deems the project unprofitable. Therefore, sadly, you cannot expect to see a new road going from Nordvest to DTU being established any time soon. | ||
| + | |||
| + | '''Example 3: Ranking of alternatives of projects (Own creation)''' | ||
| + | |||
| + | In the following example, the global food manufacturer, APPM, seeks to expand its program of sugary sweets with an additional treat for the Scandinavian market. To do so, they have an array of potential production lines to choose from, capable of producing one respective sugary treat in their current factory placed in Sweden. The potential production lines are interdependent, and the program manager applies a univocally discount rate to all the potential investments, when calculating the respective NPVs, seen below in table 5: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+ style="caption-side:bottom; color:black;"|''Table 5: Production lines and the respective NPVs. Own creation.'' | ||
| + | |Production line | ||
| + | |Producing | ||
| + | |NPV | ||
| + | |- | ||
| + | |1 | ||
| + | |Liquorice Dinosaurs | ||
| + | |style="text-align: right;"|€ 841,568 | ||
| + | |- | ||
| + | |2 | ||
| + | |Cinnamon Caramel Lollipops | ||
| + | |style="text-align: right;"|€158,381 | ||
| + | |- | ||
| + | |3 | ||
| + | |Taco Flavoured Gummy Bears | ||
| + | | -€150,349 | ||
| + | |- | ||
| + | |4 | ||
| + | |Bacon Marshmallows | ||
| + | |style="text-align: right;"| €596,283 | ||
| + | |} | ||
| + | |||
| + | Based on the NPVs for the respective production lines, APPM decides to commence the establishment of production line 1, producing Liquorice Dinosaurs. Production line 3, is disregarded due to a negative NPV. The other alternatives have positive NPVs, and in theory both are profitable. Although, the final choice is production line 1, since it has the highest NPV. | ||
== Advantages == | == Advantages == | ||
| + | The NPV is cemented as one of the most accurate and used investment criteria amongst financial metrics when it comes to assessing the viability of projects, programs, and portfolios. This is especially true in the financial appraisal process of public investments<ref name = "DSSA" />. There are several reasons for this, and some of them are listed below: | ||
| + | |||
| + | * The NPV accounts for the time value of money through the use of a discount factor, which discounts all future benefits and costs for a proposed investment or project. | ||
| + | |||
| + | * The NPV is expressed as a single absolute metric indicating the profitability of a project or investment, which makes for easy comparison of multiple projects or investments<ref name ="article7" />. | ||
| + | |||
| + | * The NPV method can be applied to assess projects, programs, and portfolios. The two latter are found by aggregating the respective projects within the respective demarcation<ref name ="article7" />. | ||
| + | |||
| + | * A scientifically validated financial metric facilitating impartiality evaluations of projects or investments<ref name = "NPV_P"/>. | ||
== Disadvantages == | == Disadvantages == | ||
| + | The NPV method is not without limitations. A few examples are listed below. | ||
| + | |||
| + | *The accuracy of the NPV is highly dependent on the forecasts estimating the cash flows concerning both the costs and benefits of a proposed project. If the forecast is plagued with high uncertainty, certainly, using the NPV method as a decision tool in financial appraisals is of high uncertainty<ref name ="article7" />. | ||
| + | |||
| + | * The NPV is greatly influenced by the choice of discount rate. Selecting an appropriate discount rate is not an easy task. Selecting a discount rate that is too low, might lead to an inflated NPV index while selecting a discount rate that is too high, might undervalue the profitability of a project, potentially leading to the disregard of that project. | ||
| + | |||
| + | *When assessing multiple interdependent or mutually exclusive projects using the NPV method, big projects are favored in terms of ranking the alternatives<ref name = "vroom" />. | ||
| + | |||
| + | == Annotated Bibliography == | ||
| + | '''Ferarri, C., Conti, M., Bottasso, A., & Tei, A. (2019). Economic Role of Transport Infrastructure: Theory and Models. In Elsevier. https://doi.org/10.1016/b978-0-12-813096-4.01001-5''' | ||
| + | |||
| + | Chapter 5 of the book gives a thorough introduction to the theory and models of financial appraisals. It provides the necessary framework for executing appraisals and provides a comprehensive understanding of the net present value, Internal rate of return, discount rate, and Cost Benefit Analysis. Moreover, the chapter discusses the different situations in which the NPV method is applicable. It addresses the advantages and disadvantages of NPV, and how the latter can be mitigated in juxtaposition with other financial metrics. | ||
| + | |||
| + | '''Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.''' | ||
| + | |||
| + | The compendium written and edited by Michael Bruhn Barfod, Associate Professor at DTU, and Steen Leleur, Professor Emeritus at DTU, gives a comprehensive insight into the appraisal process of infrastructure projects. Section 3, regarding investment appraisal, is highly relevant for grasping NPV as a concept, and the crucial role it plays in financial appraisals of projects. The compendium also provides a sequence of reflections in regard to NPV, and how the financial metric can be leveraged in tandem with other financial metrics, to provide a more thorough appraisal of socio-economic projects. | ||
| + | |||
| + | ''' Project Management Institute, Inc. (PMI). (2021). A Guide to the Project Management Body of Knowledge (PMBOK ® Guide) – 7th Edition and The Standard for Project Management. Project Management Institute, Inc. (PMI). Retrieved from | ||
| + | https://app.knovel.com/hotlink/toc/id:kpSPMAGPMP/guide-project-management/guide-project-management ''' | ||
| + | |||
| + | In the following book's section 2, there is a clear emphasis on how financial metrics, such as the NPV, can quantify and measure business value. It is given in the wider context of monitoring projects and ensuring that the project delivery stays aligned with the business case and the benefits realization plans. | ||
| + | |||
| + | '''AXELOS. Managing Successful Projects with PRINCE2 2017 Edition. London: The Stationery Office Ltd, 2017. Accessed May 2, 2023. ProQuest Ebook Central.''' | ||
| + | |||
| + | In the following book, there is a continuous emphasis on the importance of projects meeting an actual business need and providing value for money. According to PRINCE2, the business perspective is one of three principal project interests, which come together to ensure the success of a project. The book cements the purpose of assessing projects through the lens of a business perspective, to implement mechanisms to decide whether the project is profitable, and viable and can aid decision-making regarding investment. The book gives a few examples of the mechanisms, which include NPV. | ||
| + | |||
| + | == References == | ||
| + | |||
| + | <references> | ||
| + | |||
| + | <ref name="DSSA"> Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.</ref> | ||
| + | |||
| + | <ref name="TVM"> Gardner, N.D. 2004. The Time Value of Money: A Clarifying and Simplifying Approach. Journal of College Teaching & Learning (TLC). 1, 7 (Jul. 2004).</ref> | ||
| + | |||
| + | <ref name ="NPV_H"> Häcker, J., & Ernst, D. (2017). Financial Modeling, Global Financial Markets. 343-384. </ref> | ||
| + | |||
| + | <ref name = "NPV_P"> Žižlavský, O. (2014). Net Present Value Approach: Method for Economic Assessment of Innovation Projects. Procedia - Social and Behavioral Sciences, 156(April), 506–512. </ref> | ||
| + | |||
| + | <ref name = "DISCOUNT"> Office for Budget Responsibility. (2023). Discount rates. https://obr.uk/box/discount-rates/ </ref> | ||
| + | |||
| + | <ref name = "CHAPTER8"> Groth, C. (2014). Lecture notes in Economies. Københans Universitet. 107-131. </ref> | ||
| + | |||
| + | <ref name = "EU"> The Commission of the European Communities. (2023). Reference and discount rates (in %) since 01.08.1997. https://competition-policy.ec.europa.eu/state-aid/legislation/reference-discount-rates-and-recovery-interest-rates/reference-and-discount-rates_en </ref> | ||
| + | |||
| + | <ref name = "WACC"> Hargrave, M. (2022). Weighted Average Cost of Capital ( WACC ) Explained with Formula and Example Learn why a higher WACC is something to watch out for. Investopedia. https://www.investopedia.com/terms/w/wacc.asp </ref> | ||
| + | |||
| + | <ref name = "APM"> Dalcher, D. (2019). APM Body of Knowledge (Seventh ed). Association for Project Management. </ref> | ||
| + | |||
| + | <ref name = "BCR"> Hayes, A. (2022). Benefit-Cost Ratio (BCR): Definition, Formula, and Example. Investopedia. https://www.investopedia.com/terms/b/bcr.asp </ref> | ||
| + | |||
| + | <ref name = "PBP"> Hayes, A. (2022). Reniers, G., Talarico, L., & Paltrinieri, N. (2016). Cost-Benefit Analysis of Safety Measures. In Dynamic Risk Analysis in the Chemical and Petroleum Industry: Evolution and Interaction with Parallel Disciplines in the Perspective of Industrial Application. Elsevier Inc. https://doi.org/10.1016/B978-0-12-803765-2.00016-0 </ref> | ||
| + | |||
| + | <ref name = "TVM1"> Abor, J. Y. (2017). Entrepreneurial Finance for MSMEs. In Entrepreneurial Finance for MSMEs. Springer International Publishing. https://doi.org/10.1007/978-3-319-34021-0 </ref> | ||
| + | |||
| + | <ref name = "TVM2"> Peterson Drake, P., & J. Fabozzi., F. (2009). Foundations and Applications of the Time Value of Money. John Wiley & Sons, Inc. </ref> | ||
| + | |||
| + | <ref name = "vroom"> Ferarri, C., Conti, M., Bottasso, A., & Tei, A. (2019). Economic Role of Transport Infrastructure: Theory and Models. In Elsevier. </ref> | ||
| + | |||
| + | <ref name = "article7"> Bora, D. B. (2015). ABSTRACT : Review of literature : International Journal of Research in Finance and Marketing, 5(12), 61–71. http://onlinelibrary.wiley.com/doi/10.1111/j.1745-6622.2002.tb00337.x/full </ref> | ||
Latest revision as of 12:50, 5 May 2023
Contents |
[edit] Abstract
The Net Present Value (NPV) is a widely used financial metric in project management. Its purpose is to evaluate the profitability of a proposed project by aggregating the streams of costs and benefits into a single value. This makes for an effective indicator of identifying profitable projects when assessing multiple projects at a time. For a given project to be considered a profitable investment, its NPV must be larger than zero[1].
Central to the calculation of the NPV is assigning varying weights, dependent on time, to the benefits and costs through the utilization of a so-called discount factor, which is calculated using a discount rate. The discount rate represents the rate of interest that is used to discount all future costs and benefits[1]. By incorporating this principle, the NPV accounts for and subscribes to the paradigm of the time value of money, referring to the idea that money has a different value at different points in time[2].
This article explores central concepts connected to the calculation and application of NPV in the assessment of projects, programs, or portfolios. Moreover, how it relates to financial appraisals of projects and how it can support decision-makers in the process of doing so. For demonstration purposes, an example of the calculation of an emulated project's NPV will be given. Moreover, the advantages and disadvantages of using NPV as an indicator of project profitability will be addressed.
[edit] NPV Formula
The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments[3]. The formula used to calculate the net present value is presented below:
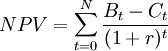
where
-
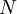 : The calculation period of the project in years.
: The calculation period of the project in years.
-
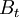 : The aggregated amount of benefits (both positive and negative) in year t
: The aggregated amount of benefits (both positive and negative) in year t
-
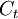 : The amount of investments costs in year t
: The amount of investments costs in year t
-
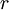 : The discount rate
: The discount rate
There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain euro tomorrow is less valuable than a euro today[4]. This is modulated by the use of the discount factor 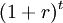 , where a discount rate is used[1]. Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to
, where a discount rate is used[1]. Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to 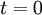 . The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon,
. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, 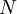 [4]. For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value.
[4]. For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value.
[edit] Time value of money
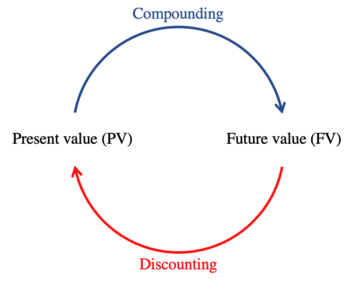
Central to understanding the financial viability of future projects or investments is the concept of the time value of money (TVM). TVM deals with the truth that a euro today is worth more than a euro tomorrow[6]. The promise of any future amount of money is affiliated with a certain degree of uncertainty, some promises are riskier than others. This means that it requires a larger sum of future euros than current euros to purchase the same number of services and goods today. Furthermore, it begs the question that receiving a specified amount of euros today, rather than later, gives the opportunity to invest the money in order to yield interest. Moving money through time involves interest as a medium to translate the values from one period to another[5]. Interest can be perceived as the price of the risk and the price of the time of the resources borrowed. The risk component is the uncertainty of whether the lender is able to recuperate the initial amount from which was borrowed. To see the concept illustrated, please refer to Figure 1. The time component is the possibility of spending resources differently. Compound interest refers to the process of the time value of money over numerous periods influenced by interest[5]. In simple terms, if a company were to borrow €500,000.00 for a project with an expected annual compound interest rate of 1.5%, after 1 year the payback amount would be €507,500.00, and after 10 years the amount would be €580,270.41. Therefore, the time horizon, interest rate, and the sum of the invested money are pivotal in determining the future value of an investment or project.
[edit] Discount rate
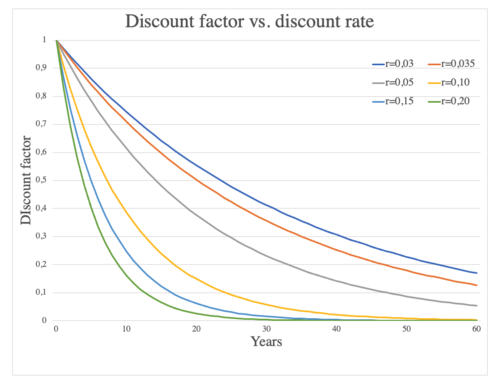
The discount rate is the interest rate to convert future cash flows into an equivalent one-off upfront sum or present value [7]. As the discount rate increases, the lower the present value of a given future amount becomes. Hence the magnitude of the discount rate exerts a significant influence on the net present value. For instance, if the selected discount rate level is set too high, it may make potentially good projects, programs or portfolios seem unattractive, whereas if set too low, it might result in the opposite. To see how different discount rates modulate the discount factor, thus influencing the NPV of a given project, see Figure 2.
[edit] Selection of discount rate
The selection of an appropriate discount rate can be a very exhaustive and challenging task, as the decision is dependent on multiple factors, to name a few:
- The situational circumstances under which the investment project is taking place are characterized by fundamental uncertainty, computable risk, or certainty. The first, driving the discount rate to increase the most[8]. Furthermore, the jurisdiction and location of the project being commenced also play a role in the choice of a discount rate[9].
- The duration of the time horizon, especially in a socio-economic context, numerous countries have opted to differentiate between projects that span less than or more than 30-50 years, with the latter receiving a lower discount rate[8].
- Private versus public and government bodies. Discounting from a firm’s or individual perspective is inherently different than that of government bodies[8].
In relation to state-aided projects, the European Commission calculates and issues base rates each month for countries within the union. The discount rate can be found by adding a margin of a 100 basispoints to the base rate. The base rate for the first four months of 2023 is depicted in table 1.
| Base rates as of 1.4.2023 | |||||||||||||||||||||||||||||
| From | To | AT | BE | BG | CY | CZ | DE | DK | EE | EL | ES | FI | FR | HR | HU | IE | IT | LT | LU | LV | MT | NL | PL | PT | RO | SE | SI | SK | UK |
| 1.4.2023 | … | 3.06 | 3.06 | 1.51 | 3.06 | 7.43 | 3.06 | 3.54 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 15.10 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 7.62 | 3.06 | 8.31 | 3.21 | 3.06 | 3.06 | 3.52 |
| 1.3.2023 | 31.3.2023 | 3.06 | 3.06 | 1.10 | 3.06 | 7.43 | 3.06 | 2.92 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 15.10 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 3.06 | 7.62 | 3.06 | 8.31 | 2.96 | 3.06 | 3.06 | 3.52 |
| 1.2.2023 | 28.2.2023 | 2.56 | 2.56 | 0.79 | 2.56 | 7.43 | 2.56 | 2.92 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 15.10 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 7.62 | 2.56 | 8.31 | 2.44 | 2.56 | 2.56 | 2.77 |
| 1.1.2023 | 31.1.2023 | 2.56 | 2.56 | 0.36 | 2.56 | 7.43 | 2.56 | 2.92 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 15.10 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 2.56 | 7.62 | 2.56 | 8.31 | 2.44 | 2.56 | 2.56 | 2.77 |
The weighted average cost of capital (WACC) is another way to determine and select an appropriate discount rate for firms, in the appraisal process of a proposed investment or project using the NPV. The WACC represents the risk to the future cashflows received by an organization from its operations including equity and debt. It weighs the cost of each capital source by its relevant weight by market value and adds it together to determine the total. The gist of using the WACC besides it representing a minimum rate of return that a firm must achieve is that it can be used as a proxy for a suitable discount rate [10]. The WACC is calculated as follows[10]:
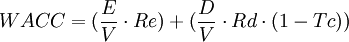
Where
-
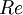 : Cost of equity
: Cost of equity
-
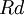 : Cost of debt
: Cost of debt
-
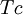 : Corporate tax rate
: Corporate tax rate
-
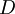 : Market value of the company's debt
: Market value of the company's debt
-
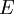 : Market value of the company's equity
: Market value of the company's equity
-
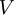 =
= 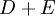
To summarize, the choice of discount rate has a tremendous impact on the appraisal outcome of investments or projects using the NPV[1]. To a high extent, the selection of the discount rate is dependent on the context in which it is used. Therefore, one must be aware of the circumstances, the type of project, and the affiliated risk that the very project or investment comes with. In its most basic shape, the discount rate simply gives an insight into how profitable a future project or investment can be for a particular organization.
[edit] Financial Appraisal
The gist of financial appraisals is to deliver the maximum value for money of a project for the project implementor. Moreover, to determine the viability of the investment or project by assessing the future net cash flow as a result of the realization[11]. The financial appraisal is a systematic process for analyzing alternative uses of limited assets and resources. It focuses on the assessment of benefits, costs, objectives, risks, funding, and executability. The financial appraisal facilities great management practices and it is vital to create transparency, and accountability, and make informed decisions. Financial appraisals are a difficult matter, yet an important tool, even an imperfect one, that makes it possible to compare options on a project, program, and portfolio level. It can be complemented by a business case, that takes the wider narrative into account on how that said the investment could be executed to realize the intended benefits[11]. There are plenty of tools to choose from besides the NPV, the common nominator being comparability, such as the:
- Internal rate of return (IRR) aims to determine the rate i, balancing the cost and benefit streams, simply put the rate i that equals NPV to zero[12]. The IRR does not account for the absolute benefits in terms of money, but rather the rate of return that a project or investment generates[1]. Furthermore, an advantage of the IRR tool is that it presents the merit of avoiding any immediate choice of a discount rate, as the discount rate in the IRR is determined by the stream of cash flows generated by an investment or project, rather than an external discount rate. This makes this tool highly useful when ranking multiple projects or investments with different discount rates or where the discount rate is inconclusive[12].
- Benefit cost ratio (BCR) is predominately used in a cost-benefit analysis and expresses the relationship between the discounted potential benefits and discounted relative costs of a proposed investment or project. It is expressed in qualitative terms and does not account for the total economic value to be obtained, but rather the viability of a project or investment[13]. If the BCR is greater than 1, it usually correlates with a positive NPV and the project or investment can be regarded as feasible.
- Payback period (PBP) is a financial metric that computes the time needed, usually expressed in years, to recuperate an investment. In the process, a break-even point of the investment is established. For the calculation of the PBP, cash flows are used. It is commonly used to evaluate the risk and return of a project or investment. One thing to be mindful of is that PBP as a concept does not account for the time value of money nor opportunity costs[14].
- Cost-benefit analysis (CBA) is a broader framework for comparing the benefits and related costs of a project or investment and ranking alternative investments. Central to the CBA analysis, are the concepts of consumer surplus and welfare theory. It is widely applicable in projects or investments that are of socio-economic nature like public infrastructure or transport projects[12]. The CBA analysis seeks to identify and quantify all social implications into absolute monetary measures of the social profitability of a project or investment. This accounts for both monetary and non-monetary costs and benefits[1]. The NPV is of the key tools when carrying out a CBA analysis of a project or investment.
Each tool provides unique insights into the profitability of an investment or project and can be applied in conjunction to provide a more comprehensive understanding. Doing so might uncover possible clues to improve the investment or project itself as well as the financial appraisal. In general, when carrying out financial appraisals of projects and investments, with one or more tools mentioned above, conducting a sensitivity analysis is considered good practice. This is due to the element of uncertainty associated with forecasts of any kind since the future is inherently uncertain[1].
A Sensitivity analysis aims to highlight distinct variables of projects and investments with significant influence. By investigating how small changes to these distinct values and estimates would affect the outcome of the financial appraisal, decision-makers can get an indication of how robust their appraisal is towards uncertainty and risks DSSA. For instance, if the NPV of a project is highly sensitive to small changes in cost and benefits estimates, this would indicate that choice of estimates needs to be carefully considered. Conversely, if the NPV is not affected in a significant way, it can be considered a more robust estimate[12].
[edit] Application and decision making
The net present value (NPV) is a financial metric that indicates whether a proposed investment or project is profitable or not. It does so, by aggregating estimated streams of costs and benefits into a single number[1]. For the project or investment to be considered profitable, the NPV must be greater than one. In the assessment of mutually exclusive projects, the NPV provides a precise ranking of alternatives, if the discount rate is unambiguously determined[12]. In the assessment of multiple projects sharing interdependences, there must be an analysis of how benefits and costs are affected when projects enter a combination with other projects, e.g., programs and portfolios[1]. A sensible factor to the NPV is the time period of analysis. Many projects or investments, like infrastructure projects, impose a negative cash flow in the first couple of years due to construction costs, before realizing a positive cash flow in the form of benefits. Moreover, the discount factor modulated by the discount rate also influences the choice of the time period. A decision tree consolidating the decision rules for the NPV value is shown in table 2 below:
| Decision type | Budget constraints | Project dependence | Decision rules |
| Acceptance of project or investment | NPV > 0 | ||
| Acceptance or rejection based on circumstances | NPV = 0 | ||
| Rejection of project or investment | NPV < 0 | ||
| One of several projects or investments | Max. NPV | ||
| Selection of multiple projects or investments from a pool | No | Dependent | Find possible sets: Max. NPV |
| Yes | Find feasible sets: Max. NPV | ||
| No | Interdependent | Rank alternatives by NPV > 0 | |
| Yes | Rank by use of BCR > 1 |
[edit] Examples
Example 1: Simple calculation of the present value (Own creation)
Considerating the value of €250.000,00 euro in the year 2023, what's the present value in the year 2028, using a discount rate of 3.5%?
| Year | 0 | 1 | 2 | 3 | 4 | 5 |
| Discount factor | 1 | 0.97 | 0.93 | 0.90 | 0.87 | 0.84 |
| Present value | €250,000.00 | €241,546.00 | €233,378.00 | €225,486.00 | €217,861.00 | €210,493.00 |
The present value of €250,000.00 in the year 2028, using a discount rate of 3.5% is calculated to be €210,493.00
Example 2: Calculation of the NPV of a construction project (Own creation)
In the following example, let's consider this hypothetical construction project, Gotta Go Fast 2023, which is a new road going from Borups allé, Nordvest 2400, in Copenhagen to DTU Building 408, Auditorium 413. The construction is estimated to take 3 years, and the opening of the road will be is scheduled to open in year 0. First-year impacts are identified and estimated to be the following:
- Travel time savings (TS): €230,000.00
- Accidents savings (AS): €70,000.00
- Emissions improvements (EI): €60,000.00
The project is estimated to cost €13 million and has maintenance costs of €100.000,00 per year after opening. Furthermore, travel time savings are expected to increase by 1.3% each year, whereas all other impacts are assumed to remain constant. The evaluation period is 25 years, and the discount rate is determined to be 3.56% following the European Commission discount rate for Denmark in February 2023. It is assumed that after the evaluation period, the road will still have value. This value is called the scrap value. The value is the construction cost of $13 million, discounted to the final year of the evaluation period.
| Year | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | .. | 24 | |
| Discount factor | 1.11 | 1.07 | 1.04 | 1 | 0.97 | 0.93 | 0.90 | 0.87 | 0.84 | .. | 0.43 | |
| TS | 1 | 1.01 | 1.03 | 1.04 | 1.05 | 1.07 | .. | 1.36 | ||||
| Sum of construction cost | -€ 13,947,763 | -4,812,805 | -4,647,359 | -4,487,600 | ||||||||
| Sum of maintenance cost | -€ 1,695,764 | -100.000 | - 96.562 | - 93.242 | - 90.037 | - 86.942 | - 83.953 | .. | 43,190 | |||
| Scrap value | € 6,478,616 | .. | 6,478,616 | |||||||||
| Sum of TS | € 4,468,483 | 230,000 | 224,980 | 220,070 | 215,268 | 210,570 | 205,975 | .. | 135,439 | |||
| Sum of AS | € 1,187,035 | 70,000 | 67,593 | 65,270 | 63,026 | 60,859 | 58,767 | .. | 30,233 | |||
| Sum of EI | € 1,017,458 | 60,000 | 57,937 | 55,945 | 54,022 | 52,165 | 50,362 | .. | 25,914 | |||
| NPV | -€ 2,401,933 | |||||||||||
The NPV is calculated by aggregating all the discounted costs and benefits, in this particular case being: Construction cost, maintenance cost, travel time savings, accident savings, and emissions improvements. The NPV for the hypothetical project, Gotta Go Fast 2023, has a value of -€2,401,933, which deems the project unprofitable. Therefore, sadly, you cannot expect to see a new road going from Nordvest to DTU being established any time soon.
Example 3: Ranking of alternatives of projects (Own creation)
In the following example, the global food manufacturer, APPM, seeks to expand its program of sugary sweets with an additional treat for the Scandinavian market. To do so, they have an array of potential production lines to choose from, capable of producing one respective sugary treat in their current factory placed in Sweden. The potential production lines are interdependent, and the program manager applies a univocally discount rate to all the potential investments, when calculating the respective NPVs, seen below in table 5:
| Production line | Producing | NPV |
| 1 | Liquorice Dinosaurs | € 841,568 |
| 2 | Cinnamon Caramel Lollipops | €158,381 |
| 3 | Taco Flavoured Gummy Bears | -€150,349 |
| 4 | Bacon Marshmallows | €596,283 |
Based on the NPVs for the respective production lines, APPM decides to commence the establishment of production line 1, producing Liquorice Dinosaurs. Production line 3, is disregarded due to a negative NPV. The other alternatives have positive NPVs, and in theory both are profitable. Although, the final choice is production line 1, since it has the highest NPV.
[edit] Advantages
The NPV is cemented as one of the most accurate and used investment criteria amongst financial metrics when it comes to assessing the viability of projects, programs, and portfolios. This is especially true in the financial appraisal process of public investments[1]. There are several reasons for this, and some of them are listed below:
- The NPV accounts for the time value of money through the use of a discount factor, which discounts all future benefits and costs for a proposed investment or project.
- The NPV is expressed as a single absolute metric indicating the profitability of a project or investment, which makes for easy comparison of multiple projects or investments[15].
- The NPV method can be applied to assess projects, programs, and portfolios. The two latter are found by aggregating the respective projects within the respective demarcation[15].
- A scientifically validated financial metric facilitating impartiality evaluations of projects or investments[4].
[edit] Disadvantages
The NPV method is not without limitations. A few examples are listed below.
- The accuracy of the NPV is highly dependent on the forecasts estimating the cash flows concerning both the costs and benefits of a proposed project. If the forecast is plagued with high uncertainty, certainly, using the NPV method as a decision tool in financial appraisals is of high uncertainty[15].
- The NPV is greatly influenced by the choice of discount rate. Selecting an appropriate discount rate is not an easy task. Selecting a discount rate that is too low, might lead to an inflated NPV index while selecting a discount rate that is too high, might undervalue the profitability of a project, potentially leading to the disregard of that project.
- When assessing multiple interdependent or mutually exclusive projects using the NPV method, big projects are favored in terms of ranking the alternatives[12].
[edit] Annotated Bibliography
Ferarri, C., Conti, M., Bottasso, A., & Tei, A. (2019). Economic Role of Transport Infrastructure: Theory and Models. In Elsevier. https://doi.org/10.1016/b978-0-12-813096-4.01001-5
Chapter 5 of the book gives a thorough introduction to the theory and models of financial appraisals. It provides the necessary framework for executing appraisals and provides a comprehensive understanding of the net present value, Internal rate of return, discount rate, and Cost Benefit Analysis. Moreover, the chapter discusses the different situations in which the NPV method is applicable. It addresses the advantages and disadvantages of NPV, and how the latter can be mitigated in juxtaposition with other financial metrics.
Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.
The compendium written and edited by Michael Bruhn Barfod, Associate Professor at DTU, and Steen Leleur, Professor Emeritus at DTU, gives a comprehensive insight into the appraisal process of infrastructure projects. Section 3, regarding investment appraisal, is highly relevant for grasping NPV as a concept, and the crucial role it plays in financial appraisals of projects. The compendium also provides a sequence of reflections in regard to NPV, and how the financial metric can be leveraged in tandem with other financial metrics, to provide a more thorough appraisal of socio-economic projects.
Project Management Institute, Inc. (PMI). (2021). A Guide to the Project Management Body of Knowledge (PMBOK ® Guide) – 7th Edition and The Standard for Project Management. Project Management Institute, Inc. (PMI). Retrieved from https://app.knovel.com/hotlink/toc/id:kpSPMAGPMP/guide-project-management/guide-project-management
In the following book's section 2, there is a clear emphasis on how financial metrics, such as the NPV, can quantify and measure business value. It is given in the wider context of monitoring projects and ensuring that the project delivery stays aligned with the business case and the benefits realization plans.
AXELOS. Managing Successful Projects with PRINCE2 2017 Edition. London: The Stationery Office Ltd, 2017. Accessed May 2, 2023. ProQuest Ebook Central.
In the following book, there is a continuous emphasis on the importance of projects meeting an actual business need and providing value for money. According to PRINCE2, the business perspective is one of three principal project interests, which come together to ensure the success of a project. The book cements the purpose of assessing projects through the lens of a business perspective, to implement mechanisms to decide whether the project is profitable, and viable and can aid decision-making regarding investment. The book gives a few examples of the mechanisms, which include NPV.
[edit] References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.
- ↑ Gardner, N.D. 2004. The Time Value of Money: A Clarifying and Simplifying Approach. Journal of College Teaching & Learning (TLC). 1, 7 (Jul. 2004).
- ↑ Häcker, J., & Ernst, D. (2017). Financial Modeling, Global Financial Markets. 343-384.
- ↑ 4.0 4.1 4.2 Žižlavský, O. (2014). Net Present Value Approach: Method for Economic Assessment of Innovation Projects. Procedia - Social and Behavioral Sciences, 156(April), 506–512.
- ↑ 5.0 5.1 5.2 Peterson Drake, P., & J. Fabozzi., F. (2009). Foundations and Applications of the Time Value of Money. John Wiley & Sons, Inc.
- ↑ Abor, J. Y. (2017). Entrepreneurial Finance for MSMEs. In Entrepreneurial Finance for MSMEs. Springer International Publishing. https://doi.org/10.1007/978-3-319-34021-0
- ↑ Office for Budget Responsibility. (2023). Discount rates. https://obr.uk/box/discount-rates/
- ↑ 8.0 8.1 8.2 Groth, C. (2014). Lecture notes in Economies. Københans Universitet. 107-131.
- ↑ 9.0 9.1 The Commission of the European Communities. (2023). Reference and discount rates (in %) since 01.08.1997. https://competition-policy.ec.europa.eu/state-aid/legislation/reference-discount-rates-and-recovery-interest-rates/reference-and-discount-rates_en
- ↑ 10.0 10.1 Hargrave, M. (2022). Weighted Average Cost of Capital ( WACC ) Explained with Formula and Example Learn why a higher WACC is something to watch out for. Investopedia. https://www.investopedia.com/terms/w/wacc.asp
- ↑ 11.0 11.1 Dalcher, D. (2019). APM Body of Knowledge (Seventh ed). Association for Project Management.
- ↑ 12.0 12.1 12.2 12.3 12.4 12.5 Ferarri, C., Conti, M., Bottasso, A., & Tei, A. (2019). Economic Role of Transport Infrastructure: Theory and Models. In Elsevier.
- ↑ Hayes, A. (2022). Benefit-Cost Ratio (BCR): Definition, Formula, and Example. Investopedia. https://www.investopedia.com/terms/b/bcr.asp
- ↑ Hayes, A. (2022). Reniers, G., Talarico, L., & Paltrinieri, N. (2016). Cost-Benefit Analysis of Safety Measures. In Dynamic Risk Analysis in the Chemical and Petroleum Industry: Evolution and Interaction with Parallel Disciplines in the Perspective of Industrial Application. Elsevier Inc. https://doi.org/10.1016/B978-0-12-803765-2.00016-0
- ↑ 15.0 15.1 15.2 Bora, D. B. (2015). ABSTRACT : Review of literature : International Journal of Research in Finance and Marketing, 5(12), 61–71. http://onlinelibrary.wiley.com/doi/10.1111/j.1745-6622.2002.tb00337.x/full