The Critical Path Method in project planning
(→Introduction and purpose of CPM) |
|||
| (261 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | ''' | + | ''Developed by Chalida Jaidee'' |
| − | |||
| − | + | Projects normally include many activities involving lots of different people. Due to this it can be difficult for project managers to have an overview of and keep track of things. In such situation '''The Critical Path Method (CPM)''' can be a useful tool. CPM is a step by step technique that is used to schedule a set of project activities. It analysis what activities are least flexible and the project duration is predicted based on the activities that fall along the critical path. The critical path is the longest sequence of activities in a project plan which must be completed on time in order for the project to complete on the predetermined scheduled date.<ref name=Crit>BusinessDictionary. (2016). ''Critical Path''. Retrieved September 8, 2016, from http://www.businessdictionary.com/definition/critical-path.html.</ref> Delaying an activity on the critical path leads to a delay on the completion time of the entire project as these activities have no slack. Activities along the path cannot start until the predecessor activity is completed. When using CPM to plan a project a graphical diagram is often represented showing how each activity is related to the others.<ref name=Crit2>Webodia. (2016). ''Critical Path Method''. Retrieved September 8, 2016, from http://www.webopedia.com/TERM/C/Critical_Path_Method.html.</ref> This method is one of several tools that is important to keep projects on track and is convenient for all forms of projects, including research projects, product development, construction industry, maintenance and many more. | |
| + | |||
| + | A joint venture between the Dupont chemical company and computer firm Remington Rand Univac led to a development of the Critical Path Method in the 1950's to tackle the interrelationships of separate activities within a project schedule.<ref name=Crit3>Kielmas, M. (2016). ''History of the Critical Path Method''. Retrieved September 8, 2016, from http://smallbusiness.chron.com/history-critical-path-method-55917.html.</ref> | ||
| + | |||
| + | In this article the CPM is described, a step by step guidance on how to apply the method is discussed and the trade-off between cost and time is analysed. Furthermore, a comparison to other project management techniques is performed and its limitations and advantages are addressed. The main focus of this article is to walk the readers through the CPM process step by step with the aim that they will be able to execute the method after reading this article. | ||
| + | |||
= Overview = | = Overview = | ||
| − | == Introduction and purpose of CPM == | + | === Introduction and purpose of CPM === |
| − | [[File:PLife.png|350px|thumb|right|Figure 1: Project life cycle. http://flylib.com/books/en/2.466.1.51/1/]] | + | [[File:PLife.png|350px|thumb|right|Figure 1: Project life cycle.<ref name=LifeCycle>Francis, D., Horine, G. & Tittel, E. (2008). ''The Relationship Between Project Lifecycle and Project Management Processes''. Retrieved September 8, 2016, from http://flylib.com/books/en/2.466.1.51/1/. </ref>]] |
| − | “A project is a temporary endeavor undertaken to create a unique product or service” http://www.cs.bilkent.edu.tr/~cagatay/cs413/PMBOK.pdf | + | ''“A project is a temporary endeavor undertaken to create a unique product or service”''.<ref name=ProdMan>Project Management Institute. (2000). ''A Guide to the Project Management Body of Knowledge''. Pp. 4. Retrieved September 10, 2016, from http://www.cs.bilkent.edu.tr/~cagatay/cs413/PMBOK.pdf. </ref> The major goal of a project is to satisfy customer’s needs and achieve an organizations’s strategic plan. Projects are unique as they are different in some distinguishing way from all other projects. They have a life cycle were the life span is limited and there are predictable changes in level of effort and focus over the life of the projects. Project life cycle generally passes sequentially through four stages: '''defining''', '''planning''', '''executing''' and '''delivering'''. This is illustrated in ''Figure 1''.<ref name=PMbook>Larson, E. W & Gray, C. F. (2011). ''Project Management, the managerial process''. 5th edition, Pp. 3-10, 157-172. USA: NY. ISBN 978-0-07-340334-2.</ref> |
| − | [[File: | + | [[File:Triplecons.png|200px|thumb|left|Figure 2: Triple constraint (also known as the Project Management Triangle).<ref name=Triple>Haughey, D. (2011). ''Understanding the projoect management triple constraint''. Retrieved September 16, 2016, from https://www.projectsmart.co.uk/understanding-the-project-management-triple-constraint.php.</ref>]] |
| − | |||
| − | + | To meet project requirements, it is important to have a good knowledge of project management. ''“If you fail to plan you are planning to fail”'' is a phrase often used. This can be related to project management, which is an application of knowledge, skills and a set of tools that improves the ability to plan, implement, and manage activities to accomplish specific organizational objectives. Not only is project management a set of tools, it is also a result-oriented management style that places a premium on building collaborative relationships among a diverse cast of characters. <ref name=PMbook /> | |
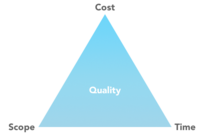
| − | == | + | When managing projects, it is crucial to have a good understanding of the <span class="plainlinks">[https://en.wikipedia.org/wiki/Project_management_triangle Triple constraint]</span> (also known as The Project Management Triangle). These constraints, '''time''', '''scope''' and '''cost''', form a triangle with a '''quality''' in the center as can be seen in ''Figure 2''. They are all fully inter-related, which means that if one side is altered the other two will be affected in some manner. These constraints must be handled effectively for successful completion of any project as well as for the company to meet their customer quality requirements.<ref name=bla>ProgramSucess. (2011). ''Scope, Time and Cost – Managing the Triple Constraint''. Retrieved September 8, 2016, from https://programsuccess.wordpress.com/2011/05/02/scope-time-and-cost-managing-the-triple-constraint/. </ref> In order for this to be fulfilled the CPM technique can be a good assist. |
| − | + | ===History=== | |
| − | + | A Dupont engineer, Morgan R. Walker and a Remington-Rand computer expert, James E. Kelly, Jr. developed the CPM in the 1950'. They created a unique way of representing the operations in the system, which involved using unique arrow filled diagrams. At the similar time, the U.S. Navy initiated a project called Program Evaluation Research Task (<span class="plainlinks">[https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique PERT]</span>). The purpose of that was to provide naval management with an effective manner by which they could periodically evaluate the information of the new Fleet Ballistic Missile program. With this the US Navy could obtain valid information of the project's progress and also have a reasonable accurate projection of the completion of the project as desired. It is worth mentioning that PERT does not include the quantity, quality and cost information, it only deals with the time constraints.<ref name=disadv1 /> PERT-CPM was a successful tool for the hardware-oriented programs, but its application in resource management problems was limited. As CPM techniques were modified and designed to operate on the smaller new computer systems, they proved useful in smaller projects such as design and marketing of new products, maintenance and shutdown schedules, and research and development programs.<ref name=adv1 /> | |
| − | + | Today, there are several project management softwares that can be chosen to execute the CPM in complex projects, such as Microsoft project. Despite that, it is important as a project manager to have an understanding of how to apply the CPM techniques by hand. | |
| − | + | =General methodology= | |
| − | CPM calculates the longest path of planned activities to logical end points or to the end of the project, as well as the earliest and latest that each activity can start and finish without | + | CPM is an algorithm for scheduling a set of activities. It calculates the longest path of planned activities to logical end points or to the end of the project, as well as the earliest and latest that each activity can start and finish without increasing the project duration. This process determines which activities are critical (i.e. on the longest path) and which have slack (i.e. can be delayed without increasing the project duration). Critical path is a sequence of project network activities which ass up to the longest overall duration. It determines the shortest time possible to complete the project. Any delay of an activity on the critical path directly impacts the planned project completion date (i.e. there is no slack on the critical path). A project can have several, parallel, near critical paths. An additional parallel path through the network with the total durations shorter than the critical path is called a sub-critical or non-critical path. The sensitivity of the network increases with increasing number of critical paths.<ref name=ProdPlan>Hansen, Z. N. L. (2016). ''Project planning''. Retrieved from CampusNet in course 42459, planning and scheduling in manufacturing services. </ref> |
| − | + | The essential technique for using CPM is to construct a model of the project that includes: | |
| − | *A list of all activities required to complete the project (typically categorised within a work breakdown structure) | + | *A list of all activities required to complete the project (typically categorised within a work breakdown structure). |
| − | *The time (duration) that each activity will take to complete | + | *The time (duration) that each activity will take to complete. |
| − | *The dependencies between the activities | + | *The dependencies between the activities. |
| − | *Creation of the network diagram based on the activities, dependencies and | + | *Creation of the network diagram based on the activities, dependencies and durations. |
| − | *Logical end points such as milestones or deliverable items | + | *Logical end points such as milestones or deliverable items. |
| − | *Identification of the critical path with | + | *Identification of the critical path with three steps: |
| − | + | #Forward pass procedure | |
| − | + | #Backward pass procedure | |
| − | *Follow up and regular update of the network diagram when there is a change in the project | + | #Slack computation |
| + | *Follow up and regular update of the network diagram when there is a change in the project. | ||
=Application= | =Application= | ||
| − | To get a deeper understanding of the application of CPM a detailed description | + | To get a deeper understanding of the application of CPM a detailed description will be presented step by step in this section with an example. |
| − | ==CPM | + | ===CPM node layout=== |
| − | The CPM network consist of CPM | + | The CPM network consist of CPM nodes for each and every activity. The number of the nodes in each network is dependent on the size of the project. The layout can be seen in ''Figure 3''. To make the layout complete following informations must be filled out in the graph box: |
| − | [[File:Graphbox.png|500px|thumb|right|Figure 3: | + | [[File:Graphbox.png|500px|thumb|right|Figure 3: Node layout for a project network.]] |
| − | *'''Activity ID''': Each activity has a unique identification number | + | *'''Activity ID''': Each activity has a unique identification number. |
| − | *'''Activity description''': Description of the activity | + | *'''Activity description''': Description of the activity. |
| − | *'''Duration''': The time it takes to complete each activity | + | *'''Duration''': The time it takes to complete each activity. |
| − | *'''ES''': Stands for early start. This is the earliest starting time of an activity | + | *'''ES''': Stands for early start. This is the earliest starting time of an activity. |
| − | *'''EF''': Stands for early finish. This is the earliest finish time of an activity | + | *'''EF''': Stands for early finish. This is the earliest finish time of an activity. |
| − | *'''LS''': Stands for late start. This is the latest starting time of an activity | + | *'''LS''': Stands for late start. This is the latest starting time of an activity. |
| − | *'''LF''': Stands for late finish. This is the latest finish time of an activity | + | *'''LF''': Stands for late finish. This is the latest finish time of an activity. |
| − | *'''SL''': Stands for slack. It represents how long and activity can be delayed without affecting the duration of the project | + | *'''SL''': Stands for slack. It represents how long and activity can be delayed without affecting the duration of the project. |
| − | ==CPM network creation== | + | ===CPM network creation=== |
| − | + | First step in the CPM process is to construct the CPM network, which is developed from the <span class="plainlinks">[https://en.wikipedia.org/wiki/Work_breakdown_structure WBS]</span>. The network is a visual flow diagram of sequence, interrelationship, and dependencies of all the activities that must be accomplished to complete the project. The network is built using nodes and arrows, where the node represents an activity and the arrow shows dependency and project flow.<ref name=PMbook /> | |
| − | Basic rules that apply in general when developing a project network are as follow: | + | Basic rules that apply in general when developing a project network are as follow:<ref name=PMbook /> |
| − | *Networks flow from left to right | + | *Networks flow from left to right. |
| − | *All preceding connected activities must be completed before the following activity can begin | + | *All preceding connected activities must be completed before the following activity can begin. |
| − | *Arrows can cross over each other | + | *Arrows can cross over each other. |
| − | *Each activity should have a unique ID code | + | *Each activity should have a unique ID code. |
| − | *An activity identification number must be larger than | + | *An activity identification number must be larger than any activities that precede it. |
| − | *Recycling through a set of activities cannot occur | + | *Recycling through a set of activities cannot occur. |
| − | *Conditional statements are not allowed | + | *Conditional statements are not allowed. |
| − | A CPM network diagram can be constructed given the following | + | A CPM network diagram can be constructed given the following informations: A list of all activities involved in a project and their descriptions, a list of its precedences for each activity and lastly a list of the duration of each activity. ''Table 1'' is an example of the list of activities that will be used to construct a CPM network diagram in this article.<ref name=PMbook /> |
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | ||
| Line 113: | Line 117: | ||
|} | |} | ||
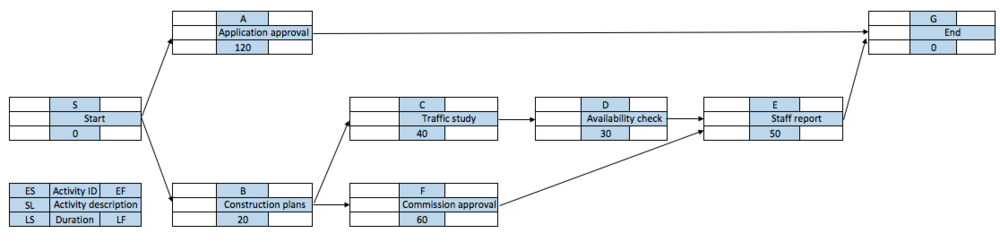
| − | Figure 4 shows the network with the activity time estimates found in the nodes. For example, activity A has an activity duration of 120 | + | By applying the basic rules mentioned here above a network can be constructed as can be seen in ''Figure 4''. It shows the network with the activity time estimates found in the nodes. For example, activity A has an activity duration of 120 days, and activity C has an activity duration of 40 days. These informations are used in the next step called forward pass. |
[[File:network1.png|1000px|thumb|center|Figure 4: Project network.]] | [[File:network1.png|1000px|thumb|center|Figure 4: Project network.]] | ||
| Line 119: | Line 123: | ||
===Forward pass=== | ===Forward pass=== | ||
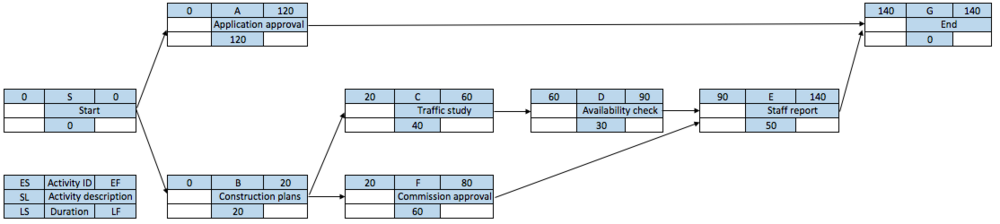
| − | The second step is to calculate the ES, EF and expected normal completion time (TE) by using forward pass computation. This process requires that each path is traced through the network to the last project activity. The longest path denotes the project completion time for the plan and is called the critical path | + | The second step is to calculate the ''ES'', ''EF'' and expected normal completion time ''(TE)'' by using the '''forward pass''' computation. This process requires that each path is traced through the network to the last project activity. The longest path denotes the project completion time for the plan and is called the critical path. There are three steps that are important to keep in mind when using forward pass:<ref name=PMbook /> |
#Activity times are added along each path in the network: '''ES + DUR = EF'''. | #Activity times are added along each path in the network: '''ES + DUR = EF'''. | ||
#The EF is carried to the next activity where it becomes its ES. However, there is one exception which is, | #The EF is carried to the next activity where it becomes its ES. However, there is one exception which is, | ||
| − | #If the next succeeding activity is a '''merge''' | + | #If the next succeeding activity is a '''merge activity''' (activity that has more than one predecessor), the largest EF of all its immediate predecessor activities is selected. |
| − | |||
| − | [[File:FP2.png|1000px|thumb|center|Figure | + | The forward pass begins with the project early start time (ES), which is 0 in this example (activity A and B). This time is found in the upper left corner of the activity nodes in ''Figure 5''. The early finish for activity A is ''120 = 0+120 (ES + DUR = EF)''. The same formula is used to calculate EF for activity B, which resulted in 20 days. Next, it can be seen that activity B is the predecessor for activities C and F. Therefore, the earliest these activities can begin is when activity B is completed. Using the formula mentioned here above the EF can be calculated for all the activities. Reaching to activity E it can be seen that is is a merge activity since it has more than one predecessor. The ES of activity E is controlled by the EF of activities D and F. According to rule no. 3 the largest EF should be selected. Because activity D has higher EF than activity F it controls the ES of activity E, therefore ES for activity E is 90 days. The EF for activity E is 140 days, which is the earliest the project can be expected to complete(TE) under normal conditions. Now since ES, EF and TE is known the next step is to move to the backward pass process. |
| + | |||
| + | [[File:FP2.png|1000px|thumb|center|Figure 5: Project network forward pass.]] | ||
===Backward pass=== | ===Backward pass=== | ||
| − | The third step, the backward pass is similar to the forward pass, except for it requires that the start point is from the last project activity(ies) and each path is traced backward to find LS and LF for each activity. There are three things that are important to keep in mind when using the backward pass process: | + | The third step, the '''backward pass''' is similar to the forward pass, except for it requires that the start point is from the last project activity(ies) and each path is traced backward to find ''LS'' and ''LF'' for each activity. There are three things that are important to keep in mind when using the backward pass process:<ref name=PMbook /> |
#Activity times are subtracted along each path starting with the project end activity: '''LF – DUR = LS'''. | #Activity times are subtracted along each path starting with the project end activity: '''LF – DUR = LS'''. | ||
| − | #LS is carried to the next preceding activity to establish its LF. However, there is one exception | + | #LS is carried to the next preceding activity to establish its LF. However, there is one exception which is, |
#If the next preceding activity is a '''burst''' activity (activity that has more than one successor), the smallest LS of all its immediate successor activities is selected to establish its LF. | #If the next preceding activity is a '''burst''' activity (activity that has more than one successor), the smallest LS of all its immediate successor activities is selected to establish its LF. | ||
| − | Before the backward pass can be computed, LF for the last activity(ies) must be selected. This time is usually set | + | |
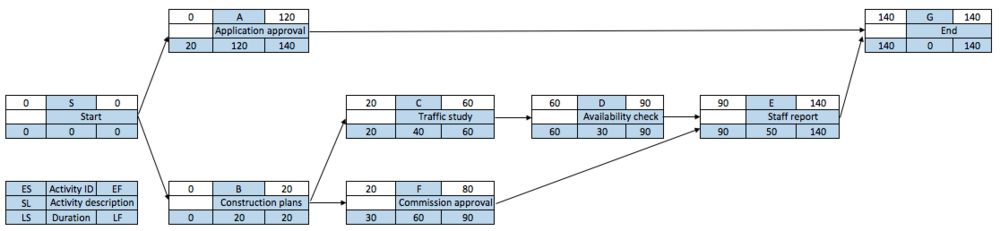
| + | Before the backward pass can be computed, LF for the last activity(ies) must be selected. This time is usually set equal to EF of the last activity. In case of multiple finish activities, the activity with the largest EF is chosen as LF, however when an imposed project duration deadline exist that date will be used. In this example the LF is set to be equal to EF of activity E, which is 140 days. The LS for activity E is 90 days ''(LF –DUR = LS, 140 – 50 = 90)''. The late start for activity E becomes the LF for activity D, which is 90 days. By using the formula mentioned in this section LS can be calculated for all activities. Reaching to activity B it can be seen that it is a burst activity since it has more than one successor. The LF of activity B is controlled by the LS of activities C and F. According to rule no. 3 the smallest LS should be selected. LS of activity C is 20 days and LS of activity F is 30 days, therefore LS of activity C becomes LF of activity B. The latest activity B can finish is 20 days. Once the LS for activities A and B have been calculated the backward pass is completed and the latest activity time is known (A: 140 – 120 = 20, B: 20 – 20 = 0). The solution of the calculation can be seen in ''Figure 6''. | ||
[[File:Backward.png|1000px|thumb|center|Figure 6: Project network backward pass.]] | [[File:Backward.png|1000px|thumb|center|Figure 6: Project network backward pass.]] | ||
===Slack calculation=== | ===Slack calculation=== | ||
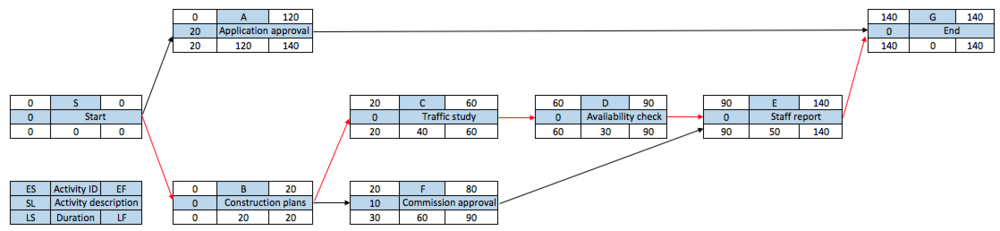
| − | After the computation of the forward and backward pass, it is possible to determine the slack (SL) for each activity. By computing the SL, it is possible to determine which activities can be delayed and how much without delaying the project. The total | + | After the computation of the forward and backward pass, it is possible to determine the ''slack (SL)'' for each activity. By computing the SL, it is possible to determine which activities can be delayed and how much without delaying the project. The total SL is the difference between the LS and the ES '''(LS – ES = SL)''' and between the LF and EF '''(LF – EF = SL)'''. For example, in ''Figure 7'' the SL for activity F is ''30 – 20 = 10'' days. This means that activity F can be delayed by 10 days without delaying the whole project. If the SL of one activity is used, the ES for all activities that follow in the chain will be delayed and their slack reduced. |
| − | The critical path can be identified | + | The '''critical path''' can be identified after the computation of the SL for each activity. Activities that have ''zero slack'' belong to the critical path. As can be seen in ''Figure 7'', the activities on the critical path are '''B, C, D and E'''. Delay of any of these activities will delay the total project by the same number of days. |
[[File:Slack.png|1000px|thumb|center|Figure 7: Project network with slack and critical path.]] | [[File:Slack.png|1000px|thumb|center|Figure 7: Project network with slack and critical path.]] | ||
=Time-Cost Trade-Off= | =Time-Cost Trade-Off= | ||
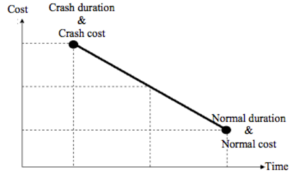
| − | [[File:crashgraph.png| | + | [[File:crashgraph.png|300px|thumb|right|Figure 8: The relationship between the duration of an activity and its direct cost.]] |
| − | The aim of ''' | + | The aim of '''The Time-Cost Trade-Off '''analysis is to reduce the original project duration, determined from the CPM, to meet a specific deadline, with the least cost. In general, there is a trade-off between the time and the direct cost to complete an activity, the less expensive the resource the larger duration they take to complete an activity. Shortening the duration on an activity will normally increase its direct cost. A simple version of the relationship between the duration of an activity and its direct cost can be seen in ''Figure 8''. The normal cost shown in the graph is the least direct cost required to complete an activity, and the corresponding duration is called the normal duration. The crash duration is the shortest duration required to complete the activity and the corresponding cost is called the crash cost.<ref name=TradeOff>Elbeltagi, E. (n.d.). ''Construction Management''. Pp. 164-174 about project time-cost trade-off. Retrieved September 12, 2016, from http://osp.mans.edu.eg/elbeltagi/CM%20CH8%20Time-Cost.pdf.</ref> |
| − | + | To solve the time-cost trade-off problem several heuristic approaches can be used, such as the cost slope method. A step by step procedure for that method is summarised as follow:<ref name=TradeOff/> | |
| − | To solve the time-cost trade-off problem several heuristic approaches can be used, such as the cost slope method. | + | |
#Apply the CPM technique as mentioned in the Application section to identify the critical path. | #Apply the CPM technique as mentioned in the Application section to identify the critical path. | ||
#Compute the cost slope for each activity by applying following equation: '''Cost slope = (crash cost – normal cost) / (normal duration – crash duration)'''. | #Compute the cost slope for each activity by applying following equation: '''Cost slope = (crash cost – normal cost) / (normal duration – crash duration)'''. | ||
| Line 161: | Line 166: | ||
#The cost increase is calculated by multiplying the cost slope with the shortening time of the activities. | #The cost increase is calculated by multiplying the cost slope with the shortening time of the activities. | ||
#This heuristic approach should be continued until no further shortening is possible and the crash point is reached. | #This heuristic approach should be continued until no further shortening is possible and the crash point is reached. | ||
| − | |||
| − | |||
| − | + | ===Example of the Time-Cost Trade-Off=== | |
| − | + | To get a deeper understanding of how the application of this method works a detailed example will be shown here below.<ref name=TradeOff/> | |
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | ||
| Line 229: | Line 232: | ||
|} | |} | ||
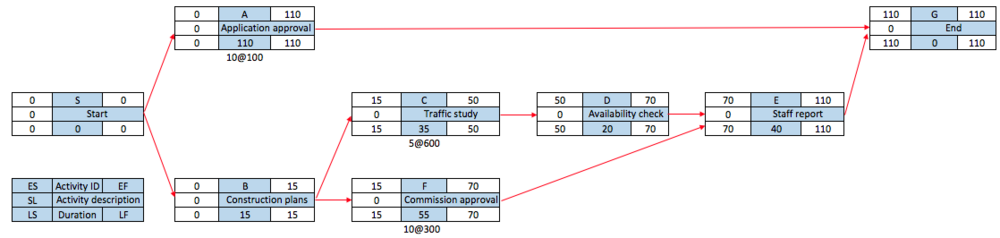
| − | The aim is to crash the project duration to 110 days. As mentioned in the Application section, the normal project duration is 140 days and the critical path is B-C-D-E. Project total normal cost is the sum the normal cost in Table 2, which is 48.300. | + | The aim is to crash the project duration to ''110 days''. As mentioned in the Application section, the normal project duration is 140 days and the critical path is B-C-D-E. Project total normal cost is the sum the normal cost in ''Table 2'', which is ''48.300''. |
| + | |||
[[File:Trade1.png|1000px|thumb|center|Figure 9: Project network including cost slope information.]] | [[File:Trade1.png|1000px|thumb|center|Figure 9: Project network including cost slope information.]] | ||
| − | The cost slope in Figure 9 is calculated by inserting relevant values into the cost slope equation. For example, for activity C the cost slope is (22 | + | The cost slope in ''Figure 9'' is calculated by inserting relevant values into the cost slope equation, ''(crash cost – normal cost) / (normal duration – crash duration)''. For example, for activity C the cost slope is ''(22.000-16.000) / (40-30) = 600''. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must then be adjusted. |
| − | [[File: | + | |
| + | [[File:Trade2a.png|1000px|thumb|center|Figure 10: Project network after activity D has been crashed.]] | ||
| − | Figure 10 shows the network after activity D has been crashed by 10 days. A new critical path is performed, B-F-E and the project duration is 130 days. Since activity D was crashed by 10 days and the crash cost is 60, | + | ''Figure 10'' shows the network after activity D has been crashed by 10 days. A new critical path is performed, '''B-F-E''', and the project duration is ''130 days''. Since activity D was crashed by 10 days and the crash cost is 60, the direct cost increases by ''10x60 = 600''. The project direct cost at this point is ''48.300+600 = 48.900''. |
| − | From | + | From ''Figure 10'' it can be seen that the activity on the critical path that has the lowest cost slope is activity E, which will be shortened by 10 days. The timing for activities that follow activity E must then be adjusted. |
[[File:Trade3.png|1000px|thumb|center|Figure 11: Project network after activity E has been crashed.]] | [[File:Trade3.png|1000px|thumb|center|Figure 11: Project network after activity E has been crashed.]] | ||
| − | Figure 11 shows the network after activity E has been crashed by 10 days. All activities are now critical and the project duration is 120 days. Since activity E was crashed by 10 days and the crash cost is 120, | + | ''Figure 11'' shows the network after activity E has been crashed by 10 days. All activities are now critical and the project duration is ''120 days''. Since activity E was crashed by 10 days and the crash cost is 120, the direct cost increases by ''10x120 = 1200''. The project direct cost at this point is ''48.900+1.200 = 50.100''. |
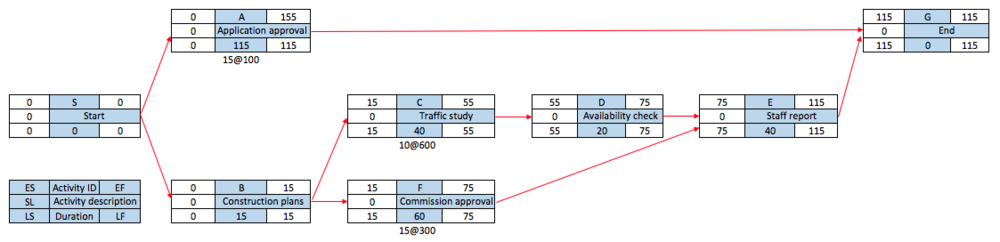
| − | From Figure 11 here above is can be seen that it is hard to decrease the duration on one activity to decrease the project’s duration. There are two options at this point, either to crash an activity on all critical paths or choose several activities on different paths to crash. Here is is relevant to crash activity A and B by 5 days since they have the lowest cost slope | + | From ''Figure 11'' here above is can be seen that it is hard to decrease the duration on one activity to decrease the project’s duration. There are two options at this point, either to crash an activity on all critical paths or choose several activities on different paths to crash. Here is is relevant to crash activity A and B by 5 days since they have the lowest cost slope. |
[[File:Trade4.png|1000px|thumb|center|Figure 12: Project network after activities A and B have been crashed.]] | [[File:Trade4.png|1000px|thumb|center|Figure 12: Project network after activities A and B have been crashed.]] | ||
| − | Figure 12 shows the network after activities A and B have been crashed by 5 days each. All activities are still critical and the project duration is 115 days. Since activities A and B were crashed by 5 days and the crash cost are 100 and 200, the direct cost increases by | + | ''Figure 12'' shows the network after activities A and B have been crashed by 5 days each. All activities are still critical and the project duration is ''115 days''. Since activities A and B were crashed by 5 days and the crash cost are 100 and 200, the direct cost increases by ''5x(100x200) = 1.500''. The project direct cost at this point is ''50.100+1.500 = 50.600''. |
| − | By looking at Figure 12 here above it can be seen that the next step is to decrease the duration of an activity from each path, activities A, C and F by 5 days. Since the reduction is 5 days and the crash cost is 100, 600 and 300, the direct cost increases by | + | By looking at ''Figure 12'' here above it can be seen that the next step is to decrease the duration of an activity from each path, activities A, C and F by 5 days. Since the reduction is 5 days and the crash cost is 100, 600 and 300, the direct cost increases by ''5x(100+600+300) = 5.000''. The project direct cost at this final stage is ''50.600+5.000 = 67.600'' and the project duration is ''110 days''. The new network diagram can be seen in ''Figure 13'' here below. |
[[File:Trade5.png|1000px|thumb|center|Figure 13: Project network after activities A, C and F have been crashed.]] | [[File:Trade5.png|1000px|thumb|center|Figure 13: Project network after activities A, C and F have been crashed.]] | ||
| Line 255: | Line 260: | ||
=Comparison to related project management techniques= | =Comparison to related project management techniques= | ||
| − | There are several project management techniques that are related to CPM, e.g. '''Project Management and Review Technique(PERT)''' and '''Critical Chain Method(CCM)'''. These methods are used for management of projects with the aim to finish on time and within budget. Nevertheless, there are many differences between all these methods which will be discussed in this section. | + | There are several project management techniques that are related to the CPM, e.g. '''Project Management and Review Technique(PERT)''' and '''Critical Chain Method(CCM)'''. These methods are used for management of projects with the aim to finish on time and within budget. Nevertheless, there are many differences between all these methods which will be discussed in this section. |
| − | '''CPM''' and '''PERT''' are often used in conjunction with each other to manage projects in a successful way. One of their differences is that PERT is a project management technique where planning, scheduling, organising, coordinating and controlling of uncertain activities is done, while CPM is a statistical technique of project management in which planning, scheduling, organising, coordination and control of well-defined activities | + | '''CPM''' and '''PERT''' are often used in conjunction with each other to manage projects in a successful way. One of their differences is that PERT is a project management technique where planning, scheduling, organising, coordinating and controlling of uncertain activities is done, while CPM is a statistical technique of project management in which planning, scheduling, organising, coordination and control of well-defined activities take place. Another difference is that PERT is a technique of planning and control of time while CPM is a method to control cost and time. Furthermore, the focus is on events when PERT is applied. Unlike CPM, where the focus is on activities. Lastly, to shorten project duration with least additional cost a cashing technique can be applied to CPM, however the crashing concept is not applicable to PERT. There are many more differences between these methods which will not be discussed further in this article. <ref>Surbni, S. (2015). ''Differences Between PERT and CPM''. Retrieved September 5, 2016, from http://keydifferences.com/difference-between-pert-and-cpm.html#Definition. </ref> |
| − | Moving on to the '''CCM''' which is built on '''CPM'''. Both methods are “Critical” and as their name suggest there are similarities and differences among the two of them. The main differences are that CPM involves the calculation of ES, EF, LS, LF and SL through forwards and backward passes in the project and focuses on the sequence of activities and the estimated duration of individual task in a straight forward manner. | + | Moving on to the '''CCM''' which is built on '''CPM'''. Both methods are “Critical” and as their name suggest there are similarities and differences among the two of them. The main differences are that CPM involves the calculation of ES, EF, LS, LF and SL through forwards and backward passes in the project and focuses on the sequence of activities and the estimated duration of individual task in a straight forward manner. While CPM add task buffers to each task, the CCM put tasks together in a chain by considering the minimal time needed for individual tasks. An overall project buffer is combined to the end of the project chain. <ref name=cpmVSccm>Chung, E. (2016). ''Critical Path Method vs Critical Chain Method for PMP Exam''. Retrieved September 5, 2016, from http://edward-designer.com/web/critical-path-method-vs-critical-chain-method-for-pmp-exam/. </ref> |
=Advantages and disadvantages/limitations of CPM= | =Advantages and disadvantages/limitations of CPM= | ||
| − | CPM tool has proved to be very valuable and beneficial when it comes to managing projects. Advantages of using this method are many and the list could get rather long. Listed here below are few of the advantages that organisations could gain by using CPM: <ref name=adv1>Anderson, E. B. & Hales, S. T. (1986). ''Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES)''. Pp. 1-2. Retrieved September 8, 2016, from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.115.6122&rep=rep1&type=pdf. </ref> <ref name=adv2> ''Advantages of Critical Path Method (CPM)''. Retrieved September 8, 2016, from http://theconstructor.org/construction/const-management/scheduling/advantages-of-critical-path-method-cpm/6873/. </ref> | + | The CPM tool has proved to be very valuable and beneficial when it comes to managing projects. Advantages of using this method are many and the list could get rather long. Listed here below are few of the advantages that organisations could gain by using CPM:<ref name=disadv1/> <ref name=adv1>Anderson, E. B. & Hales, S. T. (1986). ''Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES)''. Pp. 1-2. Retrieved September 8, 2016, from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.115.6122&rep=rep1&type=pdf. </ref> <ref name=adv2> ''Advantages of Critical Path Method (CPM)''. Retrieved September 8, 2016, from http://theconstructor.org/construction/const-management/scheduling/advantages-of-critical-path-method-cpm/6873/. </ref> |
| − | * | + | *CPM requires project members to graphically draw and identify various activities that need to be completed. This encourages the users to think through a project logically and critically and it helps preventing the chance of overlooking necessary activities and goals of a project. Furthermore, the project network diagram helps predicting the completion time of the project and can be a good assist in planning and scheduling the activities required for the completion of the project. |
| − | *CPM provides a realistic and disciplined method for determining how to attain the project objectives and for communicating and documenting the project plans, schedules, time and cost performance clearly and concisely in the scheduling stage, where a time chart is constructed for each activity. | + | *CPM provides a realistic and disciplined method for determining how to attain the project objectives and for communicating and documenting the project plans, schedules, time and cost performance clearly and concisely in the scheduling stage, where a time chart is constructed for each activity. |
| − | * | + | *CPM identifies the most critical elements in the plan making the managers focusing on the activities that are most constraining on the scheduling. It also determines the allocation of resources and prevents that the same resource is allocated for the same period of time. CPM will generate new schedules when there are changes in the durations of the activities and as technical or procedural changes are considered, CPM provides an easy method for evaluating the effects these changes have on the overall project schedule. |
| + | *It is possible to optimize the time-cost relationship by using the CPM as managers can visually identify the activities that can pose a problem if not managed and monitored effectively over a period of time. | ||
| + | *The CPM identifies the entire chain of activities, which makes it possible for the project managers to focus on the groups of activities that are immediate and have the ability to impact the next downstream activity. In additional, the CPM also identifies the slack in projects. Therefore, project managers can identify when resources can be reallocated to different activities to optimize the utilization of the resources. | ||
| + | *CPM can help managers identify suitable plan of actions to handle the multiple critical paths, as well as helping estimating the project duration which can be used to minimize the sum of direct and indirect costs involved in the project planning and scheduling. | ||
| − | Moving on the disadvantages and limitations of CPM. As for most of the management methods available, CPM faces several disadvantages and limitations, mainly as result of the technical and conceptual factors involved in the Critical Path Analysis(CPA) process. The below list include few of the advantages and limitations of CPM: <ref name=disadv1>Stealth, P. & Roy, G. L. (2009). ''Project’s Analysis through CPM (Critical Path Method)''. Pp. 23-25. Retrieved September 8, 2016, from http://www.iiuedu.eu/press/journals/sds/sds1_july_2008/05_SECC_01.pdf. </ref> <ref name=disadv2> ''Advantages and disadvantages in the implementation of CPM''. Retrieved September 8, 2016, from http://www.cpmscheduling.com/critical-path-method/advantages-and-disadvantages-in-the-implementation-of-cpm. </ref> <ref name=disadv3>Sinha, DK. (2015). ''Critical Path Method(CPM): Definition, Advantages and Limitations''. Retrieved September 8, 2016, from http://www.yourarticlelibrary.com/business/planning-business/critical-path-method-cpm-definition-advantages-and-limitations/40754/. </ref> | + | Moving on the disadvantages and limitations of CPM. As for most of the management methods available, CPM faces several disadvantages and limitations, mainly as result of the technical and conceptual factors involved in the Critical Path Analysis(CPA) process. The below list include few of the advantages and limitations of CPM:<ref name=disadv1>Stealth, P. & Roy, G. L. (2009). ''Project’s Analysis through CPM (Critical Path Method)''. Pp. 23-25. Retrieved September 8, 2016, from http://www.iiuedu.eu/press/journals/sds/sds1_july_2008/05_SECC_01.pdf. </ref> <ref name=disadv2> ''Advantages and disadvantages in the implementation of CPM''. Retrieved September 8, 2016, from http://www.cpmscheduling.com/critical-path-method/advantages-and-disadvantages-in-the-implementation-of-cpm. </ref> <ref name=disadv3>Sinha, DK. (2015). ''Critical Path Method(CPM): Definition, Advantages and Limitations''. Retrieved September 8, 2016, from http://www.yourarticlelibrary.com/business/planning-business/critical-path-method-cpm-definition-advantages-and-limitations/40754/. </ref> |
| − | *CPM can become extremely complicated and the complexity increases as the scope | + | *CPM can become extremely complicated and the complexity increases as the scope of big projects increase. The risk of making a mistake in the calculation of the critical path becomes very high. If projects are not well defined CPM can become ineffective and difficult to manage. |
| − | + | *It requires software to monitor the plan in bulky and lengthy projects. The set up and initial cost can be high, as well as the cost of maintaining the software. | |
| − | *It requires software to monitor the plan in bulky and lengthy projects. | + | |
*Critical path of a big project has to be calculated carefully since it is not always clear. In big projects CPM takes longer to identify and monitor the critical path. In many cases the critical paths might change and past critical paths may no longer be valid. This requires that the managers have to constantly review the network diagram and identify the changes occurred over the time. | *Critical path of a big project has to be calculated carefully since it is not always clear. In big projects CPM takes longer to identify and monitor the critical path. In many cases the critical paths might change and past critical paths may no longer be valid. This requires that the managers have to constantly review the network diagram and identify the changes occurred over the time. | ||
*CPM operates on the assumption that there is a precise known time that each activity in the project will take, but that is not always the case in real practice. | *CPM operates on the assumption that there is a precise known time that each activity in the project will take, but that is not always the case in real practice. | ||
| − | *The time | + | *It gets more complicated to understand the needs of the critical paths when there is more than one critical path in the project. In many cases, these paths are parallel and feed into a common node in the network diagram. In these situations it becomes difficult to identify the best utilization of technology and resources for the critical paths. |
| − | * | + | *The scheduling of workers changes as the critical paths and the slack change. It is often tricky to reallocate workers as the individual might be working on more than one project at a time and if the services of the individual are required on more than one critical path the identification and distribution of the labor time can cause overloading of the worker. |
| + | *It can often be difficult to identify the critical paths, especially if the project is unique. The traditional way of providing estimated time and cost depends on the historical data maintained by the company. When these data are not available, decision makers are forced to speculate and assume time and cost requirements for the projects. | ||
| − | = | + | =Annotated Bibliography= |
| − | + | ||
| − | + | ||
| − | < | + | '''Larson, E. W & Gray, C. F. (2011). Project Management, the managerial process. 5th edition.'''<ref name=PMbook /> |
| − | + | This book provides a holistic, integrative view of project management. It focuses on concept and skills that are used by managers to propose, plan, secure resources, and lead project teams to successful completions of their projects and helps understanding why organizations have developed a formal project management process to gain a competitive advantage. The concepts and techniques for managing projects in a successful way are discussed. The book can be used as a guide when dealing with typical problems that arise in project management. Pages 3-10 describe the definition of a project and the importance of Project Management. Pages 157-172 describe the development of a project plan and the construction of a project network. | |
| − | |||
| − | < | + | '''Stealth, P. & Roy, G. L. (2009). Project’s Analysis through CPM (Critical Path Method).'''<ref name=disadv1 /> |
| − | + | The focus of this study is to help the reader understand and evaluate the critical paths and critical chains in projects. It provides the reader with the policies and procedures to measure and monitor the critical paths. Furthermore, this study evaluates the similarities and differences in the concepts of the critical path and the critical chain. It investigates CPM and CCM methodologies in a generic format. | |
| − | = | + | |
| + | '''Anderson, E. B. & Hales, S. T. (1986). Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES).'''<ref name=adv1 /> | ||
| + | |||
| + | This report explains the Critical Path Method and describes the mathematical concepts behind it. The steps of how to construct a project network are explained as well as the resource analysis and cost analysis. Furthermore, it illustrates how a computerized CPM approach can be applied to a resource management or other research projects. | ||
| + | |||
| + | |||
| + | '''Elbeltagi, E. (n.d.). Construction Management. Pp. 164-174 about project time-cost trade-off'''.<ref name=TradeOff/> | ||
| + | |||
| + | This chapter explains the impact of time and cost trade-off in activities. It shows how this analysis is related to the critical path method and guides the reader towards the goal of reducing the original project duration, determined from the critical path analysis, with the least cost by determining the cost slope. Additionally, the study discusses the relationship between the time and cost. | ||
| + | |||
| + | =References= | ||
| + | <references /> | ||
Latest revision as of 12:44, 18 December 2018
Developed by Chalida Jaidee
Projects normally include many activities involving lots of different people. Due to this it can be difficult for project managers to have an overview of and keep track of things. In such situation The Critical Path Method (CPM) can be a useful tool. CPM is a step by step technique that is used to schedule a set of project activities. It analysis what activities are least flexible and the project duration is predicted based on the activities that fall along the critical path. The critical path is the longest sequence of activities in a project plan which must be completed on time in order for the project to complete on the predetermined scheduled date.[1] Delaying an activity on the critical path leads to a delay on the completion time of the entire project as these activities have no slack. Activities along the path cannot start until the predecessor activity is completed. When using CPM to plan a project a graphical diagram is often represented showing how each activity is related to the others.[2] This method is one of several tools that is important to keep projects on track and is convenient for all forms of projects, including research projects, product development, construction industry, maintenance and many more.
A joint venture between the Dupont chemical company and computer firm Remington Rand Univac led to a development of the Critical Path Method in the 1950's to tackle the interrelationships of separate activities within a project schedule.[3]
In this article the CPM is described, a step by step guidance on how to apply the method is discussed and the trade-off between cost and time is analysed. Furthermore, a comparison to other project management techniques is performed and its limitations and advantages are addressed. The main focus of this article is to walk the readers through the CPM process step by step with the aim that they will be able to execute the method after reading this article.
Contents |
[edit] Overview
[edit] Introduction and purpose of CPM

“A project is a temporary endeavor undertaken to create a unique product or service”.[5] The major goal of a project is to satisfy customer’s needs and achieve an organizations’s strategic plan. Projects are unique as they are different in some distinguishing way from all other projects. They have a life cycle were the life span is limited and there are predictable changes in level of effort and focus over the life of the projects. Project life cycle generally passes sequentially through four stages: defining, planning, executing and delivering. This is illustrated in Figure 1.[6]
To meet project requirements, it is important to have a good knowledge of project management. “If you fail to plan you are planning to fail” is a phrase often used. This can be related to project management, which is an application of knowledge, skills and a set of tools that improves the ability to plan, implement, and manage activities to accomplish specific organizational objectives. Not only is project management a set of tools, it is also a result-oriented management style that places a premium on building collaborative relationships among a diverse cast of characters. [6]
When managing projects, it is crucial to have a good understanding of the Triple constraint (also known as The Project Management Triangle). These constraints, time, scope and cost, form a triangle with a quality in the center as can be seen in Figure 2. They are all fully inter-related, which means that if one side is altered the other two will be affected in some manner. These constraints must be handled effectively for successful completion of any project as well as for the company to meet their customer quality requirements.[8] In order for this to be fulfilled the CPM technique can be a good assist.
[edit] History
A Dupont engineer, Morgan R. Walker and a Remington-Rand computer expert, James E. Kelly, Jr. developed the CPM in the 1950'. They created a unique way of representing the operations in the system, which involved using unique arrow filled diagrams. At the similar time, the U.S. Navy initiated a project called Program Evaluation Research Task (PERT). The purpose of that was to provide naval management with an effective manner by which they could periodically evaluate the information of the new Fleet Ballistic Missile program. With this the US Navy could obtain valid information of the project's progress and also have a reasonable accurate projection of the completion of the project as desired. It is worth mentioning that PERT does not include the quantity, quality and cost information, it only deals with the time constraints.[9] PERT-CPM was a successful tool for the hardware-oriented programs, but its application in resource management problems was limited. As CPM techniques were modified and designed to operate on the smaller new computer systems, they proved useful in smaller projects such as design and marketing of new products, maintenance and shutdown schedules, and research and development programs.[10]
Today, there are several project management softwares that can be chosen to execute the CPM in complex projects, such as Microsoft project. Despite that, it is important as a project manager to have an understanding of how to apply the CPM techniques by hand.
[edit] General methodology
CPM is an algorithm for scheduling a set of activities. It calculates the longest path of planned activities to logical end points or to the end of the project, as well as the earliest and latest that each activity can start and finish without increasing the project duration. This process determines which activities are critical (i.e. on the longest path) and which have slack (i.e. can be delayed without increasing the project duration). Critical path is a sequence of project network activities which ass up to the longest overall duration. It determines the shortest time possible to complete the project. Any delay of an activity on the critical path directly impacts the planned project completion date (i.e. there is no slack on the critical path). A project can have several, parallel, near critical paths. An additional parallel path through the network with the total durations shorter than the critical path is called a sub-critical or non-critical path. The sensitivity of the network increases with increasing number of critical paths.[11]
The essential technique for using CPM is to construct a model of the project that includes:
- A list of all activities required to complete the project (typically categorised within a work breakdown structure).
- The time (duration) that each activity will take to complete.
- The dependencies between the activities.
- Creation of the network diagram based on the activities, dependencies and durations.
- Logical end points such as milestones or deliverable items.
- Identification of the critical path with three steps:
- Forward pass procedure
- Backward pass procedure
- Slack computation
- Follow up and regular update of the network diagram when there is a change in the project.
[edit] Application
To get a deeper understanding of the application of CPM a detailed description will be presented step by step in this section with an example.
[edit] CPM node layout
The CPM network consist of CPM nodes for each and every activity. The number of the nodes in each network is dependent on the size of the project. The layout can be seen in Figure 3. To make the layout complete following informations must be filled out in the graph box:
- Activity ID: Each activity has a unique identification number.
- Activity description: Description of the activity.
- Duration: The time it takes to complete each activity.
- ES: Stands for early start. This is the earliest starting time of an activity.
- EF: Stands for early finish. This is the earliest finish time of an activity.
- LS: Stands for late start. This is the latest starting time of an activity.
- LF: Stands for late finish. This is the latest finish time of an activity.
- SL: Stands for slack. It represents how long and activity can be delayed without affecting the duration of the project.
[edit] CPM network creation
First step in the CPM process is to construct the CPM network, which is developed from the WBS. The network is a visual flow diagram of sequence, interrelationship, and dependencies of all the activities that must be accomplished to complete the project. The network is built using nodes and arrows, where the node represents an activity and the arrow shows dependency and project flow.[6]
Basic rules that apply in general when developing a project network are as follow:[6]
- Networks flow from left to right.
- All preceding connected activities must be completed before the following activity can begin.
- Arrows can cross over each other.
- Each activity should have a unique ID code.
- An activity identification number must be larger than any activities that precede it.
- Recycling through a set of activities cannot occur.
- Conditional statements are not allowed.
A CPM network diagram can be constructed given the following informations: A list of all activities involved in a project and their descriptions, a list of its precedences for each activity and lastly a list of the duration of each activity. Table 1 is an example of the list of activities that will be used to construct a CPM network diagram in this article.[6]
| Activity | Description | Preceding Activity | Duration [day] |
|---|---|---|---|
| |
Application approval | |
|
| |
Construction plans | |
|
| |
Traffic study | |
|
| |
Availability check | |
|
| |
Staff report | |
|
| |
Commission approval | |
|
By applying the basic rules mentioned here above a network can be constructed as can be seen in Figure 4. It shows the network with the activity time estimates found in the nodes. For example, activity A has an activity duration of 120 days, and activity C has an activity duration of 40 days. These informations are used in the next step called forward pass.
[edit] Forward pass
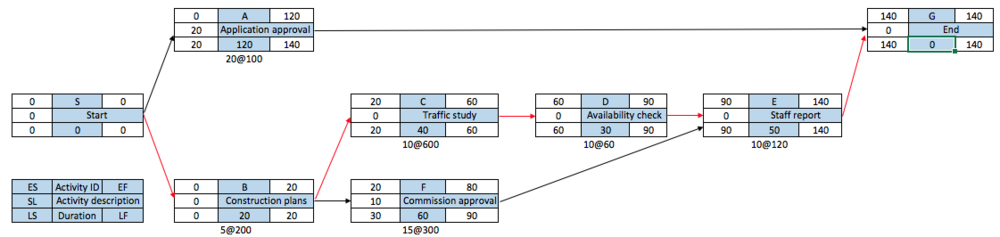
The second step is to calculate the ES, EF and expected normal completion time (TE) by using the forward pass computation. This process requires that each path is traced through the network to the last project activity. The longest path denotes the project completion time for the plan and is called the critical path. There are three steps that are important to keep in mind when using forward pass:[6]
- Activity times are added along each path in the network: ES + DUR = EF.
- The EF is carried to the next activity where it becomes its ES. However, there is one exception which is,
- If the next succeeding activity is a merge activity (activity that has more than one predecessor), the largest EF of all its immediate predecessor activities is selected.
The forward pass begins with the project early start time (ES), which is 0 in this example (activity A and B). This time is found in the upper left corner of the activity nodes in Figure 5. The early finish for activity A is 120 = 0+120 (ES + DUR = EF). The same formula is used to calculate EF for activity B, which resulted in 20 days. Next, it can be seen that activity B is the predecessor for activities C and F. Therefore, the earliest these activities can begin is when activity B is completed. Using the formula mentioned here above the EF can be calculated for all the activities. Reaching to activity E it can be seen that is is a merge activity since it has more than one predecessor. The ES of activity E is controlled by the EF of activities D and F. According to rule no. 3 the largest EF should be selected. Because activity D has higher EF than activity F it controls the ES of activity E, therefore ES for activity E is 90 days. The EF for activity E is 140 days, which is the earliest the project can be expected to complete(TE) under normal conditions. Now since ES, EF and TE is known the next step is to move to the backward pass process.
[edit] Backward pass
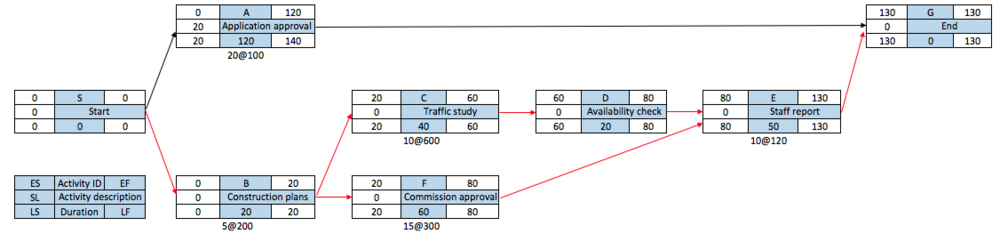
The third step, the backward pass is similar to the forward pass, except for it requires that the start point is from the last project activity(ies) and each path is traced backward to find LS and LF for each activity. There are three things that are important to keep in mind when using the backward pass process:[6]
- Activity times are subtracted along each path starting with the project end activity: LF – DUR = LS.
- LS is carried to the next preceding activity to establish its LF. However, there is one exception which is,
- If the next preceding activity is a burst activity (activity that has more than one successor), the smallest LS of all its immediate successor activities is selected to establish its LF.
Before the backward pass can be computed, LF for the last activity(ies) must be selected. This time is usually set equal to EF of the last activity. In case of multiple finish activities, the activity with the largest EF is chosen as LF, however when an imposed project duration deadline exist that date will be used. In this example the LF is set to be equal to EF of activity E, which is 140 days. The LS for activity E is 90 days (LF –DUR = LS, 140 – 50 = 90). The late start for activity E becomes the LF for activity D, which is 90 days. By using the formula mentioned in this section LS can be calculated for all activities. Reaching to activity B it can be seen that it is a burst activity since it has more than one successor. The LF of activity B is controlled by the LS of activities C and F. According to rule no. 3 the smallest LS should be selected. LS of activity C is 20 days and LS of activity F is 30 days, therefore LS of activity C becomes LF of activity B. The latest activity B can finish is 20 days. Once the LS for activities A and B have been calculated the backward pass is completed and the latest activity time is known (A: 140 – 120 = 20, B: 20 – 20 = 0). The solution of the calculation can be seen in Figure 6.
[edit] Slack calculation
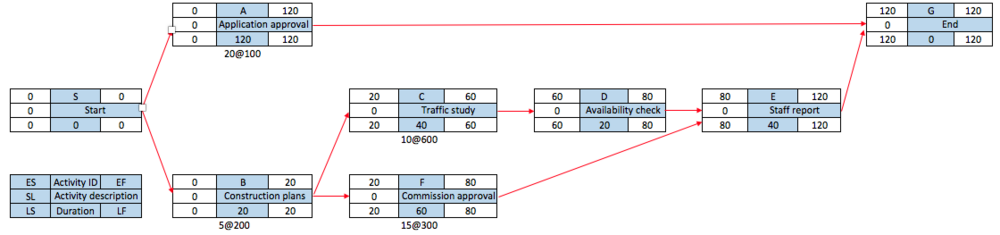
After the computation of the forward and backward pass, it is possible to determine the slack (SL) for each activity. By computing the SL, it is possible to determine which activities can be delayed and how much without delaying the project. The total SL is the difference between the LS and the ES (LS – ES = SL) and between the LF and EF (LF – EF = SL). For example, in Figure 7 the SL for activity F is 30 – 20 = 10 days. This means that activity F can be delayed by 10 days without delaying the whole project. If the SL of one activity is used, the ES for all activities that follow in the chain will be delayed and their slack reduced.
The critical path can be identified after the computation of the SL for each activity. Activities that have zero slack belong to the critical path. As can be seen in Figure 7, the activities on the critical path are B, C, D and E. Delay of any of these activities will delay the total project by the same number of days.
[edit] Time-Cost Trade-Off
The aim of The Time-Cost Trade-Off analysis is to reduce the original project duration, determined from the CPM, to meet a specific deadline, with the least cost. In general, there is a trade-off between the time and the direct cost to complete an activity, the less expensive the resource the larger duration they take to complete an activity. Shortening the duration on an activity will normally increase its direct cost. A simple version of the relationship between the duration of an activity and its direct cost can be seen in Figure 8. The normal cost shown in the graph is the least direct cost required to complete an activity, and the corresponding duration is called the normal duration. The crash duration is the shortest duration required to complete the activity and the corresponding cost is called the crash cost.[12]
To solve the time-cost trade-off problem several heuristic approaches can be used, such as the cost slope method. A step by step procedure for that method is summarised as follow:[12]
- Apply the CPM technique as mentioned in the Application section to identify the critical path.
- Compute the cost slope for each activity by applying following equation: Cost slope = (crash cost – normal cost) / (normal duration – crash duration).
- Shorten the activity duration on the critical path that has the least cost slope and has not been shortened to its crash duration.
- Keep reducing the duration of the activities on the critical path that have the lowest cost slope until its crash duration is reached or until the critical path changes.
- In some cases, multiple critical paths are involved. The activity(ies) to shorten is determined by comparing the cost slope of the activity on all critical paths with the sum of cost slope for a group of activities.
- Once a critical path is shortened the duration of the activities and the slack should be adjusted.
- The cost increase is calculated by multiplying the cost slope with the shortening time of the activities.
- This heuristic approach should be continued until no further shortening is possible and the crash point is reached.
[edit] Example of the Time-Cost Trade-Off
To get a deeper understanding of how the application of this method works a detailed example will be shown here below.[12]
| Activity | Description | Preceding Activity | Normal duration [day] | Normal cost | Crash duration [day] | Crash cost |
|---|---|---|---|---|---|---|
| |
Application approval | |
|
|
|
|
| |
Construction plans | |
|
|
|
|
| |
Traffic study | |
|
|
|
|
| |
Availability check | |
|
|
|
|
| |
Staff report | |
|
|
|
|
| |
Commission approval | |
|
|
|
|
The aim is to crash the project duration to 110 days. As mentioned in the Application section, the normal project duration is 140 days and the critical path is B-C-D-E. Project total normal cost is the sum the normal cost in Table 2, which is 48.300.
The cost slope in Figure 9 is calculated by inserting relevant values into the cost slope equation, (crash cost – normal cost) / (normal duration – crash duration). For example, for activity C the cost slope is (22.000-16.000) / (40-30) = 600. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must then be adjusted.
Figure 10 shows the network after activity D has been crashed by 10 days. A new critical path is performed, B-F-E, and the project duration is 130 days. Since activity D was crashed by 10 days and the crash cost is 60, the direct cost increases by 10x60 = 600. The project direct cost at this point is 48.300+600 = 48.900.
From Figure 10 it can be seen that the activity on the critical path that has the lowest cost slope is activity E, which will be shortened by 10 days. The timing for activities that follow activity E must then be adjusted.
Figure 11 shows the network after activity E has been crashed by 10 days. All activities are now critical and the project duration is 120 days. Since activity E was crashed by 10 days and the crash cost is 120, the direct cost increases by 10x120 = 1200. The project direct cost at this point is 48.900+1.200 = 50.100.
From Figure 11 here above is can be seen that it is hard to decrease the duration on one activity to decrease the project’s duration. There are two options at this point, either to crash an activity on all critical paths or choose several activities on different paths to crash. Here is is relevant to crash activity A and B by 5 days since they have the lowest cost slope.
Figure 12 shows the network after activities A and B have been crashed by 5 days each. All activities are still critical and the project duration is 115 days. Since activities A and B were crashed by 5 days and the crash cost are 100 and 200, the direct cost increases by 5x(100x200) = 1.500. The project direct cost at this point is 50.100+1.500 = 50.600.
By looking at Figure 12 here above it can be seen that the next step is to decrease the duration of an activity from each path, activities A, C and F by 5 days. Since the reduction is 5 days and the crash cost is 100, 600 and 300, the direct cost increases by 5x(100+600+300) = 5.000. The project direct cost at this final stage is 50.600+5.000 = 67.600 and the project duration is 110 days. The new network diagram can be seen in Figure 13 here below.
[edit]
There are several project management techniques that are related to the CPM, e.g. Project Management and Review Technique(PERT) and Critical Chain Method(CCM). These methods are used for management of projects with the aim to finish on time and within budget. Nevertheless, there are many differences between all these methods which will be discussed in this section.
CPM and PERT are often used in conjunction with each other to manage projects in a successful way. One of their differences is that PERT is a project management technique where planning, scheduling, organising, coordinating and controlling of uncertain activities is done, while CPM is a statistical technique of project management in which planning, scheduling, organising, coordination and control of well-defined activities take place. Another difference is that PERT is a technique of planning and control of time while CPM is a method to control cost and time. Furthermore, the focus is on events when PERT is applied. Unlike CPM, where the focus is on activities. Lastly, to shorten project duration with least additional cost a cashing technique can be applied to CPM, however the crashing concept is not applicable to PERT. There are many more differences between these methods which will not be discussed further in this article. [13]
Moving on to the CCM which is built on CPM. Both methods are “Critical” and as their name suggest there are similarities and differences among the two of them. The main differences are that CPM involves the calculation of ES, EF, LS, LF and SL through forwards and backward passes in the project and focuses on the sequence of activities and the estimated duration of individual task in a straight forward manner. While CPM add task buffers to each task, the CCM put tasks together in a chain by considering the minimal time needed for individual tasks. An overall project buffer is combined to the end of the project chain. [14]
[edit] Advantages and disadvantages/limitations of CPM
The CPM tool has proved to be very valuable and beneficial when it comes to managing projects. Advantages of using this method are many and the list could get rather long. Listed here below are few of the advantages that organisations could gain by using CPM:[9] [10] [15]
- CPM requires project members to graphically draw and identify various activities that need to be completed. This encourages the users to think through a project logically and critically and it helps preventing the chance of overlooking necessary activities and goals of a project. Furthermore, the project network diagram helps predicting the completion time of the project and can be a good assist in planning and scheduling the activities required for the completion of the project.
- CPM provides a realistic and disciplined method for determining how to attain the project objectives and for communicating and documenting the project plans, schedules, time and cost performance clearly and concisely in the scheduling stage, where a time chart is constructed for each activity.
- CPM identifies the most critical elements in the plan making the managers focusing on the activities that are most constraining on the scheduling. It also determines the allocation of resources and prevents that the same resource is allocated for the same period of time. CPM will generate new schedules when there are changes in the durations of the activities and as technical or procedural changes are considered, CPM provides an easy method for evaluating the effects these changes have on the overall project schedule.
- It is possible to optimize the time-cost relationship by using the CPM as managers can visually identify the activities that can pose a problem if not managed and monitored effectively over a period of time.
- The CPM identifies the entire chain of activities, which makes it possible for the project managers to focus on the groups of activities that are immediate and have the ability to impact the next downstream activity. In additional, the CPM also identifies the slack in projects. Therefore, project managers can identify when resources can be reallocated to different activities to optimize the utilization of the resources.
- CPM can help managers identify suitable plan of actions to handle the multiple critical paths, as well as helping estimating the project duration which can be used to minimize the sum of direct and indirect costs involved in the project planning and scheduling.
Moving on the disadvantages and limitations of CPM. As for most of the management methods available, CPM faces several disadvantages and limitations, mainly as result of the technical and conceptual factors involved in the Critical Path Analysis(CPA) process. The below list include few of the advantages and limitations of CPM:[9] [16] [17]
- CPM can become extremely complicated and the complexity increases as the scope of big projects increase. The risk of making a mistake in the calculation of the critical path becomes very high. If projects are not well defined CPM can become ineffective and difficult to manage.
- It requires software to monitor the plan in bulky and lengthy projects. The set up and initial cost can be high, as well as the cost of maintaining the software.
- Critical path of a big project has to be calculated carefully since it is not always clear. In big projects CPM takes longer to identify and monitor the critical path. In many cases the critical paths might change and past critical paths may no longer be valid. This requires that the managers have to constantly review the network diagram and identify the changes occurred over the time.
- CPM operates on the assumption that there is a precise known time that each activity in the project will take, but that is not always the case in real practice.
- It gets more complicated to understand the needs of the critical paths when there is more than one critical path in the project. In many cases, these paths are parallel and feed into a common node in the network diagram. In these situations it becomes difficult to identify the best utilization of technology and resources for the critical paths.
- The scheduling of workers changes as the critical paths and the slack change. It is often tricky to reallocate workers as the individual might be working on more than one project at a time and if the services of the individual are required on more than one critical path the identification and distribution of the labor time can cause overloading of the worker.
- It can often be difficult to identify the critical paths, especially if the project is unique. The traditional way of providing estimated time and cost depends on the historical data maintained by the company. When these data are not available, decision makers are forced to speculate and assume time and cost requirements for the projects.
[edit] Annotated Bibliography
Larson, E. W & Gray, C. F. (2011). Project Management, the managerial process. 5th edition.[6]
This book provides a holistic, integrative view of project management. It focuses on concept and skills that are used by managers to propose, plan, secure resources, and lead project teams to successful completions of their projects and helps understanding why organizations have developed a formal project management process to gain a competitive advantage. The concepts and techniques for managing projects in a successful way are discussed. The book can be used as a guide when dealing with typical problems that arise in project management. Pages 3-10 describe the definition of a project and the importance of Project Management. Pages 157-172 describe the development of a project plan and the construction of a project network.
Stealth, P. & Roy, G. L. (2009). Project’s Analysis through CPM (Critical Path Method).[9]
The focus of this study is to help the reader understand and evaluate the critical paths and critical chains in projects. It provides the reader with the policies and procedures to measure and monitor the critical paths. Furthermore, this study evaluates the similarities and differences in the concepts of the critical path and the critical chain. It investigates CPM and CCM methodologies in a generic format.
Anderson, E. B. & Hales, S. T. (1986). Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES).[10]
This report explains the Critical Path Method and describes the mathematical concepts behind it. The steps of how to construct a project network are explained as well as the resource analysis and cost analysis. Furthermore, it illustrates how a computerized CPM approach can be applied to a resource management or other research projects.
Elbeltagi, E. (n.d.). Construction Management. Pp. 164-174 about project time-cost trade-off.[12]
This chapter explains the impact of time and cost trade-off in activities. It shows how this analysis is related to the critical path method and guides the reader towards the goal of reducing the original project duration, determined from the critical path analysis, with the least cost by determining the cost slope. Additionally, the study discusses the relationship between the time and cost.
[edit] References
- ↑ BusinessDictionary. (2016). Critical Path. Retrieved September 8, 2016, from http://www.businessdictionary.com/definition/critical-path.html.
- ↑ Webodia. (2016). Critical Path Method. Retrieved September 8, 2016, from http://www.webopedia.com/TERM/C/Critical_Path_Method.html.
- ↑ Kielmas, M. (2016). History of the Critical Path Method. Retrieved September 8, 2016, from http://smallbusiness.chron.com/history-critical-path-method-55917.html.
- ↑ Francis, D., Horine, G. & Tittel, E. (2008). The Relationship Between Project Lifecycle and Project Management Processes. Retrieved September 8, 2016, from http://flylib.com/books/en/2.466.1.51/1/.
- ↑ Project Management Institute. (2000). A Guide to the Project Management Body of Knowledge. Pp. 4. Retrieved September 10, 2016, from http://www.cs.bilkent.edu.tr/~cagatay/cs413/PMBOK.pdf.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 Larson, E. W & Gray, C. F. (2011). Project Management, the managerial process. 5th edition, Pp. 3-10, 157-172. USA: NY. ISBN 978-0-07-340334-2.
- ↑ Haughey, D. (2011). Understanding the projoect management triple constraint. Retrieved September 16, 2016, from https://www.projectsmart.co.uk/understanding-the-project-management-triple-constraint.php.
- ↑ ProgramSucess. (2011). Scope, Time and Cost – Managing the Triple Constraint. Retrieved September 8, 2016, from https://programsuccess.wordpress.com/2011/05/02/scope-time-and-cost-managing-the-triple-constraint/.
- ↑ 9.0 9.1 9.2 9.3 Stealth, P. & Roy, G. L. (2009). Project’s Analysis through CPM (Critical Path Method). Pp. 23-25. Retrieved September 8, 2016, from http://www.iiuedu.eu/press/journals/sds/sds1_july_2008/05_SECC_01.pdf.
- ↑ 10.0 10.1 10.2 Anderson, E. B. & Hales, S. T. (1986). Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES). Pp. 1-2. Retrieved September 8, 2016, from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.115.6122&rep=rep1&type=pdf.
- ↑ Hansen, Z. N. L. (2016). Project planning. Retrieved from CampusNet in course 42459, planning and scheduling in manufacturing services.
- ↑ 12.0 12.1 12.2 12.3 Elbeltagi, E. (n.d.). Construction Management. Pp. 164-174 about project time-cost trade-off. Retrieved September 12, 2016, from http://osp.mans.edu.eg/elbeltagi/CM%20CH8%20Time-Cost.pdf.
- ↑ Surbni, S. (2015). Differences Between PERT and CPM. Retrieved September 5, 2016, from http://keydifferences.com/difference-between-pert-and-cpm.html#Definition.
- ↑ Chung, E. (2016). Critical Path Method vs Critical Chain Method for PMP Exam. Retrieved September 5, 2016, from http://edward-designer.com/web/critical-path-method-vs-critical-chain-method-for-pmp-exam/.
- ↑ Advantages of Critical Path Method (CPM). Retrieved September 8, 2016, from http://theconstructor.org/construction/const-management/scheduling/advantages-of-critical-path-method-cpm/6873/.
- ↑ Advantages and disadvantages in the implementation of CPM. Retrieved September 8, 2016, from http://www.cpmscheduling.com/critical-path-method/advantages-and-disadvantages-in-the-implementation-of-cpm.
- ↑ Sinha, DK. (2015). Critical Path Method(CPM): Definition, Advantages and Limitations. Retrieved September 8, 2016, from http://www.yourarticlelibrary.com/business/planning-business/critical-path-method-cpm-definition-advantages-and-limitations/40754/.