Impact and Probability in Risk Assessment
| (23 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| + | ''Developed by Karlotta Thorhallsdóttir'' | ||
| + | |||
| + | |||
'''Impact''' and '''probability''' are the two main components of [[Risk analysis]]. Looking at impact versus probability is common in order to categorize and prioritize risks as some risks may have a severe impact on projects objectives but only happen on rare occasions, while other have a moderate impact but occur more frequently. | '''Impact''' and '''probability''' are the two main components of [[Risk analysis]]. Looking at impact versus probability is common in order to categorize and prioritize risks as some risks may have a severe impact on projects objectives but only happen on rare occasions, while other have a moderate impact but occur more frequently. | ||
All organizations activities involve risk. Risks are events caused by uncertainties, which can have a positive or negative effect on the project objectives. All projects are unique and thus the associated risk varies between projects. Therefore, [[Risk Management]] is an important part of any organization as proper management increases the likelihood for the success of a project <ref name=" Winch " />. Risk management involves identifying possible risks and analyzing their potential in order to respond to and control the projects most significant threats and opportunities <ref name="Maylor"/>. | All organizations activities involve risk. Risks are events caused by uncertainties, which can have a positive or negative effect on the project objectives. All projects are unique and thus the associated risk varies between projects. Therefore, [[Risk Management]] is an important part of any organization as proper management increases the likelihood for the success of a project <ref name=" Winch " />. Risk management involves identifying possible risks and analyzing their potential in order to respond to and control the projects most significant threats and opportunities <ref name="Maylor"/>. | ||
| − | The risk analysis is a two-stage assessment process. Initially, qualitative methods are used to examine, categorize and determine the main risk events identified, which are relevant for a more detailed quantitative assessment. In risk analysis, risk is traditionally defined as a function of probability and impact <ref name=" Curtis " />. The probability is the likelihood of an event occurring and the consequences, to which extent the project is affected by an event, are the impacts of risk. By combining the probability and impact, the ''Level of Risk'' can be determined. There are various aspects of the project that can be affected by a risk event, such as cost, safety, operation, quality, etc <ref name=" Curtis " />. A commonly used method for risk assessment is preparing descriptive scales to rank risk in terms of probability and impact. These are often referred to as ''Impact and Probability Matrix'' and can take both qualitative and numerical values. The Impact and Probability Matrix is a simple and easily understood method of prioritizing risks and allocating resources. There are other, quantitative methods for analyzing risks, such as ''Sensitivity analysis'', ''Expected Monetary Value'' analysis and ''Monte Carlo Simulations''. All these methods, though beneficial for management, have their limitations and drawbacks <ref name="MITRE"/>. | + | The risk analysis is a two-stage assessment process. Initially, qualitative methods are used to examine, categorize and determine the main risk events identified, which are relevant for a more detailed quantitative assessment. In risk analysis, risk is traditionally defined as a function of probability and impact <ref name=" Curtis " />. The probability is the likelihood of an event occurring and the consequences, to which extent the project is affected by an event, are the impacts of risk. By combining the probability and impact, the ''Level of Risk'' can be determined. There are various aspects of the project that can be affected by a risk event, such as cost, safety, operation, quality, etc <ref name=" Curtis " />. A commonly used method for risk assessment is preparing descriptive scales to rank risk in terms of probability and impact. These are often referred to as ''Impact and Probability Matrix'' and can take both qualitative and numerical values. The Impact and Probability Matrix is a simple and easily understood method of prioritizing risks and allocating resources. There are other, quantitative methods for analyzing risks, such as ''Sensitivity analysis'', ''Expected Monetary Value'' ''analysis'' and ''Monte Carlo Simulations''. All these methods, though beneficial for management, have their limitations and drawbacks <ref name="MITRE"/>. |
| Line 95: | Line 98: | ||
== Qualitative Analysis== | == Qualitative Analysis== | ||
| − | Qualitative methods for risk assessment are relatively rapid in practice, cost effective and easily understood <ref name=" Curtis " />. The results | + | Qualitative methods for risk assessment are relatively rapid in practice, cost effective and easily understood <ref name=" Curtis " />. The results from the qualitative assessments are not an accurate estimate of risk. However, they provide a rather descriptive result and often with sufficient information for planning responses. The results from these assessments also set the foundation for more detailed quantitative analysis, if possible and warranted. It is performed regularly throughout a projects life cycle as new risks may emerge at later stages as well as a risk response may result in other risk events <ref name=" PMI " />. Classifying the risks enables organizations to reduce uncertainty levels and focus primarily on the high-risk events. There are two qualitative methods of assessing risk events in terms of impact and probability, both involving rating the impact and probability. These are ''Risk Probability and Impact Assessment'' and ''Probability and Impact matrix'' <ref name=" PMI " />. |
=== Risk Probability and Impact Assessment === | === Risk Probability and Impact Assessment === | ||
| − | The probability assessment involves | + | The probability assessment involves estimating the likelihood of a risk occurring. The impact assessment estimates the effects of a risk event on a project objective. These impacts can be both positive and negative; i.e., opportunities and threats. The project objectives are numerous, e.g. the schedule, cost, quality and scope. For each identified risk, the impact and probability are assessed. Interviews and meeting with experienced project participants, stakeholders, and experts in the subject are the basis for the impact and probability assessment. These impacts and probabilities are rated and their level assessed. The risks which receive high ratings are investigated further or an appropriate response is planned. The low rated risks do not require an immediate action, but should be included in the [[Risk register]] for monitoring <ref name=" PMI " />. |
=== Probability and Impact Matrix === | === Probability and Impact Matrix === | ||
| − | The Probability and Impact Matrix is one the most commonly used qualitative assessment method. It is based on the two components of risk, probability of occurrence and the impact on objective | + | The Probability and Impact Matrix is one the most commonly used qualitative assessment method. It is based on the two components of risk, probability of occurrence and the impact on objective(s) if it occurs. The matrix is a two-dimensional grid that maps the likelihood of the risks occurrence and their effect on the project objectives <ref name=" PMI " />. The risk score, often referred to as ''risk level'' or the degree of risk, is calculated by multiplying the two axes of the matrix. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">Risk = Impact x Probability </div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">Risk = Impact x Probability </div> | ||
| − | As the impact and probability can be described in both a relative and numerical manner so can the risk score. The higher the combined ratings are, the higher the score and thus risk level. These ratings are generally defined from low to high or very low to very high <ref name=" Curtis " />. The ratings for likelihood and impact are made using gathered opinions from interviews <ref name="Maylor"/>. These ratings | + | As the impact and probability can be described in both a relative and numerical manner so can the risk score. The higher the combined ratings are, the higher the score and thus the risk level. These ratings are generally defined from low to high or from very low to very high <ref name=" Curtis " />. The ratings for likelihood and impact are made using gathered opinions from interviews <ref name="Maylor"/>. These ratings must be classified by each organization, specific for each activity. The organizations must define their risk tolerance. Creating these definitions of impact and probability levels can help reducing the influence of bias <ref name=" PMI " />. The result from these risk matrices are used to prioritize the risks, plan the risk response, identify risks for quantitative assessment and guide resource allocations <ref name="Cox" />. However, the objective effected by the risk must also be considered. E.g., a risk events which has high safety or health risk would be prioritized over a risk event which would have very high financial risk <ref name=" Curtis " />. |
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" | ||
| Line 151: | Line 154: | ||
|- | |- | ||
!style="height:20px; width:110px; text-align:center; background:#F2F2F2; " |Impact | !style="height:20px; width:110px; text-align:center; background:#F2F2F2; " |Impact | ||
| − | !style="height:20px; width: | + | !style="height:20px; width:100px; text-align:center; background:#F2F2F2; " |Very Low / 0.05 |
| − | !style="height:20px; width: | + | !style="height:20px; width:90px; text-align:center; background:#F2F2F2; " |Low / 0.1 |
| − | !style="height:20px; width: | + | !style="height:20px; width:90px; text-align:center; background:#F2F2F2; " |Moderate / 0.2 |
| − | !style="height:20px; width: | + | !style="height:20px; width:90px; text-align:center; background:#F2F2F2; " |High / 0.4 |
| − | !style="height:20px; width: | + | !style="height:20px; width:90px; text-align:center; background:#F2F2F2; " |Very High / 0.8 |
|- | |- | ||
|colspan= "6" style="height:10px; background: white; border color: white" | | |colspan= "6" style="height:10px; background: white; border color: white" | | ||
|- | |- | ||
|colspan = "1" style="height:15px; text-align:center; background: red; " | High risk | | |colspan = "1" style="height:15px; text-align:center; background: red; " | High risk | | ||
| − | |colspan = "2" style="height:15px; text-align:center; " | Score > 0. | + | |colspan = "2" style="height:15px; text-align:center; " | Score > 0.14 |
| − | |rowspan = "3" colspan = "3" ; text-align:left | A organization defines its risk thresholds, low, moderate and high. These thresholds | + | |rowspan = "3" colspan = "3" style="width:150px; text-align:left; " | A organization defines its risk thresholds, low, moderate and high. These thresholds can differ between projects. |
|- | |- | ||
|colspan = "1" style="height:15px; text-align:center; background: yellow; " | Moderate risk | |colspan = "1" style="height:15px; text-align:center; background: yellow; " | Moderate risk | ||
| − | |colspan = "2" style="height:20px; text-align:center; " | 0.05 < Score < 0. | + | |colspan = "2" style="height:20px; text-align:center; " | 0.05 < Score < 0.14 |
|- | |- | ||
|colspan = "1" style="height:15px; text-align:center; background: green; " | Low risk | |colspan = "1" style="height:15px; text-align:center; background: green; " | Low risk | ||
| Line 171: | Line 174: | ||
| − | [[File:winch PIM.JPG|400px|thumb|right|Risk Impacts and Probability Matrix, <ref name=" Winch" />]] | + | [[File:winch PIM.JPG|400px|thumb|right|Figure 1: Risk Impacts and Probability Matrix, <ref name=" Winch" />]] |
'''Low impact – Low probability:''' The risks that are characterized as low, or very low, risks have both a low impact and likelihood of occurrence. For negative risks, threats, the response required is not necessarily as proactive management action. However, they should be included within the risk register for future monitoring. Positive risks, opportunities, within the low-risk category should be monitored or just simply accepted. Opportunity acceptance means taking advantage of the opportunity if it arises, but not actively pursuing it <ref name=" PMI " />. | '''Low impact – Low probability:''' The risks that are characterized as low, or very low, risks have both a low impact and likelihood of occurrence. For negative risks, threats, the response required is not necessarily as proactive management action. However, they should be included within the risk register for future monitoring. Positive risks, opportunities, within the low-risk category should be monitored or just simply accepted. Opportunity acceptance means taking advantage of the opportunity if it arises, but not actively pursuing it <ref name=" PMI " />. | ||
| Line 183: | Line 186: | ||
== Quantitative Analysis == | == Quantitative Analysis == | ||
| − | Quantitative assessment methods provide | + | Quantitative assessment methods provide more accurate analysis results than the qualitative assessment. However, they are costlier and often time consuming, so only the risk prioritized by the qualitative assessment are analyzed. These methods are mostly used to analyze the combined effects of all affecting risks. The most important benefit is that the information produced support decision-making, and reduce project uncertainty. In some cases, quantitative methods are not applicable due to lack of sufficient data, but that must be evaluated by the project manager. The analysis should be repeated as a part of risk control to determine whether the overall risks are reaching a desirable state. There various methods for quantitative analysis; e.g. ''Sensitivity analysis'', ''Expected Monetary Value'' ''analysis'' and ''Monte Carlo Simulations'' <ref name=" PMI " />. |
=== Sensitivity Analysis === | === Sensitivity Analysis === | ||
| − | Sensitivity analysis is a quantitative technique useful to determine the variables which have the greatest effect on the risk <ref name="NRC" />. They help estimating risks with the most potential impact and how variations in the objectives and different uncertainties are correlated | + | Sensitivity analysis is a quantitative technique useful to determine the variables which have the greatest effect on the risk <ref name="NRC" />. They help estimating the risks with the most potential impact and how variations in the objectives and different uncertainties are correlated and the effect of each element on the objectives <ref name=" PMI " />. They also help assess probability of the project decisions, being affected by the risk actions, which results in the desired outcome. Generally, it is only the highest risk scenarios which are considered in the sensitivity analysis. These analyses can be time consuming and costly, this is often why qualitative analysis such as ''Probability and Impact Matrix'' is used to identify the highest concerning risks <ref name="SA" />. |
=== Expected Monetary Value Analysis === | === Expected Monetary Value Analysis === | ||
[[File:EMV.JPG|500px|thumb|right|Figure 2: Decision Tree diagram for EMV, <ref name=" PMI" /> (click for a clearer picture)]] | [[File:EMV.JPG|500px|thumb|right|Figure 2: Decision Tree diagram for EMV, <ref name=" PMI" /> (click for a clearer picture)]] | ||
| − | The main concept of Expected Monetary Value (EMV) is similar to the Impact and Probability Matrix as it involves multiplying the probability and impact. The probability of a risks occurring determined and the impact given a monetary value. Opportunities are typically expressed as positive values and the threats as negative. The EMV analysis calculates the average outcome of a future event, which may or may not occur. Decision Trees are often used to calculate the EMV <ref name=" PMI" />. | + | The main concept of Expected Monetary Value (EMV) is similar to the ''Impact and Probability Matrix'' as it involves multiplying the probability and impact. The probability of a risks occurring is determined and the impact given a monetary value. Opportunities are typically expressed as positive values and the threats as negative. The EMV analysis calculates the average outcome of a future event, which may or may not occur. Decision Trees are often used to calculate the EMV <ref name=" PMI" />. |
| − | Figure 2 shows an example of Decision Tree Diagram being used for EMV analysis. For a power plant in need of renovation, two | + | Figure 2 shows an example of a ''Decision Tree Diagram'' being used for EMV analysis. For a power plant in need of renovation, two actions are possible; to build a new plant or to upgrade the current one. The uncertainty that needs to be considered is the magnitude of the power demand. Stronger demand yields higher benefits but both outcomes result in higher benefits for the new power plant individually. For each action, there are two outcomes, the uncertainties, that need to be considered. The total benefits/losses are the difference between the invested costs and the revenue. There is a 40% probability of weak power demand and a 60% probability of strong power demand. By multiplying the probability with outcome benefits, and summing them up, gives the Expected Monetary Value of the actions. The action which offers the highest benefit is then chosen. When using ''Decision Tree diagrams''; the tree is drawn from right to left, considering all possible outcomes from the available data; and then adding the appropriate numbers from left to right <ref name=" PMI" />. EMV analysis is highly dependent on accurate, risk-neutral assumptions. The outcome of the EMV is used to plan and prioritize possible risk responses. |
[[File: MCS.JPG|300px|thumb|right|Figure 3: The respective probability of achieving specific cost targets, <ref name=" PMI" /> (click for a clearer picture)]] | [[File: MCS.JPG|300px|thumb|right|Figure 3: The respective probability of achieving specific cost targets, <ref name=" PMI" /> (click for a clearer picture)]] | ||
| + | |||
=== Monte Carlo Simulation === | === Monte Carlo Simulation === | ||
| − | Monte Carlo Simulations | + | Monte Carlo Simulations (MCS) are typically used for project simulations to quantify risks <ref name=" PMI" />. These random simulations can be considered as “experiments” and give insight into the likelihood of each outcome, the impact <ref name="NRC" />. In risk management, the inputs into the simulation are estimates of project objectives; e.g. cost of the project or schedule duration <ref name="Maylor"/>. A probability distribution is created for these variables, and a project model iterated many times with randomly chosen inputs using random number generators. The model outputs are the probability of each outcome due to the specific uncertainties. These outputs can then be used to plan the response. When performing MCS there are some things that need to be considered for the validity of the outcomes. Variables may not be independent, number of iterations may not be sufficient as more iterations are costlier and time consuming. Figure 3 shows the outcome of a MCS, analyzing the cost estimation of a project. There is only a 12% probability of meeting the budget of $41M. If an organization wants 75% probability of success, the budget would need to be $50M. |
= Limitations = | = Limitations = | ||
| − | Qualitative methods are imprecise. They are just estimates and it can happen that unlikely | + | Qualitative methods are imprecise. They are just estimates and it can happen that the unlikely risks occur and the likely risks sometimes never come to pass. The quality of the information available influences the quality of the results, therefore the information must be evaluated to help determine the risks importance <ref name=" Curtis " />. When using the ''Probability and Impact Matrix'', risk that are quantitatively different can get the same rating, and often the risks are overestimated. The results from the ''Probability and Impact Matrix'' are subjective and are thus open to more than one interpretation <ref name="Cox" />. The matrix doesn’t provide the possibility of assessing the overall project risks, nor does it address the risks interactions and correlations. Not all concepts of risks can be mapped to a ''Probability and Impact Matrix'', as the tool is designed around an event oriented risk concept. The practice often is impractical until a certain maturity level, where some of the best opportunities for risk management may have passed <ref name="PIM" />. |
| − | Quantitative methods often provide more accurate results but are costly and time consuming. Using numbers may imply more precision in results than there is. The data and techniques used in these methods also need to be considered. If the models used are incorrect or don’t represent reality the result is meaningless. | + | Quantitative methods often provide more accurate results but are costly and time consuming. Using numbers may imply more precision in results than there is. The data and techniques used in these methods also need to be considered. If the models used are incorrect or don’t represent reality, the result is meaningless. The same applies to the inputs. If the inputs are wrong the result from the analysis are useless. In risk analysis, this is a problem as assumptions are not always apparent <ref name=" Curtis " />. |
| Line 211: | Line 215: | ||
'''Winch, G.M. (2010) ''Managing Construction Projects: An Information Processing Approach, Second Edition.'' Oxford: Wiley-Blackwell Publishing. | '''Winch, G.M. (2010) ''Managing Construction Projects: An Information Processing Approach, Second Edition.'' Oxford: Wiley-Blackwell Publishing. | ||
| + | |||
''' | ''' | ||
| − | The book contains a description of the practice of managing risk and uncertainty in a construction project. It describes briefly the four activities of risk management process. The definitions of risk and uncertainty is described and the importance of risk management supported. Winch describes briefly the purpose of risk analysis and defines Probability and Impact matrix as the most commonly used tool for categorizing risks. The planned responses to risks that have been prioritized and categorized are also described within the same matrix as the probability and impact. | + | The book contains a description of the practice of managing risk and uncertainty in a construction project. It describes briefly the four activities of risk management process. The definitions of risk and uncertainty is described and the importance of risk management supported. Winch describes briefly the purpose of risk analysis and defines Probability and Impact matrix as the most commonly used tool for categorizing risks. The planned responses to risks that have been prioritized and categorized are also described within the same matrix as the probability and impact. |
| + | |||
'''Curtis, P. & Carey, M. (2012). ''Risk Assessment in Practice.'' Deloitte & Touche LLP.''' | '''Curtis, P. & Carey, M. (2012). ''Risk Assessment in Practice.'' Deloitte & Touche LLP.''' | ||
| + | |||
Risk Assessment in Practice is a framework developed by five private sector organizations with the goal of thought leadership. It focuses on risk assessment process and criteria, impact and probability and the practice of qualitative and quantitative methods for the assessment, categorization and prioritization of risk. The limitations and advantages of the methods are also discussed. | Risk Assessment in Practice is a framework developed by five private sector organizations with the goal of thought leadership. It focuses on risk assessment process and criteria, impact and probability and the practice of qualitative and quantitative methods for the assessment, categorization and prioritization of risk. The limitations and advantages of the methods are also discussed. | ||
| Line 234: | Line 241: | ||
<ref name="Cox"> Cox, L. (2008). What's Wrong with Risk Matrices? Risk analysis: an official publication of the Society for Risk Analysis. 28(2), 497-512 </ref> | <ref name="Cox"> Cox, L. (2008). What's Wrong with Risk Matrices? Risk analysis: an official publication of the Society for Risk Analysis. 28(2), 497-512 </ref> | ||
<ref name="SA"> Iloiu, M. & Csiminga, D. (2009). Project RISK Evaluation Methods - Sensitivity Analysis. Annals of the University of Petroşani, Economics, 9(2), 33-38 </ref> | <ref name="SA"> Iloiu, M. & Csiminga, D. (2009). Project RISK Evaluation Methods - Sensitivity Analysis. Annals of the University of Petroşani, Economics, 9(2), 33-38 </ref> | ||
| − | <ref name="PIM"> Risk Management Capability Ltd. (2005). | + | <ref name="PIM"> Risk Management Capability Ltd. (2005). Probability- Impact Matrix (PIM). http://www.rmcapability.com/resources/Capability+Guidance+Sheet+-+Probability-Impact+Matrix.pdf </ref> |
</references> | </references> | ||
| + | |||
| + | [[Category:Project Management]][[Category:Uncertaity]][[Category:Risk]][[Category:Risk Management]] | ||
Latest revision as of 14:57, 16 November 2018
Developed by Karlotta Thorhallsdóttir
Impact and probability are the two main components of Risk analysis. Looking at impact versus probability is common in order to categorize and prioritize risks as some risks may have a severe impact on projects objectives but only happen on rare occasions, while other have a moderate impact but occur more frequently.
All organizations activities involve risk. Risks are events caused by uncertainties, which can have a positive or negative effect on the project objectives. All projects are unique and thus the associated risk varies between projects. Therefore, Risk Management is an important part of any organization as proper management increases the likelihood for the success of a project [1]. Risk management involves identifying possible risks and analyzing their potential in order to respond to and control the projects most significant threats and opportunities [2]. The risk analysis is a two-stage assessment process. Initially, qualitative methods are used to examine, categorize and determine the main risk events identified, which are relevant for a more detailed quantitative assessment. In risk analysis, risk is traditionally defined as a function of probability and impact [3]. The probability is the likelihood of an event occurring and the consequences, to which extent the project is affected by an event, are the impacts of risk. By combining the probability and impact, the Level of Risk can be determined. There are various aspects of the project that can be affected by a risk event, such as cost, safety, operation, quality, etc [3]. A commonly used method for risk assessment is preparing descriptive scales to rank risk in terms of probability and impact. These are often referred to as Impact and Probability Matrix and can take both qualitative and numerical values. The Impact and Probability Matrix is a simple and easily understood method of prioritizing risks and allocating resources. There are other, quantitative methods for analyzing risks, such as Sensitivity analysis, Expected Monetary Value analysis and Monte Carlo Simulations. All these methods, though beneficial for management, have their limitations and drawbacks [4].
Contents |
[edit] Background
Risk management is a four-stage process. The first being identification of risks, second analysis (assessment), then the risk response and finally the risk monitoring [1]. In risk analysis, risk can be defined as a function of impact and probability [3]. In the analysis stage, the risks identified during the Risk Identification Process can be prioritized from the determined probability and impact of the risk event, using qualitative or quantitative methods. Other factors, such as the response time-frame and the tolerance should be taken into account when analyzing and categorizing the risks [5].
| Objective | Relative / Numerical Scale | |||||
|---|---|---|---|---|---|---|
| Very Low / 0.05 | Low / 0.1 | Moderate / 0.2 | High / 0.4 | Very High /0.8 | ||
| Cost | Insignificant change in cost | < 10% increase | 10 - 20% increase | 20 - 40% increase | > 40% increase | |
| Time | Insignificant change in schedule | < 5% increase | 5 - 10% increase | 10 - 20% increase | > 20% increase | |
| Scope | Barely noticeable scope decrease | Minor areas affected | Major areas affected | Unacceptable reduction | Project end item effectively useless | |
| Quality | Barely noticeable quality degradation | Only demanding applications effected | Quality reduction requires sponsor approval | Unacceptable quality reduction | Project end item effectively useless | |
[edit] Impact
Impacts are often defined as the consequences, or effects of a risk event on the project objectives. These impacts can be both beneficial or harmful to the objectives [3]. The impact of risk events on different project objectives can be defined in both a qualitative and quantitative manner. These project objectives are cost, schedule, quality, scope, health, safety, etc.
The Impact scale can vary, but the most common scale is the five-point scale. Typically, the impacts are described relatively; as very low, low, moderate, high and very high, but often also defined using numerical scales. Dependent on the objective, the scales are given a description of what the impact entails [5]. One risk event can affect more than one objective, so the impact of all the possible objectives effected must be considered [3]. Table 1 shows how the impact can be defined for various objectives. The possible impacts on each objective is described and given a ranking. The ranking in table 1 is both relative, from very low to very high, and numerical, giving numerical values based on the specific project.
| Likelihood | Description | |
|---|---|---|
| Relative | Numerical | |
| Very Low | 0.1 | Highly unlikely to occur. |
| Low | 0.3 | Will most likely not occur |
| Moderate | 0.5 | Possible to occur |
| High | 0.7 | Likely to occur |
| Very High | 0.9 | Highly likely to occur |
[edit] Probability
Risk probability, or likelihood, is the possibility of a risk event occurring. The likelihood can be expressed in both a qualitative and quantitative manner. When discussing probability in a qualitative manner, terms such as frequent, possible, rare etc. are used. It is also possible to describe the probability in a numerical manner. This can be done using scores, percentages and frequencies defined by the organizations dependent on the relative description [3]. Table 2 show an example on how an organization can define the ranking for the likelihood of risks. The table shows the ranking in both a relative and numerical manner and a description of the ranking is given.
[edit] Risk Assessment Methods Using Impact and Probability
Risk analysis is a two-stage process, with qualitative assessment being the first stage. By using qualitative methods for risk assessment, the risk can be categorized for further quantitative assessment or even risk response planning. Quantitative assessment is the next stage in risk analysis. The process involves analyzing the effects of risks on the overall project objectives. They primarily focus on the risks which have been prioritized in the qualitative assessment. To ensure the quality and credibility of the analysis, general definitions of impact and probability levels must be fitted to individual project context [5].
[edit] Qualitative Analysis
Qualitative methods for risk assessment are relatively rapid in practice, cost effective and easily understood [3]. The results from the qualitative assessments are not an accurate estimate of risk. However, they provide a rather descriptive result and often with sufficient information for planning responses. The results from these assessments also set the foundation for more detailed quantitative analysis, if possible and warranted. It is performed regularly throughout a projects life cycle as new risks may emerge at later stages as well as a risk response may result in other risk events [5]. Classifying the risks enables organizations to reduce uncertainty levels and focus primarily on the high-risk events. There are two qualitative methods of assessing risk events in terms of impact and probability, both involving rating the impact and probability. These are Risk Probability and Impact Assessment and Probability and Impact matrix [5].
[edit] Risk Probability and Impact Assessment
The probability assessment involves estimating the likelihood of a risk occurring. The impact assessment estimates the effects of a risk event on a project objective. These impacts can be both positive and negative; i.e., opportunities and threats. The project objectives are numerous, e.g. the schedule, cost, quality and scope. For each identified risk, the impact and probability are assessed. Interviews and meeting with experienced project participants, stakeholders, and experts in the subject are the basis for the impact and probability assessment. These impacts and probabilities are rated and their level assessed. The risks which receive high ratings are investigated further or an appropriate response is planned. The low rated risks do not require an immediate action, but should be included in the Risk register for monitoring [5].
[edit] Probability and Impact Matrix
The Probability and Impact Matrix is one the most commonly used qualitative assessment method. It is based on the two components of risk, probability of occurrence and the impact on objective(s) if it occurs. The matrix is a two-dimensional grid that maps the likelihood of the risks occurrence and their effect on the project objectives [5]. The risk score, often referred to as risk level or the degree of risk, is calculated by multiplying the two axes of the matrix.
As the impact and probability can be described in both a relative and numerical manner so can the risk score. The higher the combined ratings are, the higher the score and thus the risk level. These ratings are generally defined from low to high or from very low to very high [3]. The ratings for likelihood and impact are made using gathered opinions from interviews [2]. These ratings must be classified by each organization, specific for each activity. The organizations must define their risk tolerance. Creating these definitions of impact and probability levels can help reducing the influence of bias [5]. The result from these risk matrices are used to prioritize the risks, plan the risk response, identify risks for quantitative assessment and guide resource allocations [6]. However, the objective effected by the risk must also be considered. E.g., a risk events which has high safety or health risk would be prioritized over a risk event which would have very high financial risk [3].
| Probability | Threats | ||||
|---|---|---|---|---|---|
| Very High / 0.9 | 0.05 | 0.09 | 0.18 | 0.36 | 0.72 |
| High / 0.7 | 0.04 | 0.07 | 0.14 | 0.28 | 0.56 |
| Moderate / 0.5 | 0.03 | 0.05 | 0.10 | 0.20 | 0.40 |
| Low / 0.3 | 0.02 | 0.03 | 0.06 | 0.12 | 0.24 |
| Very Low / 0.1 | 0.01 | 0.01 | 0.02 | 0.04 | 0.08 |
| Impact | Very Low / 0.05 | Low / 0.1 | Moderate / 0.2 | High / 0.4 | Very High / 0.8 |
| High risk | | Score > 0.14 | A organization defines its risk thresholds, low, moderate and high. These thresholds can differ between projects. | |||
| Moderate risk | 0.05 < Score < 0.14 | ||||
| Low risk | Score < 0.05 | ||||
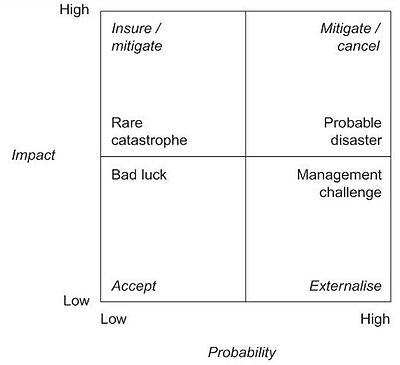
Low impact – Low probability: The risks that are characterized as low, or very low, risks have both a low impact and likelihood of occurrence. For negative risks, threats, the response required is not necessarily as proactive management action. However, they should be included within the risk register for future monitoring. Positive risks, opportunities, within the low-risk category should be monitored or just simply accepted. Opportunity acceptance means taking advantage of the opportunity if it arises, but not actively pursuing it [5].
High impact – Low probability: Risks with high impact but low likelihood of occurrence can be characterized from low to high risks but most often within the moderate category. The characterization is dependent on the organizations defined threshold. These events rarely occur, defined as rare catastrophes. It is difficult to determine the probability based on historical records due to lack of data. Therefore, the probabilities must be estimated subjectively. The most commonly responses are to insure or mitigate the problem [7].
Low impact – High probability: Risks with low impact but high likelihood of occurrence can be characterized from low to high risks but most often within the moderate category. The characterization is dependent on the organizations defined threshold. These risks are mostly due to uncertainties of numerous elements that individually, are minor risks but combined, could amount to higher risks. These are such uncertainties as actual cost and duration of different aspects of a project, changes to activates or other similar uncertainties, that alone, have little impact [7].
High impact – High probability: The risks that are characterized as high risks have both a high impact and likelihood of occurrence. A risk which has a negative impact, is a threat to the objective, may need priority actions and aggressive responses. These aggressive responses could be mitigation of the risk or even terminating the project if the risk is to great. A risk that has a positive impact, is an opportunity, is most likely obtained easily, with the greatest benefits and should thus be targeted first [5].
[edit] Quantitative Analysis
Quantitative assessment methods provide more accurate analysis results than the qualitative assessment. However, they are costlier and often time consuming, so only the risk prioritized by the qualitative assessment are analyzed. These methods are mostly used to analyze the combined effects of all affecting risks. The most important benefit is that the information produced support decision-making, and reduce project uncertainty. In some cases, quantitative methods are not applicable due to lack of sufficient data, but that must be evaluated by the project manager. The analysis should be repeated as a part of risk control to determine whether the overall risks are reaching a desirable state. There various methods for quantitative analysis; e.g. Sensitivity analysis, Expected Monetary Value analysis and Monte Carlo Simulations [5].
[edit] Sensitivity Analysis
Sensitivity analysis is a quantitative technique useful to determine the variables which have the greatest effect on the risk [7]. They help estimating the risks with the most potential impact and how variations in the objectives and different uncertainties are correlated and the effect of each element on the objectives [5]. They also help assess probability of the project decisions, being affected by the risk actions, which results in the desired outcome. Generally, it is only the highest risk scenarios which are considered in the sensitivity analysis. These analyses can be time consuming and costly, this is often why qualitative analysis such as Probability and Impact Matrix is used to identify the highest concerning risks [8].
[edit] Expected Monetary Value Analysis
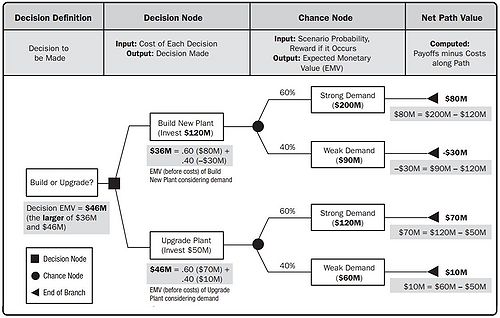
The main concept of Expected Monetary Value (EMV) is similar to the Impact and Probability Matrix as it involves multiplying the probability and impact. The probability of a risks occurring is determined and the impact given a monetary value. Opportunities are typically expressed as positive values and the threats as negative. The EMV analysis calculates the average outcome of a future event, which may or may not occur. Decision Trees are often used to calculate the EMV [5].
Figure 2 shows an example of a Decision Tree Diagram being used for EMV analysis. For a power plant in need of renovation, two actions are possible; to build a new plant or to upgrade the current one. The uncertainty that needs to be considered is the magnitude of the power demand. Stronger demand yields higher benefits but both outcomes result in higher benefits for the new power plant individually. For each action, there are two outcomes, the uncertainties, that need to be considered. The total benefits/losses are the difference between the invested costs and the revenue. There is a 40% probability of weak power demand and a 60% probability of strong power demand. By multiplying the probability with outcome benefits, and summing them up, gives the Expected Monetary Value of the actions. The action which offers the highest benefit is then chosen. When using Decision Tree diagrams; the tree is drawn from right to left, considering all possible outcomes from the available data; and then adding the appropriate numbers from left to right [5]. EMV analysis is highly dependent on accurate, risk-neutral assumptions. The outcome of the EMV is used to plan and prioritize possible risk responses.
[edit] Monte Carlo Simulation
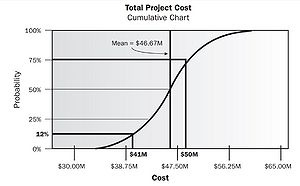
Monte Carlo Simulations (MCS) are typically used for project simulations to quantify risks [5]. These random simulations can be considered as “experiments” and give insight into the likelihood of each outcome, the impact [7]. In risk management, the inputs into the simulation are estimates of project objectives; e.g. cost of the project or schedule duration [2]. A probability distribution is created for these variables, and a project model iterated many times with randomly chosen inputs using random number generators. The model outputs are the probability of each outcome due to the specific uncertainties. These outputs can then be used to plan the response. When performing MCS there are some things that need to be considered for the validity of the outcomes. Variables may not be independent, number of iterations may not be sufficient as more iterations are costlier and time consuming. Figure 3 shows the outcome of a MCS, analyzing the cost estimation of a project. There is only a 12% probability of meeting the budget of $41M. If an organization wants 75% probability of success, the budget would need to be $50M.
[edit] Limitations
Qualitative methods are imprecise. They are just estimates and it can happen that the unlikely risks occur and the likely risks sometimes never come to pass. The quality of the information available influences the quality of the results, therefore the information must be evaluated to help determine the risks importance [3]. When using the Probability and Impact Matrix, risk that are quantitatively different can get the same rating, and often the risks are overestimated. The results from the Probability and Impact Matrix are subjective and are thus open to more than one interpretation [6]. The matrix doesn’t provide the possibility of assessing the overall project risks, nor does it address the risks interactions and correlations. Not all concepts of risks can be mapped to a Probability and Impact Matrix, as the tool is designed around an event oriented risk concept. The practice often is impractical until a certain maturity level, where some of the best opportunities for risk management may have passed [9]. Quantitative methods often provide more accurate results but are costly and time consuming. Using numbers may imply more precision in results than there is. The data and techniques used in these methods also need to be considered. If the models used are incorrect or don’t represent reality, the result is meaningless. The same applies to the inputs. If the inputs are wrong the result from the analysis are useless. In risk analysis, this is a problem as assumptions are not always apparent [3].
[edit] Annotated bibliography
Winch, G.M. (2010) Managing Construction Projects: An Information Processing Approach, Second Edition. Oxford: Wiley-Blackwell Publishing.
The book contains a description of the practice of managing risk and uncertainty in a construction project. It describes briefly the four activities of risk management process. The definitions of risk and uncertainty is described and the importance of risk management supported. Winch describes briefly the purpose of risk analysis and defines Probability and Impact matrix as the most commonly used tool for categorizing risks. The planned responses to risks that have been prioritized and categorized are also described within the same matrix as the probability and impact.
Curtis, P. & Carey, M. (2012). Risk Assessment in Practice. Deloitte & Touche LLP.
Risk Assessment in Practice is a framework developed by five private sector organizations with the goal of thought leadership. It focuses on risk assessment process and criteria, impact and probability and the practice of qualitative and quantitative methods for the assessment, categorization and prioritization of risk. The limitations and advantages of the methods are also discussed.
Project Management Institute, Inc. (2013). A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Fifth Edition. Newtown Square, Pennsylvania :Project Management Institute, Inc.
The Project Management Institute’s “A Guide to the Project Management Body of Knowledge” is a guideline for managing individual projects and defines project management related concepts as well as the life-cycle and processes of projects and project management. It defines nine knowledge areas and risk management is one of them. Risk analysis is one of the steps of risk management. The guidline describes various qualitative and quantitative methods for risk analysis, among them are the Impact and Probability Assessment, Impact and Probability Matrix and Sensitivity Analysis.
[edit] References
- ↑ 1.0 1.1 1.2 Winch, G.M. (2010) Managing Construction Projects: An Information Processing Approach, Second Edition. Oxford: Wiley-Blackwell Publishing
- ↑ 2.0 2.1 2.2 Maylor, H. (2010) Project Management, Fourth Edition. Harlow, England: Pearson Education Limited
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 Curtis, P. & Carey, M. (2012) Risk Assessment in Practice. Deloitte & Touche LLP
- ↑ The MITRE Corporation. (2014) MITRE Systems Engineering Guide. The United States: MITRE Corporate Communications and Public Affairs
- ↑ 5.00 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 5.11 5.12 5.13 5.14 5.15 5.16 5.17 5.18 Project Management Institute, Inc. (2013). A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Fifth Edition. Newtown Square, Pennsylvania: Project Management Institute, Inc
- ↑ 6.0 6.1 Cox, L. (2008). What's Wrong with Risk Matrices? Risk analysis: an official publication of the Society for Risk Analysis. 28(2), 497-512
- ↑ 7.0 7.1 7.2 7.3 National Research Council. (2005). The Owner’s Role in Project Risk Management. Washington, D.C: The National Academies Press
- ↑ Iloiu, M. & Csiminga, D. (2009). Project RISK Evaluation Methods - Sensitivity Analysis. Annals of the University of Petroşani, Economics, 9(2), 33-38
- ↑ Risk Management Capability Ltd. (2005). Probability- Impact Matrix (PIM). http://www.rmcapability.com/resources/Capability+Guidance+Sheet+-+Probability-Impact+Matrix.pdf