Reference class forecasting
(→Root causes of poor performance) |
(→Abstract) |
||
| (145 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
==Abstract == | ==Abstract == | ||
| − | The definition of project success according to the standard published by the project management institute is meeting customers' expectations without exceeding the desired requirement such as cost, duration, and scope. <ref name="PMBOK"> "Project Management Institute (PMI),2017, Guide to the Project Management Body of Knowledge (PMBOK® Guide) (6th Edition)" </ref> However, executing projects on time | + | The definition of project success according to the standard published by the project management institute is meeting customers' expectations without exceeding the desired requirement such as cost, duration, and scope.<ref name="PMBOK"> "Project Management Institute (PMI),2017, Guide to the Project Management Body of Knowledge (PMBOK® Guide) (6th Edition)" </ref> However, executing projects on time and within the estimated budget is a challenging aspect of project management. |
| + | On that matter, a research was conducted by the Danish professor Bent Flyvbjerg to study the reasons for cost and time overrun in megaprojects. Flyvbjerg proposed the so-called Reference Class Forecasting to overcome these challenges. Reference class forecasting (RCF) is a method that studies the overall view of a certain project by forecasting similar projects rather than focusing solely on the considered project. <ref name="Flyvbjerg 2005"/> This method assists managers to make decisions under uncertainties by assessing the risk of the planned project. <ref name="PMBOK"/> In this article, the root causes of the managerial problem will be presented based on statistical studies on project failures in terms of budget and time of completion, after highlighting the need for improvement in this particular. The big idea which is the RCF technique and its three-step approach will be presented. That will be followed by a case study to get a better understanding of the RCF application. Lastly, the problem of using the RCF method will be presented. | ||
== Root causes of poor performance == | == Root causes of poor performance == | ||
Research made on a sample of 258 large projects executed over the last 7 decades shows that 90% of these projects exceeded the original budget. According to re-searcher, almost all projects do not deliver the intended promises such as on-time completion and staying within budget. <ref name="Flyvbjerg2004"> "Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews https://doi.org/10.1080/0144164032000080494a"</ref>. The poor performance of a project is correlated to the managerial level such as project implementation and management methodology. <ref name=" Chemical Industry"/> Project failures are usually covered up and overlooked. However, Flyvbjerg has identified two explanatory models for the poor performance of a project. <ref name=" Flyvbjerg 2013"/> These models are: | Research made on a sample of 258 large projects executed over the last 7 decades shows that 90% of these projects exceeded the original budget. According to re-searcher, almost all projects do not deliver the intended promises such as on-time completion and staying within budget. <ref name="Flyvbjerg2004"> "Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews https://doi.org/10.1080/0144164032000080494a"</ref>. The poor performance of a project is correlated to the managerial level such as project implementation and management methodology. <ref name=" Chemical Industry"/> Project failures are usually covered up and overlooked. However, Flyvbjerg has identified two explanatory models for the poor performance of a project. <ref name=" Flyvbjerg 2013"/> These models are: | ||
| + | ====Optimism bias==== | ||
| + | This model accounts for the benefit shortfalls that are caused by planning fallacy and optimism bias. Optimism bias is a term coined by Daniel Kahnemann means that people tend to see the world in a more positive light. Flyvbjerg states that managers make decisions based on optimism and planning fallacy rather than rational gain and statistical probabilities due to overconfidence. That leads to underestimating cost, completion times, and risks of planned actions. These biases are most likely generated by focusing on the so-called "inside view" and considering the project at hand as one of a kind. Thus, planners who pursue initiative will most likely end up overrunning the estimated budget and duration <ref name=" Flyvbjerg 2013"/> | ||
| + | Anchoring and adjustment cause also biases of judgment. In the context of planning, the first estimate acts as a benchmark for a later stage estimate. That results in making adjustments that are not compatible with the reality of the project performance. | ||
| + | ====Strategic misrepresentation==== | ||
| + | This model accounts for unreliable planning and decision-making due to political pressure. When estimating the outcome of a project, planners tend consciously to overestimate the benefits and underestimate the cost to increase the likelihood of getting their projector plan approved. <ref name=" Flyvbjerg 2005"/> Thus, when political and organizational pressure are high, planners or project managers non-intentionally tend to underestimate the project cost and overestimate the benefits. However, to gain approval or funding, they intentionally use the following formula: <ref name=" Flyvbjerg 2013"/> | ||
| + | Project approval = Underestimated cost + Overestimated benefits <ref name=" Flyvbjerg 2013"/> | ||
| − | + | Poor performance can also be caused due to a technical error. For instance, unsuitable forecasting techniques, inadequate data, poor contract, etc. <ref name="Flyvbjerg 2005"/> However, this aspect of poor performance is beyond the scope of this article. | |
| − | + | == Big idea == | |
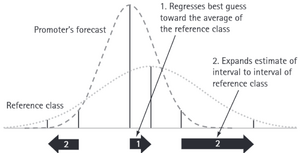
| − | + | [[File:RCFM.png|300px|thumb|right|Figure 1, What reference class forecasting does, in statisticians' language.<ref name= "Flyvbjerg 2013"/>]] | |
| + | Project managers should eliminate cognitive biases and reduce inaccuracy when making decisions, one method that is being used in infrastructure projects is Reference Class Forecasting. <ref name=" Chemical Industry" >"Walczak, R. and Majchrzak, T., 2018. Implementation of the Reference Class Forecasting Method for Projects Implemented in a Chemical Industry Company. Acta Oeconomica Pragensia. https://www.researchgate.net/publication/324337008_Implementation_of_the_Reference_Class_Forecasting_Method_for_Projects_Implemented_in_a_Chemical_Industry_Company" </ref> In this section, the RCF model will be explained followed by the three-steps implementation | ||
| + | ===Reference Class Forecasting=== | ||
| + | The reference class forecast provided an external point of view and act as an enabler of better planning based on historical data of projects that have similar attributes. By doing so, the project managers can reduce biases that are caused due to assessing available information "inside views" and neglecting unknown unknowns or other considerations "outside views".<ref name="Flyvbjerg 2005"/> RCFM is recommended by the American Planning Association which “encourages planners to use reference class forecasting in addition to traditional methods as a way to improve accuracy“. <ref name="Flyvbjerg 2005">" Flyvbjerg, B., 2007. Policy and planning for large-infrastructure projects: problems, causes, cures. Environment and Planning B: planning and design. http://documents1.worldbank.org/curated/en/968761468141298118/pdf/wps3781.pdf"</ref> This method of enhancing decision-making in light of un-certainties has proved to be effective. It allows for adjustments to be made in the original cost-benefit analysis (CBA) so the plan includes margin errors. <ref name="sciencedirect hydroelectric"> "Awojobi, O. and Jenkins, G.P., 2016. Managing the cost overrun risks of hydroelectric dams: An application of reference class forecasting techniques. Renewable and Sustainable Energy Reviews. https://www.sciencedirect.com/science/article/pii/S1364032116301162/" </ref> | ||
| + | This method attempts to fit a certain event into a probability of distribution of comparable class reference. However, from a statistical perspective, the reference class means prediction higher than the ordinary forecast estimate as it can see in figure 1. Also, the reference class prediction spreads the estimate of the conventional forecast interval. The reference class distribution is indicated by the dotted curve while the project promoters’ forecast, indicated by the dashed curve. <ref name="Flyvbjerg 2013"/> | ||
| + | === Three steps approach === | ||
| + | RCFM requires a large amount of work and should be implemented before initiating a project in order to get a unique opportunity on reflecting on the budget and planned duration. Implementing the RCFM requires a three-step approach, these steps are shown in figure 1 and explained thoroughly in the text below. | ||
| + | * Identify a reference class that has similar attributes to the project on hand. There is no role of thumbs when choosing a reference class. However, the reference class can not be narrow to get a reliable result if the categories were too small. The reference class can not be too wide either. Furthermore, the organization must also decide whether they want to create reference classes based on their projects within the programs or do they want to include reference classes from other organizations. <ref name="De-risking">"Pindy Bhullar, 2018, De-risking the programme portfolio with reference class forecasting. https://www.apm.org.uk/news/de-risking-the-programme-portfolio-with-reference-class-forecasting/"</ref> | ||
| + | * Determine a probability of distribution for the chosen reference classes. This requires trustful historical data from several projects within the reference class. The result of the probability distribution of the historical data will be used to estimate the level of uncertainty. From a statistical perspective, regression models are an essential tool in deriving the probability distribution. The empirical data is then utilized to establish the required optimism bias uplift. The uplift corresponds to the acceptable risk of cost and time overrun. <ref name="Flyvbjerg 2005"/> | ||
| + | * Comparing the project on hand with the reference class distribution in order to determine the desired outcome such as budget and project duration.<ref name="Flyvbjerg 2005"/> | ||
| − | + | == Application== | |
| + | In this section, a practical application of the reference class forecasting method in planning large dams will be illustrated briefly. The analysis is based on a data set constructed from the world Bank and consists of 58 dam projects located in 33 developing countries and constructed between 1976-2005. The case study conducted to derive an outside view of cost uncertainty for three major development regions -Africa, Asia, and Latin America. The study follows the three RCF steps approaches in addition to a further innovatory step of fitting multivariate multilevel models to the reference data in order to predict future cost and time of completion. The reason for fitting regression models to the historical data is to enable the managers to focus on specific project-level risk instead of risk in a reference class. Consequently, project managers can base their decisions on empirical data rather than their own judgments and optimism. The study aims to generate three different probability distributions covering each of the three development regions. <ref name="sciencedirect hydroelectric"/> However, this technique can be generalized and applied to different large-scale projects. Therefore, this section will highlight the framework, which is illustrated in figure 2, and avoid a detailed explanation of the case study result. | ||
| − | = | + | [[File:Implementation of RCF 1.png|750px|thumb|center|The framework was re-created by me but inspired by the case study researchers <ref name="sciencedirect hydroelectric"/>]] |
| − | |||
| − | == | + | === Step 1: Inputs === |
| − | + | The project is initiated by analyzing the level of cost and time overrun in the completed projects, then a simple univariate analysis is conducted to classify the relationship between cost and time performance and project characteristics. In the dams example, they identified the project cost as follows: Cost = f (site- geology, size, time, price-inputs) where the site- geology has been identified as a significant variable that causes a direct impact on the cost overrun.<ref name="sciencedirect hydroelectric"/> | |
| − | + | === Step 2: Output === | |
| + | The relationship between different projects can vary greatly across major groups. However, to capture the random effects in the dataset and to estimate the relationship between the different factors, hierarchical linear model HLM regression will be used. The regression model estimates the correlation between projects across sub-groups. For example, the causes of exceeding the budget in several projects in one country will most likely be similar. The cost and time of completion are then investigated using simple statistic tests and by fitting a multilevel regression model. The multi-level regression model allows correlation between estimate error within each sub-group. For instance, if the data set contains several projects from the same county, there is a high chance that the error of estimation will be similar across these projects. <ref name="sciencedirect hydroelectric"/> | ||
| − | + | The result of the regression will be used to derive the probability distribution function. Considering the case of the dams, the forecast errors were distributed as the table below shows. | |
| + | {| class="wikitable" style="text-align: center; color: blue;" | ||
| + | |colspan="1"| | ||
| + | |colspan="2"|Africa | ||
| + | |colspan="2"| Latin | ||
| + | |colspan="2" |Asia | ||
| + | |- | ||
| + | |- | ||
| + | |- | ||
| + | |Margine of forecast error | ||
| + | |Frequency | ||
| + | |Rel Frequency | ||
| + | |Frequency | ||
| + | |Rel Frequency | ||
| + | |Frequency | ||
| + | |Rel Frequency | ||
| + | |- | ||
| + | |More than 10% | ||
| + | |9 | ||
| + | |69% | ||
| + | |12 | ||
| + | |80% | ||
| + | |17 | ||
| + | |77% | ||
| + | |- | ||
| + | |More than 20% | ||
| + | |7 | ||
| + | |54% | ||
| + | |12 | ||
| + | |80% | ||
| + | |11 | ||
| + | |50% | ||
| + | |- | ||
| + | |More than 50% | ||
| + | |2 | ||
| + | |15% | ||
| + | |7 | ||
| + | |47% | ||
| + | |1 | ||
| + | |4% | ||
| + | |} | ||
| − | * | + | To summarize the result of all projects combined |
| − | + | * 79% of the projects constructed have an error in cost projection more than 10% | |
| − | + | * 62% of the projects constructed have an error in cost projection more than 20% | |
| + | * 19% of the projects constructed have an error in cost projection more than 50% | ||
| + | |||
| + | === Step 3: Decision === | ||
| + | [[File:uplift.png|300px|thumb|right|The acceptable level of risk in the dams constructed in Africa <ref name="sciencedirect hydroelectric"/> ]] | ||
| + | From the conducted analysis, we can conclude that there is misestimation in the project's cost. However, in this phase, the RCF method is used to improve the quality of decisions on dams. To do so, the level of uplift required will be determined based on the probability distribution of cost overrun. The acceptable level of risk in the dams constructed in Africa is shown in figure 3, the figure illustrates that, if the project manager wants to the tolerance for the decision as a 10% deviation of the actual cost then a 47% uplift will be required. The table below shows the required uplift for the three reference class according to several acceptable levels of risk tolerance. <ref name="sciencedirect hydroelectric"/> | ||
| + | |||
| + | {| class="wikitable" style="text-align: center; color: blue;" | ||
| + | |Refernce class | ||
| + | |Level of tolerance for risk | ||
| + | |Uplift | ||
| + | |- | ||
| + | |Africa | ||
| + | |10% | ||
| + | |47% | ||
| + | |- | ||
| + | |Latin America | ||
| + | |10% | ||
| + | |117% | ||
| + | |- | ||
| + | |Asia | ||
| + | |10% | ||
| + | |54% | ||
| + | |} | ||
| + | Lastly, to correct the estimate about the budget, the level of uplift required should be determined in order to eliminate the biases in cost and time estimates <ref name="sciencedirect hydroelectric"/> | ||
==Limitation == | ==Limitation == | ||
| − | RCF is not a new tool within the decision-making framework for mega infrastructure projects. However, its application to other fields is rare due to the lack of data on relevant reference classes or faulty information. | + | RCF is not a new tool within the decision-making framework for mega infrastructure projects. However, its application to other fields is rare due to the lack of data on relevant reference classes or faulty information. <ref name="sciencedirect hydroelectric"/> Alan Hájek has categorized the problem of RCF in probability theory into frequentism, classical, logical, propensity, subjectivism. These problems are stated and explained from a statistical point of view. However, frequentism and subjectivism are still relevant to explain briefly in this article. <ref name="problem "/> |
| + | === Frequentism=== | ||
| + | Probabilistic frequentism defines the probability of an event as the limit of its relative frequency. Since each event has an unlimited number of properties and attributes, then the event will be classified into an endless number of classes. To forecast the outcome of future events, first, we should find a suitable reference class. However, the forecasted event can be incorporated in several reference classes and each of them has its own probabilities. This problem grows bigger when the probabilities of these classes differ greatly from one another. <ref name="problem "/> | ||
| − | Last but not least, the RCF method is more convenient in cases where errors are due to non-random events such as human bias in decision making while uncertainty is present. | + | === Subjectivism === |
| + | The accuracy of the result generated by applying the RCF depends greatly on the sample size of the reference classes and the relevance of the reference class. Thus, if the reference classes were chosen poorly the forecasting result will give invalid results. <ref name="problem "/> Another factor to consider is having outliers in the identified samples. For instance, if the forecasting result falls within the insignificant region where the outlier stands, the RCF methods most likely will generate faulty predictions. Gathering a sufficient amount of reference class data can be challenging due to the lack of transparency and finding relevant classes. The issue here is, the time and country of the reference class data should be examined. For instance, data from similar old projects may not be relevant due to changes in material cost. <ref name="problem "/> Last but not least, the RCF method is more convenient in cases where errors are due to non-random events such as human bias in decision making while uncertainty is present.<ref name="sciencedirect hydroelectric"/> | ||
==Annotated Bibliography== | ==Annotated Bibliography== | ||
'''Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews.''' <ref name="Flyvbjerg2004" /> | '''Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews.''' <ref name="Flyvbjerg2004" /> | ||
* An overview of statistical studies on 258 large projects | * An overview of statistical studies on 258 large projects | ||
| − | * Relationship between project cost escalation | + | * Relationship between project cost escalation, sluggish project, and big project. |
| + | |||
| + | ''' Walczak, R. and Majchrzak, T., 2018. Implementation of the Reference Class Forecasting Method for Projects Implemented in a Chemical Industry Company. Acta Oeconomica Pragensia''' <ref name=" Chemical Industry"/> | ||
| + | * The correlation between poor performance and management | ||
| + | |||
| + | ''' Flyvbjerg, B., 2013. Over budget, over time, over and over again: Managing major projects. ''' <ref name="Flyvbjerg 2013"> "Flyvbjerg, Bent. "Over budget, over time, over and over again: Managing major projects." (2013): 321-344.https://www.researchgate.net/publication/235953357_Over_Budget_Over_Time_Over_and_Over_Again_Managing_Major_Projects" </ref> | ||
| + | * Optimism bias and strategic misrepresentation, | ||
| + | * What RCF does from a statistical perspective | ||
''' Flyvbjerg, B., 2007. Policy and planning for large-infrastructure projects: problems, causes, cures. Environment and Planning B: planning and design.''' <ref name="Flyvbjerg 2005" /> | ''' Flyvbjerg, B., 2007. Policy and planning for large-infrastructure projects: problems, causes, cures. Environment and Planning B: planning and design.''' <ref name="Flyvbjerg 2005" /> | ||
| Line 44: | Line 135: | ||
* Reference class forecasting | * Reference class forecasting | ||
| − | ''' | + | ''' Awojobi, O. and Jenkins, G.P., 2016. Managing the cost overrun risks of hydroelectric dams: An application of reference class forecasting techniques. Renewable and Sustainable Energy Reviews''' <ref name = "sciencedirect hydroelectric"/> |
| − | * | + | * Application of RCF in hydroelectric dams |
| − | + | ||
| − | |||
| − | |||
| − | |||
''' Pindy Bhullar, 2018, De-risking the programme portfolio with reference class forecasting''' <ref name="De-risking" /> | ''' Pindy Bhullar, 2018, De-risking the programme portfolio with reference class forecasting''' <ref name="De-risking" /> | ||
* An article about the poor performance of project and program and how can the RCFM be used | * An article about the poor performance of project and program and how can the RCFM be used | ||
| − | ''' | + | ''' Hájek, A., 2007. The reference class problem is your problem too. Synthese ''' <ref name="problem "> "Hájek, A., 2007. The reference class problem is your problem too. Synthese, 156(3), pp.563-585.https://link.springer.com/article/10.1007/s11229-006-9138-5" </ref> |
| + | * The problem of the reference class forecasting method from a statistical point of view | ||
==References== | ==References== | ||
<references /> | <references /> | ||
Latest revision as of 21:34, 28 February 2021
Contents |
[edit] Abstract
The definition of project success according to the standard published by the project management institute is meeting customers' expectations without exceeding the desired requirement such as cost, duration, and scope.[1] However, executing projects on time and within the estimated budget is a challenging aspect of project management. On that matter, a research was conducted by the Danish professor Bent Flyvbjerg to study the reasons for cost and time overrun in megaprojects. Flyvbjerg proposed the so-called Reference Class Forecasting to overcome these challenges. Reference class forecasting (RCF) is a method that studies the overall view of a certain project by forecasting similar projects rather than focusing solely on the considered project. [2] This method assists managers to make decisions under uncertainties by assessing the risk of the planned project. [1] In this article, the root causes of the managerial problem will be presented based on statistical studies on project failures in terms of budget and time of completion, after highlighting the need for improvement in this particular. The big idea which is the RCF technique and its three-step approach will be presented. That will be followed by a case study to get a better understanding of the RCF application. Lastly, the problem of using the RCF method will be presented.
[edit] Root causes of poor performance
Research made on a sample of 258 large projects executed over the last 7 decades shows that 90% of these projects exceeded the original budget. According to re-searcher, almost all projects do not deliver the intended promises such as on-time completion and staying within budget. [3]. The poor performance of a project is correlated to the managerial level such as project implementation and management methodology. [4] Project failures are usually covered up and overlooked. However, Flyvbjerg has identified two explanatory models for the poor performance of a project. [5] These models are:
[edit] Optimism bias
This model accounts for the benefit shortfalls that are caused by planning fallacy and optimism bias. Optimism bias is a term coined by Daniel Kahnemann means that people tend to see the world in a more positive light. Flyvbjerg states that managers make decisions based on optimism and planning fallacy rather than rational gain and statistical probabilities due to overconfidence. That leads to underestimating cost, completion times, and risks of planned actions. These biases are most likely generated by focusing on the so-called "inside view" and considering the project at hand as one of a kind. Thus, planners who pursue initiative will most likely end up overrunning the estimated budget and duration [5] Anchoring and adjustment cause also biases of judgment. In the context of planning, the first estimate acts as a benchmark for a later stage estimate. That results in making adjustments that are not compatible with the reality of the project performance.
[edit] Strategic misrepresentation
This model accounts for unreliable planning and decision-making due to political pressure. When estimating the outcome of a project, planners tend consciously to overestimate the benefits and underestimate the cost to increase the likelihood of getting their projector plan approved. [2] Thus, when political and organizational pressure are high, planners or project managers non-intentionally tend to underestimate the project cost and overestimate the benefits. However, to gain approval or funding, they intentionally use the following formula: [5]
Project approval = Underestimated cost + Overestimated benefits [5]
Poor performance can also be caused due to a technical error. For instance, unsuitable forecasting techniques, inadequate data, poor contract, etc. [2] However, this aspect of poor performance is beyond the scope of this article.
[edit] Big idea
Project managers should eliminate cognitive biases and reduce inaccuracy when making decisions, one method that is being used in infrastructure projects is Reference Class Forecasting. [4] In this section, the RCF model will be explained followed by the three-steps implementation
[edit] Reference Class Forecasting
The reference class forecast provided an external point of view and act as an enabler of better planning based on historical data of projects that have similar attributes. By doing so, the project managers can reduce biases that are caused due to assessing available information "inside views" and neglecting unknown unknowns or other considerations "outside views".[2] RCFM is recommended by the American Planning Association which “encourages planners to use reference class forecasting in addition to traditional methods as a way to improve accuracy“. [2] This method of enhancing decision-making in light of un-certainties has proved to be effective. It allows for adjustments to be made in the original cost-benefit analysis (CBA) so the plan includes margin errors. [6] This method attempts to fit a certain event into a probability of distribution of comparable class reference. However, from a statistical perspective, the reference class means prediction higher than the ordinary forecast estimate as it can see in figure 1. Also, the reference class prediction spreads the estimate of the conventional forecast interval. The reference class distribution is indicated by the dotted curve while the project promoters’ forecast, indicated by the dashed curve. [5]
[edit] Three steps approach
RCFM requires a large amount of work and should be implemented before initiating a project in order to get a unique opportunity on reflecting on the budget and planned duration. Implementing the RCFM requires a three-step approach, these steps are shown in figure 1 and explained thoroughly in the text below.
- Identify a reference class that has similar attributes to the project on hand. There is no role of thumbs when choosing a reference class. However, the reference class can not be narrow to get a reliable result if the categories were too small. The reference class can not be too wide either. Furthermore, the organization must also decide whether they want to create reference classes based on their projects within the programs or do they want to include reference classes from other organizations. [7]
- Determine a probability of distribution for the chosen reference classes. This requires trustful historical data from several projects within the reference class. The result of the probability distribution of the historical data will be used to estimate the level of uncertainty. From a statistical perspective, regression models are an essential tool in deriving the probability distribution. The empirical data is then utilized to establish the required optimism bias uplift. The uplift corresponds to the acceptable risk of cost and time overrun. [2]
- Comparing the project on hand with the reference class distribution in order to determine the desired outcome such as budget and project duration.[2]
[edit] Application
In this section, a practical application of the reference class forecasting method in planning large dams will be illustrated briefly. The analysis is based on a data set constructed from the world Bank and consists of 58 dam projects located in 33 developing countries and constructed between 1976-2005. The case study conducted to derive an outside view of cost uncertainty for three major development regions -Africa, Asia, and Latin America. The study follows the three RCF steps approaches in addition to a further innovatory step of fitting multivariate multilevel models to the reference data in order to predict future cost and time of completion. The reason for fitting regression models to the historical data is to enable the managers to focus on specific project-level risk instead of risk in a reference class. Consequently, project managers can base their decisions on empirical data rather than their own judgments and optimism. The study aims to generate three different probability distributions covering each of the three development regions. [6] However, this technique can be generalized and applied to different large-scale projects. Therefore, this section will highlight the framework, which is illustrated in figure 2, and avoid a detailed explanation of the case study result.

[edit] Step 1: Inputs
The project is initiated by analyzing the level of cost and time overrun in the completed projects, then a simple univariate analysis is conducted to classify the relationship between cost and time performance and project characteristics. In the dams example, they identified the project cost as follows: Cost = f (site- geology, size, time, price-inputs) where the site- geology has been identified as a significant variable that causes a direct impact on the cost overrun.[6]
[edit] Step 2: Output
The relationship between different projects can vary greatly across major groups. However, to capture the random effects in the dataset and to estimate the relationship between the different factors, hierarchical linear model HLM regression will be used. The regression model estimates the correlation between projects across sub-groups. For example, the causes of exceeding the budget in several projects in one country will most likely be similar. The cost and time of completion are then investigated using simple statistic tests and by fitting a multilevel regression model. The multi-level regression model allows correlation between estimate error within each sub-group. For instance, if the data set contains several projects from the same county, there is a high chance that the error of estimation will be similar across these projects. [6]
The result of the regression will be used to derive the probability distribution function. Considering the case of the dams, the forecast errors were distributed as the table below shows.
| Africa | Latin | Asia | ||||
| Margine of forecast error | Frequency | Rel Frequency | Frequency | Rel Frequency | Frequency | Rel Frequency |
| More than 10% | 9 | 69% | 12 | 80% | 17 | 77% |
| More than 20% | 7 | 54% | 12 | 80% | 11 | 50% |
| More than 50% | 2 | 15% | 7 | 47% | 1 | 4% |
To summarize the result of all projects combined
- 79% of the projects constructed have an error in cost projection more than 10%
- 62% of the projects constructed have an error in cost projection more than 20%
- 19% of the projects constructed have an error in cost projection more than 50%
[edit] Step 3: Decision
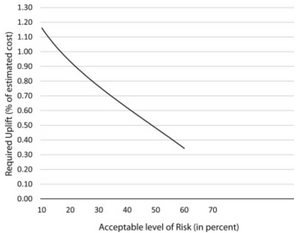
From the conducted analysis, we can conclude that there is misestimation in the project's cost. However, in this phase, the RCF method is used to improve the quality of decisions on dams. To do so, the level of uplift required will be determined based on the probability distribution of cost overrun. The acceptable level of risk in the dams constructed in Africa is shown in figure 3, the figure illustrates that, if the project manager wants to the tolerance for the decision as a 10% deviation of the actual cost then a 47% uplift will be required. The table below shows the required uplift for the three reference class according to several acceptable levels of risk tolerance. [6]
| Refernce class | Level of tolerance for risk | Uplift |
| Africa | 10% | 47% |
| Latin America | 10% | 117% |
| Asia | 10% | 54% |
Lastly, to correct the estimate about the budget, the level of uplift required should be determined in order to eliminate the biases in cost and time estimates [6]
[edit] Limitation
RCF is not a new tool within the decision-making framework for mega infrastructure projects. However, its application to other fields is rare due to the lack of data on relevant reference classes or faulty information. [6] Alan Hájek has categorized the problem of RCF in probability theory into frequentism, classical, logical, propensity, subjectivism. These problems are stated and explained from a statistical point of view. However, frequentism and subjectivism are still relevant to explain briefly in this article. [8]
[edit] Frequentism
Probabilistic frequentism defines the probability of an event as the limit of its relative frequency. Since each event has an unlimited number of properties and attributes, then the event will be classified into an endless number of classes. To forecast the outcome of future events, first, we should find a suitable reference class. However, the forecasted event can be incorporated in several reference classes and each of them has its own probabilities. This problem grows bigger when the probabilities of these classes differ greatly from one another. [8]
[edit] Subjectivism
The accuracy of the result generated by applying the RCF depends greatly on the sample size of the reference classes and the relevance of the reference class. Thus, if the reference classes were chosen poorly the forecasting result will give invalid results. [8] Another factor to consider is having outliers in the identified samples. For instance, if the forecasting result falls within the insignificant region where the outlier stands, the RCF methods most likely will generate faulty predictions. Gathering a sufficient amount of reference class data can be challenging due to the lack of transparency and finding relevant classes. The issue here is, the time and country of the reference class data should be examined. For instance, data from similar old projects may not be relevant due to changes in material cost. [8] Last but not least, the RCF method is more convenient in cases where errors are due to non-random events such as human bias in decision making while uncertainty is present.[6]
[edit] Annotated Bibliography
Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews. [3]
- An overview of statistical studies on 258 large projects
- Relationship between project cost escalation, sluggish project, and big project.
Walczak, R. and Majchrzak, T., 2018. Implementation of the Reference Class Forecasting Method for Projects Implemented in a Chemical Industry Company. Acta Oeconomica Pragensia [4]
- The correlation between poor performance and management
Flyvbjerg, B., 2013. Over budget, over time, over and over again: Managing major projects. [5]
- Optimism bias and strategic misrepresentation,
- What RCF does from a statistical perspective
Flyvbjerg, B., 2007. Policy and planning for large-infrastructure projects: problems, causes, cures. Environment and Planning B: planning and design. [2]
- Reasons of inaccuracy in forecasts of cost and benefits
- Reference class forecasting
Awojobi, O. and Jenkins, G.P., 2016. Managing the cost overrun risks of hydroelectric dams: An application of reference class forecasting techniques. Renewable and Sustainable Energy Reviews [6]
- Application of RCF in hydroelectric dams
Pindy Bhullar, 2018, De-risking the programme portfolio with reference class forecasting [7]
- An article about the poor performance of project and program and how can the RCFM be used
Hájek, A., 2007. The reference class problem is your problem too. Synthese [8]
- The problem of the reference class forecasting method from a statistical point of view
[edit] References
- ↑ 1.0 1.1 "Project Management Institute (PMI),2017, Guide to the Project Management Body of Knowledge (PMBOK® Guide) (6th Edition)"
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 " Flyvbjerg, B., 2007. Policy and planning for large-infrastructure projects: problems, causes, cures. Environment and Planning B: planning and design. http://documents1.worldbank.org/curated/en/968761468141298118/pdf/wps3781.pdf"
- ↑ 3.0 3.1 "Flyvbjerg, B., Skamris Holm, M.K. and Buhl, S.L., 2004. What causes cost overrun in transport infrastructure projects?. Transport reviews https://doi.org/10.1080/0144164032000080494a"
- ↑ 4.0 4.1 4.2 "Walczak, R. and Majchrzak, T., 2018. Implementation of the Reference Class Forecasting Method for Projects Implemented in a Chemical Industry Company. Acta Oeconomica Pragensia. https://www.researchgate.net/publication/324337008_Implementation_of_the_Reference_Class_Forecasting_Method_for_Projects_Implemented_in_a_Chemical_Industry_Company"
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 "Flyvbjerg, Bent. "Over budget, over time, over and over again: Managing major projects." (2013): 321-344.https://www.researchgate.net/publication/235953357_Over_Budget_Over_Time_Over_and_Over_Again_Managing_Major_Projects"
- ↑ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 "Awojobi, O. and Jenkins, G.P., 2016. Managing the cost overrun risks of hydroelectric dams: An application of reference class forecasting techniques. Renewable and Sustainable Energy Reviews. https://www.sciencedirect.com/science/article/pii/S1364032116301162/"
- ↑ 7.0 7.1 "Pindy Bhullar, 2018, De-risking the programme portfolio with reference class forecasting. https://www.apm.org.uk/news/de-risking-the-programme-portfolio-with-reference-class-forecasting/"
- ↑ 8.0 8.1 8.2 8.3 8.4 "Hájek, A., 2007. The reference class problem is your problem too. Synthese, 156(3), pp.563-585.https://link.springer.com/article/10.1007/s11229-006-9138-5"