Net Present Value (NPV)
(→Decision rule) |
(→Decision rule) |
||
| Line 101: | Line 101: | ||
If NPV = 0 The investment just returns the cost of capital. No increase or decrease in wealth results. This project adds no monetary value. Difficult to get the decision whether to accept or reject the project. Decision should be based on other criteria. | If NPV = 0 The investment just returns the cost of capital. No increase or decrease in wealth results. This project adds no monetary value. Difficult to get the decision whether to accept or reject the project. Decision should be based on other criteria. | ||
If NPV < 0 An implementation would destroy value (profit) in an amount equal to the negative NPV. The investment can be turned down. | If NPV < 0 An implementation would destroy value (profit) in an amount equal to the negative NPV. The investment can be turned down. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 113: | Line 107: | ||
! style="color:black" | Condition | ! style="color:black" | Condition | ||
! style="color:black" | Idea | ! style="color:black" | Idea | ||
| + | ! style="color:black" | Decision | ||
|- | |- | ||
|Orange | |Orange | ||
Revision as of 18:23, 14 February 2022
Written by Deepthi Tharaka Parana Liyanage Don- s203116
Contents |
Abstract
Financial appraisal is a method used to evaluate the viability of a proposed project or portfolio of investment projects by evaluating the benefits and costs that result from its execution. Investment decisions of the management are critical to a company since it decides the future of the company. This article discusses the Net Present Value (NPV) method which is widely used in financial appraisal. NPV is a dynamic financial appraisal method that considers the time value of money by applying discounting and compounding of all payment series during the investment period[1]. In simple terms, the net present value is the difference between an investment object’s incoming and outgoing payments at present time. NPV is determined by calculating the outgoing cashflows (costs) and incoming cash flows (benefits) for each period of an investment. After the cash flow for each period is calculated, the present value (PV) of each one is achieved by discounting its future value using the suitable discount rate. Net Present Value is the cumulative value of all the discounted future cash flows[2].
Firstly, this article discusses the idea behind the Net Present Value method. Then this introduces the NPV calculation method[1] and describes the importance of the variables in the formula such as discount rate. Also, it highlights the decision criteria behind NPV and explains it with a real-life application. Finally, it critically reflects on the limitations of this method and briefly introduces the other alternative financial apprisal methods such as Internal Rate of Return (IRR), payback method, and Return on Investment (ROI).
Big Idea
Project business case development is a critical point in a project where it uses to obtain the approval for investment in the project by presenting the benefits, cost, and risk associated with alternative options and the method of selecting the preferred solution. In a business case, financial appraisal plays a key role to answer the fundamental economic questions of whether an investment should be made and which project should be chosen among a selection of different alternatives. Because the task of financial appraisal is to predict the financial effects of planned investment and to present the data in such a way that a reasoned investment decision can be reached[1]. The net present value (NPV) method is the most frequently used approach in the financial appraisal of a project.
What is NPV?
Net Present Value (NPV) is the present value of the future net cash flows of an investment project. In simple terms, the net present value (NPV) is the difference between the present value of all future incoming cash flows and the present value of all future outgoing cash flows. NPV is a widely used method in financial appraisal that considers the time value of money by applying discounting or compounding of all payment series during the investment period[3].
Time value of money
Time value of money means that a sum of money is worth more now than the same sum of money in the future. That is because the money you have now can use it to make more money by running a business, buying something now and selling it later for more, or simply putting it in the bank and earning interest. Money can grow only through investing and investment delay is an opportunity cost where not having the money right now also includes the loss of additional income, which could be earned by simply having cash earlier. [invest-change]Future money is also less valuable because inflation erodes its buying power. Moreover, receiving money in the future rather than now may involve some risk and uncertainty regarding its recovery. For these reasons, future cash flows are worth less than the present cash flows. NPV assesses the profitability of a given project on the basis that cash flow in the future is not worth the same as a cash flow today. The time value of money is recognized in NPV by applying discounting or/and compounding to all payment series during the investment period[3].
Formula
The following formula use these common variables [1]:
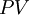 – Present Value
– Present Value
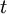 - time of the cashflow
- time of the cashflow
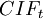 - Cash inflows in period t
- Cash inflows in period t
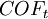 – Cash outflows in period t
– Cash outflows in period t
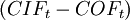 =
= 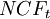 – Net cashflow in period t
– Net cashflow in period t
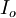 – Investment in t=0
– Investment in t=0
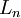 – Liquidation proceeds in t=n
– Liquidation proceeds in t=n
 – The discount rate
– The discount rate
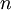 – Total number of periods
– Total number of periods
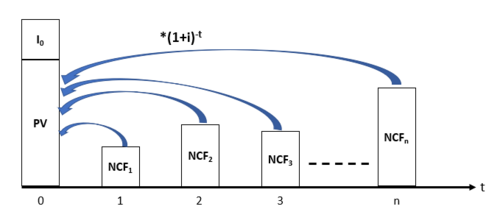
In order to consider the time value of money the net present value method considers the value of an investment at the present time by converting all information of the future into a key figure at the time today. This projection of the value that a future cash flow has in the present is called "present value" (PV).
Projection figure
To get the Present value (PV) of a future net cash flow in period t, they are discounted using discount rate(i):
Net present value combines these projections of net cash flows to assess the overall value of a project from the present view. In simple terms, The net present value is calculated from the difference of the present value of all future incoming cash flows(revenues/benefits) and the present value of all future outgoing cash flows(costs).
The net present value is given by:
The difference between the cash inflows and cash outflows 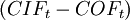 gives the net cash flow
gives the net cash flow 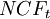 of the corresponding period. For normal investments which are characterized by initial investment
of the corresponding period. For normal investments which are characterized by initial investment 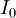 , discounting of the expected net cash flows
, discounting of the expected net cash flows 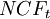 to t = 0 achieves comparability with the initial investment
to t = 0 achieves comparability with the initial investment 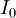 . Subtracting the initial investment outlay
. Subtracting the initial investment outlay 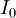 from the present value of the net cash flows gives the net present value (NPV). If a possible final payment
from the present value of the net cash flows gives the net present value (NPV). If a possible final payment 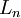 for the liquidation of the investment in t = n is also considered, the calculation of the net present value can formally be written as follows:
for the liquidation of the investment in t = n is also considered, the calculation of the net present value can formally be written as follows:
As a summary, the following steps are recommended for the calculation of the Net present value[1]:
- Determination of the initial investment
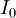 .
.
- Estimate the expected net cash flows
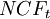 from the investment for each period of the planning horizon.
from the investment for each period of the planning horizon.
- Determination of the discount uniform rate
 (it is assumed that the discount rate remains unchanged over the life of the investment), in other words, the rate of return required by the investor.
(it is assumed that the discount rate remains unchanged over the life of the investment), in other words, the rate of return required by the investor.
- Determination of the present value through discounting of the expected net cash flows
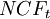 with the discount rate to the time period when the investment is made.
with the discount rate to the time period when the investment is made.
- Subtraction of the initial investment
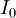 from the present value. This yields the net present value (NPV).
from the present value. This yields the net present value (NPV).
Note that This specification also allows the possible incorporation of payments from earlier periods and time periods t < 0 can also be considered. The discount factor 1/(1 + i)t is automatically converted into a compounding factor and the final value of all cash flows which occur before time 0 is correctly assessed in t = 0[1].
Other NPV Formula
NPV of an annuity
If the net cash inflows are uniform and equidistant and occur at the end of each period, the series of net cash flows can be interpreted as an annuity [1]. The payments or receipts occur at the end of each period for an ordinary annuity while they occur at the beginning of each period for an annuity due. Using the formula for the present value of an ordinary annuity, it follows that:
NPV of a perpetuity
For the special case that 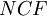 is considered as perpetuity, which is given for an infinite and constant stream of identical cash flows the NPV can be expressed as follows:
is considered as perpetuity, which is given for an infinite and constant stream of identical cash flows the NPV can be expressed as follows:
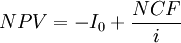
NPV with growing perpetuity
In the case where the net cash flows 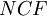 are growing indefinitely at the rate g (growth rate) with g < i the NPV can be obtained as:
are growing indefinitely at the rate g (growth rate) with g < i the NPV can be obtained as:
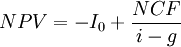
Discount Rate
The discount rate is the rate of return used to determine the present value of future cash flows in net present value calculation. The discount rate is a crucial component in determining NPV and the selection of discount rate will be company-specific as it is related to how the company gets its funds. Investments are financed using equity and/or debt and different costs of capital exist. If an investment is financed exclusively with equity, the discount rate can be derived from an alternative return available in the capital markets (cost of equity) or the average return of a similar investment object. Investments that are exclusively debt-financed can be assessed using the cost of debt to discount the net cash flows. If an investment relies on both equity and debt financing, the discount rate is the weighted average cost of capital (WACC) and can be calculated as weighted average of cost of equity and cost of debt. The weighted average cost of capital is often used in companies as the discount rate and it can be interpreted as the minimum rate of return that the investor demands for his activities. This is also commonly called the “hurdle rate” because for an enterprise to be profitable it has to earn a return greater than the cost of capital. [1].
However, it is appropriate to use higher discount rates to reflect other factors such as risk, opportunity cost of money invested in the infrastructure and etc [2]. An NPV calculated using variable discount rates (if they are known for the duration of the investment) may better reflect the situation than one calculated from a constant discount rate for the entire investment duration [1].
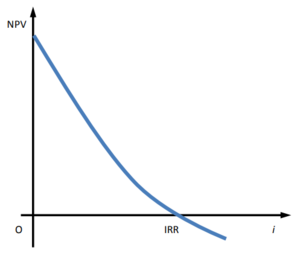
Also, it is important to highlight that the NPV depends on the choice about the discount rate, and on the time span considered by the analysis. The choice of the discount rate can dramatically change the net present value since the NPV is an inverse function of the discount rate (i). Higher the discount rate, the smaller the net present value. The time period of analysis influences the NPV because projects, in general, impose a negative cash flow in the first years and positive cash flows only sometime after its entering into operation, a longer period of analysis includes a bigger number of fiscal years with a positive cash flows than a shorter period of analysis [2].
Decision rule
Net present value is used to assess the attractiveness of the investment and it shows how much value an investment or project adds to the firm. If the Net Present Value (NPV) is positive (NPV > 0), it means that the benefits deriving from the project exceed the costs, then the project deserves to be done. The opposite happens if the NPV is negative (NPV < 0). If NPV = 0, it means that the project is not able to increase the value of the company and in this situation it is a better choice to avoid going on with the project [2].
Picture--
Condition Idea Decision If NPV > 0 Investment increase the value (profit) of the company in the amount of the net present value Investment can be made If NPV = 0 The investment just returns the cost of capital. No increase or decrease in wealth results. This project adds no monetary value. Difficult to get the decision whether to accept or reject the project. Decision should be based on other criteria. If NPV < 0 An implementation would destroy value (profit) in an amount equal to the negative NPV. The investment can be turned down.
| Condition | Idea | Decision |
|---|---|---|
| Orange | Butter | |
| Pear | Pie | |
| Apple | Ice cream |
The following two profitability criteria must be met for the economic viability of an investment[2]:
Absolute profitability: The Net Present Value of an investment option must be positive or at least zero (NPV≥ 0).
Relative profitability: The option with the highest positive NPV is the most profitable and usually the preferred option, provided that the investment risk is the same. Note that the net present values of different options can only be compared if their lifetime is the same.
Applications
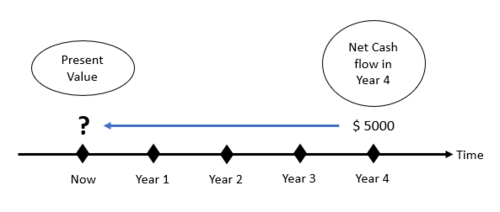
Calculation of Present value
For example, if a project is expected to receive $5,000 with 10% discount rate after 4 years, its present value (PV) can be calculated as:
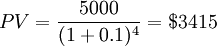
As per the above equation, (1+r) n is called the future value factor. There are pre-defined tables that specify the rate of interest and its value after ‘n’ number of years. It can also be utilized with the help of a calculator or an excel spreadsheet as well. The below snapshot is an instance of how the rate is calculated for different interest rates and at different time intervals.
Limitations
Introduce the limitations of NPV
Alternative financial appraisal methods
This section gives a brief idea about other methods
- IRR
- payback
- ROI
Annotated Bibliography
Reference Example: The book-1.[1] The book-2.[2] The book-3.[3] The book-4.[4] The book-5.[5]
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 Häcker J. and Ernst D., Ch. 8 - Investment Appraisal. In: Financial Modeling. Global Financial Markets., (Palgrave Macmillan, London, 2017), pp. 343-384, https://doi.org/10.1057/978-1-137-42658-1_8
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models., (Elsevier, 2018), pp. 85-114, https://doi.org/10.1016/C2016-0-03558-1
- ↑ 3.0 3.1 3.2 Konstantin P. and Konstantin M., Ch. 4 - Investment Appraisal Methods. In: Power and Energy Systems Engineering Economics., (Springer, Cham, 2018), pp. 39-64, https://doi.org/10.1007/978-3-319-72383-9_4
- ↑ Poggensee K. and Poggensee J., Ch. 3 - Dynamic Investment Calculation Methods. In: Investment Valuation and Appraisal., (Springer, Cham, 2021), pp. 85-140, https://doi.org/10.1007/978-3-030-62440-8
- ↑ Ing E. and Lester A., Ch. 6 - Investment Appraisal. In: Project Management, Planning and Control. 7th Edition., (Elsevier, 2017), pp. 29-36, https://doi.org/10.1016/B978-0-08-102020-3.00006-1
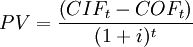
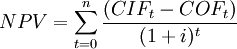
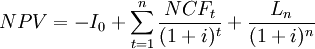
![N P V=-I_{0}+N C F \cdot\left[\frac{(1+i)^{n}-1}{i \cdot(1+i)^{n}}\right]+\frac{L_{n}}{(1+i)^{n}}](/images/math/f/b/b/fbb9818d6744581d2a9ff5023d8e9138.png)