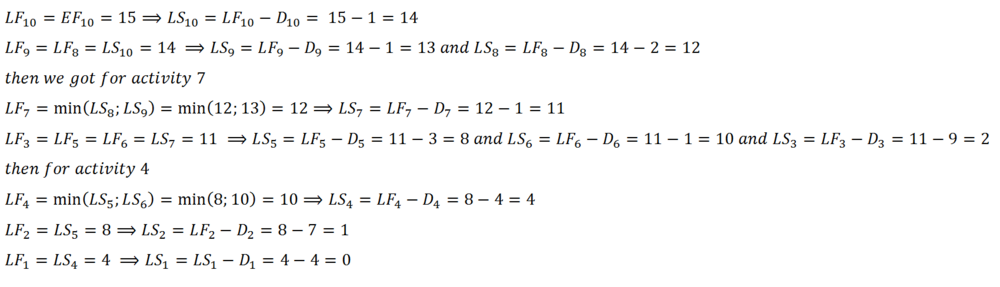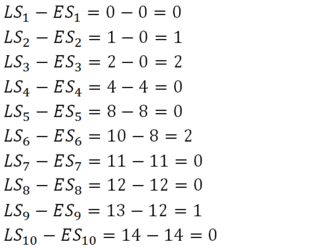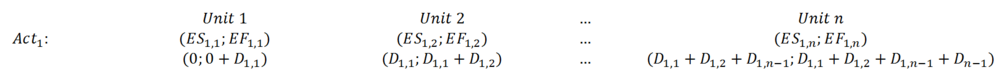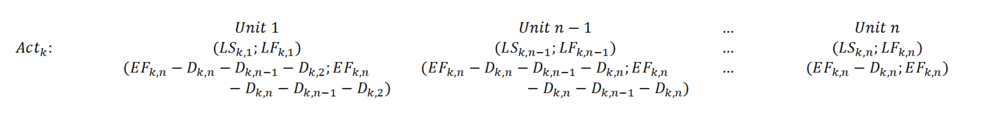Critical Path Method in Construction Industry
Adam.pekala (Talk | contribs) (→Resource-Activity Critical Path Method) |
Adam.pekala (Talk | contribs) (→Resource-Activity Critical Path Method) |
||
| Line 162: | Line 162: | ||
#* Flexible Resource Precedence Relation – relation in which a delay in finish time of pre-occurring activity results in delay of start time only, in following activity | #* Flexible Resource Precedence Relation – relation in which a delay in finish time of pre-occurring activity results in delay of start time only, in following activity | ||
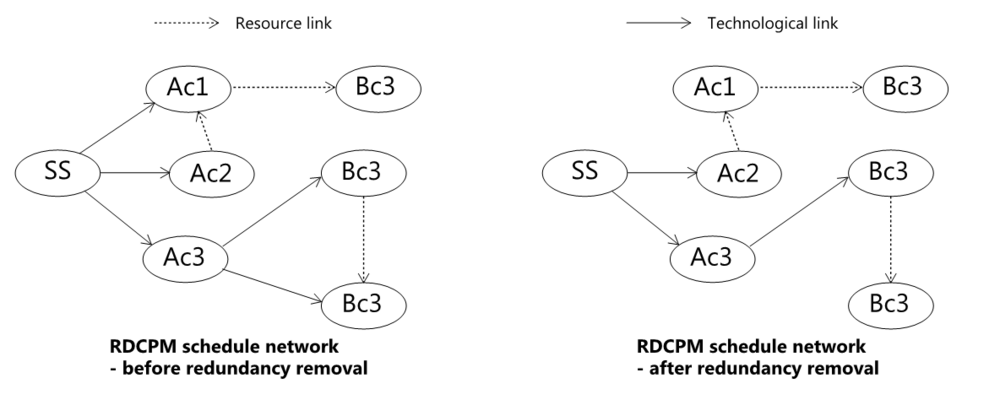
#Removal of redundant precedence relations – all of the redundant activities can be safely removed from the schedule. If an activity is preceded by two inter-dependent activities, one of the links can be safely removed. Example of link removal is presented below. | #Removal of redundant precedence relations – all of the redundant activities can be safely removed from the schedule. If an activity is preceded by two inter-dependent activities, one of the links can be safely removed. Example of link removal is presented below. | ||
| + | |||
| + | [[File:CPM Figure10.PNG|1000px|center|Figure 8: RDCPM - Redundancy]] | ||
| + | <div style="clear: both"></div> | ||
== Use Limitations == | == Use Limitations == | ||
Revision as of 05:07, 22 September 2015
Critical Path Method (CPM) is a project management method created in 1958 in American company DuPont to improve internal production processes. Since then the method is widely used in industries such as construction, aerospace, defense, engineering, research and many more. However, this article focuses on its use in civil engineering industry and construction. The method is suitable for all kind of construction projects that require many independent activities to be completed.
Critical path is a sequence of activities that lead to the shortest possible completion of the project. These activities are called critical activities and every delay in each of these activities will result in delay of the whole project. This article depicts ways of using the method to analyze projects as a several groups of activities to reduce the bottleneck points and finish the project on time and within the budget. Methodology of creation of the basic CPM direct acyclic graph (DAG) is presented in a way of short step-by-step tutorial.
Construction projects, although very complicated are similar or even identical in a way of having similar unit activities and resources. Scheduling in linear construction projects require use of aforementioned resources from one activity to another in such a way, that continuity and logic between network activities is sustained. In the article the procedure for CPM-based scheduling in linear construction projects is described and explained. Moreover, Resource Activity Critical Path Method (RACPM) is presented based on Hong Kong Polytechnic University practical method based on the additional dimension of time added to the dimension of time. As a summary, advantages and disadvantages of the method are described as well as limitations to the use of CP-method. At the end of the article annotated bibliography with reference links is provided.
Contents |
Big idea
Short history
While the method itself has been created in 1958 its induction to construction industry happened awhile later. There are always two stages recognized while implementing the method: first stage, when there has been an initial interest aroused in the industry and second, while the overall effects on the industry are known. It took as long as in 1968 when the method was known well enough to consider it to be in its second stage – mainly due to time-consuming characteristic of construction projects.[1] Nevertheless, the method was adapted to specifics of civil and construction projects’ characteristic and was successfully used in the industry ever since.
Evolution
What helped CPM to be more and more popular was that it was of great utility while managing bigger projects – the method was immediately implemented to projects of value higher than £100’000[1] (value from 1968, approx. £2’000’000 nowadays). The method itself has not changed much in terms of its methodology. Algorithms of calculation of critical path remain the same. What changed significantly is the use of the computers in its implementation to the projects. Back when the method was created hand calculations were common almost for all of the projects, at least for tender stages. Project managers mentioned from 50 up to 600 activities as a range for hand calculations using CPM. Nowadays various types of software is used i.a. Primavera[2], MS Project[3] or various spreadsheets.
General methodology
The Critical Path Method indicates sequence of activities that determine the earliest possible completion for analyzed project. The resulting sequence (or sequences – there might be more than one) is called the critical path. All of the activities are called critical activities and any delay in those will cause a delay for the project or phase in general. A guide to create the critical path is as follows:
- Identify the activities – a thorough check and investigation on every activity present in the project or stage should be made - project scope and details are helpful. Every activity should be described with duration.
- Activity sequence establishment – it is the most important step to create working and correct critical path. For this to be done correctly three questions should be answered:
- which tasks should take place before this task
- which tasks should be completed at the same time
- which tasks should happen immediately after this task
- Network diagram – it should be prepared based on the prepared sequence
- Activity completion time estimation - this value should be estimated based on the experience or resource catalogues. Since CPM is a deterministic model it does not take into account variation in the completion time - an exact number has to be put in.
- Identification of critical path – based on parameters such as Earliest Start Time, Earliest Finish Time, Latest Finish Time, Latest Start Time (to be explained in following chapter)
- Live updating of critical path diagram – all of the changes happening to the project should be implemented for the diagram and method to be accurate during whole project time
Graph creation method
Terminology and suggested layout
For CPM a natural representation of the critical path is a Directed Acyclic Graph[4]. This is a type of graph that is created by collection of vertices and direct edges in a way that there is no loop (no way to start at one activity and after following a sequence loop back to the same activity).
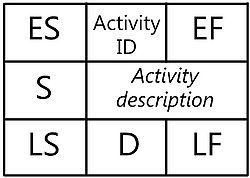
Graphs for CPM are specific type of PERT[5] graphs. However, in CPM the time of a single activity are identical and there is no distinguishing between optimistic, pessimistic and most likely time. For creating a network there are many types of activity boxes sugested, one of which is presented below.
Where:
- ID - Activity number
- ES - Earliest possible start
- EF - Earliest possible finish
- LS - Latest possible start
- LF - Latest possible finish
- D - Duration
- S - Slack
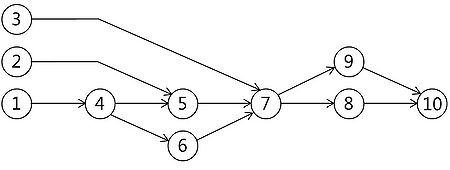
Example of CPM graph creation
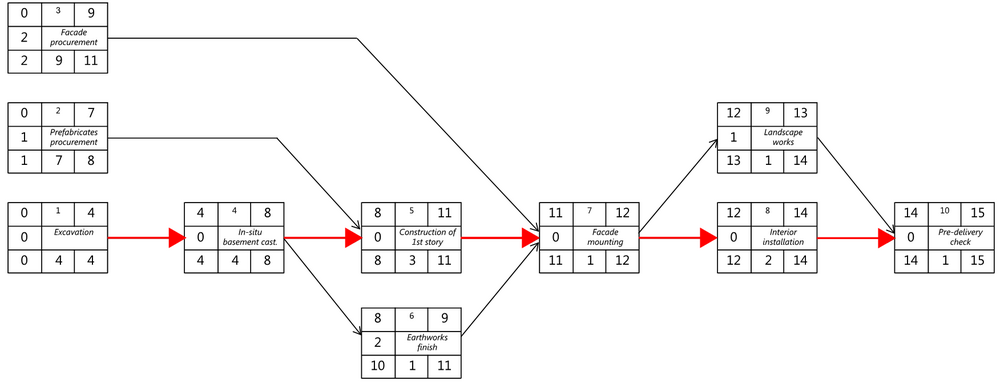
Based on a simplified one story building and reduced to basic number of activities a CPM method with CPM graph creation will be presented.
| ID/Number | Name/Description | Estimated duration |
| 1 | Excavation | 4 |
| 2 | Prefabricates procurement | 7 |
| 3 | Facade procurement | 9 |
| 4 | In-situ basement casting | 4 |
| 5 | Construction of 1st story | 3 |
| 6 | Finishing earthwork | 1 |
| 7 | Facade mounting | 1 |
| 8 | Interior instalation | 2 |
| 9 | Landscape works | 3 |
| 10 | Pre-delivery check | 1 |
There are two main steps to be performed based on the activities' duration provided in activity table - forward pass calculation and backwards pass calculation.
Forward pass calculation
As in the dependency tree there are three starting activities - all of them are granted starting time equal to zero. Then calculations to obtain ES and EF times are performed as follows:
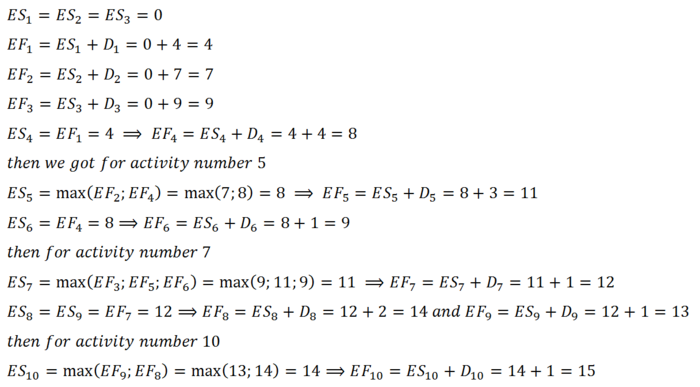
Based on the duration of single activity total project time has been derived and is equal to 15 weeks.
Backward pass calculation
Based on the total project time and single activity duration LF and LS times are derived. Calculations should follow method presented below:
Slack calculation
Based on values of ES and LS the possible slack is calculated. Slack is a delay time that will not cause any delay for the whole project. There is no slack on a critical path.
CPM Graph
Based on all of the information above a CPM graph is sketched. All of the activities with no slack are called critical activities and the sequence of those is called critical path - marked red on the graph.
Resource based CPM scheduling in linear projects in constrction
Intoduction and differences
Construction projects, although made as "one-off" and completely different from each other are very similar in a way of repeating processes within one project. Multi-storey buildings, highways being built stage by stage or even gas pipelines. All of them have linear, repetitive characteristics and they require special approach in scheduling. Critical Path Method provides the scheduler with slack/free float time, times of earliest start or finish but it assumes unlimited resources. Scheduling of a construction projects has to be made while keeping in mind not only continouos use of resources but also the logic between activities at the same time. The most useful and most convenient method to do so is Line of Balance or Linear Scheduling Method. Created in early 1940s and developed in 1952 and 1960 by US Navy with the idea of evaluating production lines - processes with lots of repetitions and using series of workstations. It took as long as to 2004 while The National Agency of the United Kingdom implemented it for repetitive housing units[6]. The methodology and rules for Linear Critical Path Calculations are almost the same as for regular CPM. However, here calculations are based on activities divided in different stages. Combination of those will produce logical network with availability of resources and continuity of its usage.
Forward pass calculations
Foward pass calculations are driven the same logic as for regular CPM. However, the calculations are divided for different activities and substages of the activities. The linear method assumes that as soon as one stage is finishd, the second stage should follow immediately. Below there are First Activity calculations presented in division for n-stages.
More of the calculation steps and thorough methodology including lags and delays can be followed in the technical paper of Journal of the South African Institution of Civil Engineering[6].
Backward pass calculations
The backward pass in linear scheduling goes from the last stage in last activity and follows the same logic as for regular CPM. Below there are k-th activity calculations presented in division for n-stages.
More of the calculation steps and thorough methodology including lags and delays can be followed in the technical paper of Journal of the South African Institution of Civil Engineering[6].
Linear schedule example
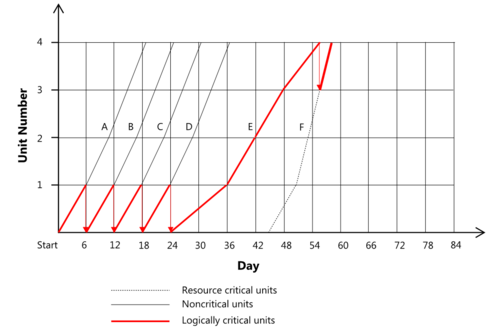
Known from CPM activities with no float time are considered critical. However, contrary to linear scheduling, CPM cannot maintain resource continuity as it focuses basically on satisfying logical dependecies and might be adjusted afterwards by resource availability criteria. Linear projects require continuous usage of resources what leads to two types of criticalities - logic criticalities (defined by CPM) and resource criticalities. If any of the activities is resource critical according to linear scheduling, it will be delayed and cause the whole project to delay. On this basis some of the non-critical CPM activities might become critical in linear schedules.
A way of showing the dependencies is by drawing differently sloped lines on graphs. This procedure for linear-CPM graph is completely user-based and does not follow any strict algorithm. Here the scheduler defines the critical activities (both logically and resource dependent) and places them on the graph based on calculated previously values of Early/Late Start and Finish times.
Based on the sample graph with 6 activities divided into 4 stages each there are following criticalities:
- A1, B1, C1, D1, E1-E4 and F4 are logically critical due to inter-actvity dependencies
- F1-F3 were scheduled as resource dependent to provide resource continuity. If any of these activities is delayed, E4 (critical path) will be delayed
- remaining activities are non-critical. If they are delayed they will disturb resource continuity, not the delivery time.
Resource-Activity Critical Path Method
Since as mentioned in Linear Resource Based CPM chapter it is impossible to identify corrects slacks and critical path which is resource based using regular CPM method further studies were undertaken and 4-step resource dependent critical path method was created (RDCPM). This method, however, was constrained by assumption of maximum resources being available during the whole duration of a project. A new method was created and called Enhanced RDCPM [7] - taking from the traditional CPM and Resource Constrained Scheduling. It is divided in 6 steps which are as follows:
- Performing CPM – standard analysis is performed with forward and backward pass to calculate ES, EF, LS, LF and floats for each of the activities.
- Inserting Dummy Activities – if the project has varying resources during its execution it might be impossible to identify resource dependencies for activities. It is inserted in-between the periods where the availability of the resources varies – classic RCS can be easily used. Moreover dummy activities might help to establish resource links between activities so that the schedule is easily updateable.
- RCS forward pass calculation – based on previously performed steps RCS forward calculation is performed to set the maximum available resources and omit resources that are overloaded. More information about the process can be found in [7]
- RCS backward pass calculation – RCS backward pass is performed to establish resource constrained LSj and LFj based only on original CPM ES and EF.
- Resource Dependency identification – Authors of the enhanced RDCPM indicate two different dependencies that exist in the projects.
- Strict Resource Precedence Relation – relation in which a delay in finish time pre-occurring activity results in delay in finish time of following activity
- Flexible Resource Precedence Relation – relation in which a delay in finish time of pre-occurring activity results in delay of start time only, in following activity
- Removal of redundant precedence relations – all of the redundant activities can be safely removed from the schedule. If an activity is preceded by two inter-dependent activities, one of the links can be safely removed. Example of link removal is presented below.
Use Limitations
Advantages and disadvantages
Conclusions
Bibliography and further links
- ↑ 1.0 1.1 [1] “Critical path analysis and the civil engineering industry, D.H.Wade, ICE Proceedings, Volume 39, Issue 2, 01 February 1968 , pages 289 –303”
- ↑ [2] Primavera P6 Scheduling
- ↑ [3] MS Project
- ↑ [4] Directed Acyclic Graph
- ↑ [5] Program Evaluation and Review Technique
- ↑ 6.0 6.1 6.2 [6] “A procedure for critical path method-based scheduling in linear construction projects” On-line version ISSN 2309-8775
- ↑ 7.0 7.1 [7] Enhanced Resource-Dependent Critical Path Method for Identifying Resource Dependencies in Variable Resource Constrained Project” Journal of Japan Society of Civil Engineers, Ser. F3 (Civil Engineering Informatics) Vol. 69 (2013) No. 2 p. I_110-I_120
Sample Code snips
This is a list
- List1
- List2
- List2
This is a picture
This is big, italian and underlined * You can choose to work on one of two types of articles: *
Here's some links
Articles Fall Term 2015 User's Guide Configuration settings list MediaWiki FAQ MediaWiki release mailing list Help Content
Aaanndd some references