Data-Driven Decision-Making under Uncertainty
| Line 7: | Line 7: | ||
. | . | ||
====Minimax Criterion==== | ====Minimax Criterion==== | ||
| − | . | + | The Minimax or Maximin approach shows a pessimistic conception: Thus, only the worst possible outcome of each alternatives is considered and compared with the others. |
| + | |||
| + | |||
| + | (ref: Development of fuzzy multi-criteria approach) | ||
| + | |||
| + | |||
====Maximax Criterion==== | ====Maximax Criterion==== | ||
. | . | ||
Revision as of 17:14, 6 February 2023
Developed by Anton Reiling
There are several approaches to reach decisions under uncertainty under the assumption of reliable, fixed data. The Minimax and Maximax criterion simply consider the worst or best possible outcome of decision alternatives. The Hurwicz Criterion offers a mix between these two approaches depending on the predefined Optimism Parameter. The Minimax Regret Criterion considers the opportunity costs caused by choosing an alternative to reach a decision and the Laplace Criterion compares the expected values of the alternatives. These approaches can be used within Project, Program and Portfolio Management, for example to compare to offers for Outsourcing Contracts. However, due to simplifications and assumptions these methods are limited to rather simple problems with low complexity. This is because they lack the possiblity to assess risk, qualitative inputs and heterogenous probabilities for different outcomes.
Contents |
Decision-Making Approaches
.
Minimax Criterion
The Minimax or Maximin approach shows a pessimistic conception: Thus, only the worst possible outcome of each alternatives is considered and compared with the others.
(ref: Development of fuzzy multi-criteria approach)
Maximax Criterion
.
Hurwicz Criterion
.
Minimax Regret Criterion
.
Laplace Criterion
.
Application to Outsourcing Contracts within Project Management
These approaches can also be applied to Project, Program and Portfolio Management. However, since they assume that the given data is certain per scenario and can be expressed as a number, the range of sensible application descreases. One example for utilizing these approaches are simple decisions regarding choosing suppliers for Outsourcing.
Let's take the following example to see how the different methods influence the decision which supplier to select: For a software project, parts of the front-end development are outsourced to a third-party supplier, which needs to be chosen according to their costs. Since mostly supplier and customer agree on a quotation with a cost estimate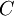 
, the resulting costs 
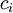can be higher or lower than the estimate, depending on incidents during the projects like delays, reworking or other unplanned costs. Of course, some additional costs are already included in the cost estimate to grant the supplier a buffer. This example will consider the following 5 scenarios:
- Scenario 1: Best scenario: None of the predicted costs actually occured:
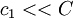
- Scenario 2: The actual costs are lower than the estimated costs, but not as low as
: 
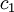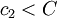
- Scenario 3: The actual costs match the estimated costs:
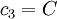
- Scenario 4: The actual costs are higher than the estimated costs, but not as high as
: 
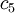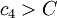
- Scenario 5: Worst scenario: On top of the predicted costs a high number of unexpected costs occurs which increases the overall costs drastically:
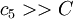
The following two suppliers can be chosen: Supplier A guarantees a fixed price of 100 monetary units, no matter which scenario will ocur (i.e. how many unexpected costs will occur). Supplier B however, proposes and estimated price of 100 monetary units. The actual price can vary depending on the scenario, which the following table illustrates:
| Suppliers | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| Supplier A | 100 | 100 | 100 | 100 | 100 |
| Supplier B | 80 | 95 | 100 | 105 | 150 |
Applying the described approaches to this problem yields the following results:
- Minimax Criterion:
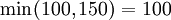→ Supplier A
- Maximax Criterion:
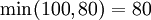→ Supplier B
- Hurwicz Criterion:
![[\min(a=2,s) * \lambda + \max(a=2,s) * (1-\lambda)] - [\min(a=1,s) * \lambda + \max(a=1,s) * (1-\lambda)] > 0 for \lambda < \tfrac{5}{7}](/images/math/2/5/8/258ef7438c7256016a87b95ece1b364e.png)
(→ Supplier A)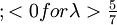 
(→ Supplier B)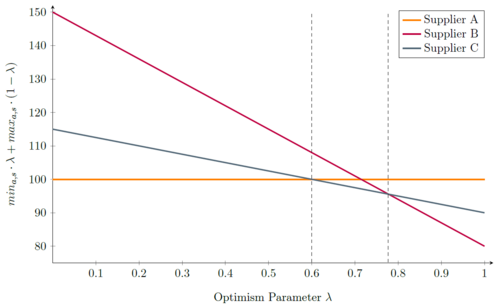 
- Minimax Regret:
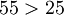→ Supplier A
- Laplace Criterion:
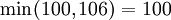→ Supplier A
It can be seen that due to the assymetric distribution towards higher average costs for Supplier B the Minimax Regret and the Laplace Criterion suggest to choose Supplier A. For the same reason the Hurwicz Criterion suggests to choose Supplier A for a higher Range in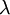 
than to choose Supplier B. Since we have costs independent from the scenario for Supplier A it stands to reason that the Minimax Criterion suggests Supplier A and the Maximax Criterion Supplier B.
It can be critisized that only the costs were considered in this example and not features like reliability or service quality. Also, all the outcomes were assumed to have an equal probablity of happening which is also rather unrealistic. Especially considering scenario 5 equally probable put a high weight on the 150 monetary units of Supplier B for this scenario. However, for minor supplier selection decisions these approaches provide results with low effort.
Limitations
.
Annotated bibliography
.
