Project viability assessment through Net Present Value (NPV)
(→Discount rate) |
(→NPV Formula) |
||
| Line 10: | Line 10: | ||
== NPV Formula == | == NPV Formula == | ||
| − | The net present value | + | The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments. <ref name="NPV_H"/> The formula used to calculate the net present value is presented below: |
<math>NPV = \sum_{t=0}^{N}\frac{B_t-C_t}{(1+r)^t}</math> | <math>NPV = \sum_{t=0}^{N}\frac{B_t-C_t}{(1+r)^t}</math> | ||
| Line 22: | Line 22: | ||
* <math> r</math>: The discount rate | * <math> r</math>: The discount rate | ||
| − | There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain Danish Crown tomorrow is less valuable than a Danish Crown today.<ref name="NPV_P"/> This is modulated by the use of the discount factor <math> (1+r)^t </math>, where a discount rate is used.<ref name="DSSA"/>Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to <math> t = 0 </math>. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, <math> N </math>.<ref name="NPV_P"/>.For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. | + | There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain Danish Crown tomorrow is less valuable than a Danish Crown today.<ref name="NPV_P"/> This is modulated by the use of the discount factor <math> (1+r)^t </math>, where a discount rate is used.<ref name="DSSA"/>Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to <math> t = 0 </math>. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, <math> N </math>.<ref name="NPV_P"/>.For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. This makes for a |
== Time value of money == | == Time value of money == | ||
Revision as of 21:47, 22 February 2023
Contents |
Abstract
The Net Present Value (NPV) is a widely used financial metric in project management. Its purpose is to evaluate the profitability of a proposed project by aggregating the streams of costs and benefits into a single value. This makes for an effective indicator of identifying profitable projects when assessing multiple projects at a time. For a given project to be considered a profitable investment, its NPV must be larger than zero. [1]
Central to the calculation of the NPV is assigning varying weights, dependent on time, to the benefits and costs through the utilization of a so-called discount factor, which is calculated using a discount rate. The discount rate represents the rate of interest that is used to discount all future costs and benefits. [2] By incorporating this principle, the NPV accounts for and subscribes to the paradigm of the time value of money, referring to the idea that money has a different value at different points in time.[3]
This article explores central concepts connected to the calculation and application of NPV in the assessment of projects, programs, or portfolios. For demonstration purposes, an example of the calculation of an emulated project's NPV will be given. Moreover, the advantages and disadvantages of using NPV as an indicator of project profitability will be addressed.
NPV Formula
The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments. [4] The formula used to calculate the net present value is presented below:
-
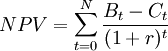
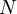:The calculation period of the project in years.
-
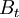: The aggregated amount of benefits (both positive and negative) in year t
-
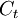: The amount of investments costs in year t
-
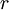: The discount rate
There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain Danish Crown tomorrow is less valuable than a Danish Crown today.[5] This is modulated by the use of the discount factor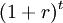 
, where a discount rate is used.[2]Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to 
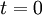. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, 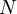.[5].For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. This makes for a
Time value of money
Brief explanation time value of money and how it relates to NPV
Discount rate
A succinct description of discount rate and it’s formula. Necessary to explain, to grasp the concept of NPV.
(For the peer-review reader, hi!; This is the beginning of the paragraph).
The discount rate is the interest rate used to convert future cash flows into an equivalent one-off upfront sum or present value (article 18). As the discount rate increases, the lower the present value of a given future amount becomes. Hence the magnitude of the discount rate exerts a significant influence on the net present value. For instance, if the selected discount rate level is set too high, it may make potentially good projects, programs or portfolios seem unattractive, whereas if set too low, it might result in the opposite.
Financial Appraisal
Why do we make financial appraisals of projects, programs, and portfolios? Where do NPV fit?
Application and decision making
In the following paragraph, the application of NPV in regard to assessing the profitability of a project prior to commencing it will be outlined.
Example
A practical example on how to calculate the NPV of a construction project.
Advantages
Disadvantages
Annotated Bibliography
References
- ↑ Investopedia. (2023). Net Present Value (NPV): What It Means and Steps to Calculate It. Investopedia, 1–8. https://www.investopedia.com/terms/n/npv.asp
- ↑ 2.0 2.1 Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.
- ↑ Gardner, N.D. 2004. The Time Value of Money: A Clarifying and Simplifying Approach. Journal of College Teaching & Learning (TLC). 1, 7 (Jul. 2004).
- ↑ Häcker, J., & Ernst, D. (2017). Financial Modeling. In Financial Modeling.
- ↑ 5.0 5.1 Žižlavský, O. (2014). Net Present Value Approach: Method for Economic Assessment of Innovation Projects. Procedia - Social and Behavioral Sciences, 156(April), 506–512.
