Project viability assessment through Net Present Value (NPV)

From apppm
(Difference between revisions)
Jump to: navigation, search
(→‎Discount rate)
(→‎Discount rate)
Line 197: Line 197:
 
|2.56
 
|2.56
 
|2.56
 
|2.56
−
|2.77
+
|2.77}
−
|}
+
  
 
== Financial Appraisal ==
 
== Financial Appraisal ==

Revision as of 20:46, 4 April 2023

Contents

Abstract

The Net Present Value (NPV) is a widely used financial metric in project management. Its purpose is to evaluate the profitability of a proposed project by aggregating the streams of costs and benefits into a single value. This makes for an effective indicator of identifying profitable projects when assessing multiple projects at a time. For a given project to be considered a profitable investment, its NPV must be larger than zero. [1]

Central to the calculation of the NPV is assigning varying weights, dependent on time, to the benefits and costs through the utilization of a so-called discount factor, which is calculated using a discount rate. The discount rate represents the rate of interest that is used to discount all future costs and benefits. [2] By incorporating this principle, the NPV accounts for and subscribes to the paradigm of the time value of money, referring to the idea that money has a different value at different points in time.[3]

This article explores central concepts connected to the calculation and application of NPV in the assessment of projects, programs, or portfolios. For demonstration purposes, an example of the calculation of an emulated project's NPV will be given. Moreover, the advantages and disadvantages of using NPV as an indicator of project profitability will be addressed.

NPV Formula

The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments. [4] The formula used to calculate the net present value is presented below:

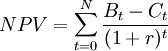
NPV = \sum_{t=0}^{N}\frac{B_t-C_t}{(1+r)^t}

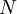  • N:The calculation period of the project in years.
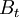  • B_t: The aggregated amount of benefits (both positive and negative) in year t
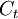  • C_t: The amount of investments costs in year t
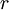  • r: The discount rate

There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain Danish Crown tomorrow is less valuable than a Danish Crown today.[5] This is modulated by the use of the discount factor 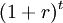(1+r)^t , where a discount rate is used.[2]Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to 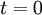t = 0 . The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, 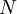N .[5].For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. This makes for a

Time value of money

Brief explanation time value of money and how it relates to NPV

Discount rate

A succinct description of discount rate and it’s formula. Necessary to explain, to grasp the concept of NPV.

(For the peer-review reader, hi!; This is the beginning of the paragraph).

The discount rate is the interest rate used to convert future cash flows into an equivalent one-off upfront sum or present value (article 18). As the discount rate increases, the lower the present value of a given future amount becomes. Hence the magnitude of the discount rate exerts a significant influence on the net present value. For instance, if the selected discount rate level is set too high, it may make potentially good projects, programs or portfolios seem unattractive, whereas if set too low, it might result in the opposite.

Base rates as of 1.4.2023
From To AT BE BG CY CZ DE DK EE EL ES FI FR HR HU IE IT LT LU LV MT NL PL PT RO SE SI SK UK
1.4.2023 … 3.06 3.06 1.51 3.06 7.43 3.06 3.54 3.06 3.06 3.06 3.06 3.06 3.06 15.10 3.06 3.06 3.06 3.06 3.06 3.06 3.06 7.62 3.06 8.31 3.21 3.06 3.06 3.52
1.3.2023 31.3.2023 3.06 3.06 1.10 3.06 7.43 3.06 2.92 3.06 3.06 3.06 3.06 3.06 3.06 15.10 3.06 3.06 3.06 3.06 3.06 3.06 3.06 7.62 3.06 8.31 2.96 3.06 3.06 3.52
1.2.2023 28.2.2023 2.56 2.56 0.79 2.56 7.43 2.56 2.92 2.56 2.56 2.56 2.56 2.56 2.56 15.10 2.56 2.56 2.56 2.56 2.56 2.56 2.56 7.62 2.56 8.31 2.44 2.56 2.56 2.77
1.1.2023 31.1.2023 2.56 2.56 0.36 2.56 7.43 2.56 2.92 2.56 2.56 2.56 2.56 2.56 2.56 15.10 2.56 2.56 2.56 2.56 2.56 2.56 2.56 7.62 2.56 8.31 2.44 2.56 2.56 2.77}

Financial Appraisal

Why do we make financial appraisals of projects, programs, and portfolios? Where do NPV fit?

Application and decision making

In the following paragraph, the application of NPV in regard to assessing the profitability of a project prior to commencing it will be outlined.

Example

A practical example on how to calculate the NPV of a construction project.

Advantages

Disadvantages

Annotated Bibliography

References

  1. ↑ Investopedia. (2023). Net Present Value (NPV): What It Means and Steps to Calculate It. Investopedia, 1–8. https://www.investopedia.com/terms/n/npv.asp
  2. ↑ 2.0 2.1 Barfod, M. B., & Leleur, S. (2019). Decision Support and Strategic Assessment DTU Management Compendium.
  3. ↑ Gardner, N.D. 2004. The Time Value of Money: A Clarifying and Simplifying Approach. Journal of College Teaching & Learning (TLC). 1, 7 (Jul. 2004).
  4. ↑ Häcker, J., & Ernst, D. (2017). Financial Modeling. In Financial Modeling.
  5. ↑ 5.0 5.1 Žižlavský, O. (2014). Net Present Value Approach: Method for Economic Assessment of Innovation Projects. Procedia - Social and Behavioral Sciences, 156(April), 506–512.
Retrieved from "http://wiki.doing-projects.org/index.php?title=Project_viability_assessment_through_Net_Present_Value_(NPV)&oldid=131101"
Personal tools
Namespaces

Variants
Actions
Navigation
Toolbox