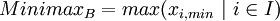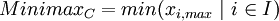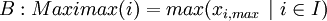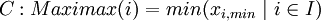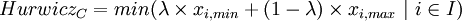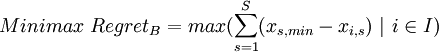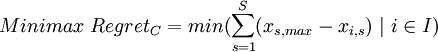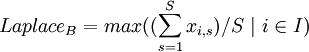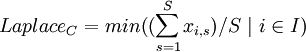Data-Driven Decision-Making under Uncertainty

Revision as of 17:51, 9 May 2023

Developed by Anton Reiling

Project, program and portfolio managers need to make countless decisions which are based on limited information. This article deals with different methods to choose the optimal decision alternative under uncertainty of events that might occur and deviate from an expected outcome. The degree of complexity and scope among the approaches differs considerably, which is why they should be selected according to the use case.

Starting with the simple approaches, the Minimax and Maximax criterion consider the worst or best possible outcome of decision alternatives. The Hurwicz Criterion offers a mix between these two approaches depending on the pre-defined Optimism Parameter. The Minimax Regret Criterion considers the opportunity costs caused by choosing an alternative to reach a decision, and the Laplace Criterion compares the expected values of the other options. However, due to simplifications and assumptions, these methods are limited to relatively simple problems with low complexity. This is because they lack the possibility to assess risk, qualitative inputs and heterogenous probabilities for different outcomes.

For more complex problems, probabilistic simulation methods like the Monte Carlo Simulation and approaches like the Sensitivity Analysis can be used while also requiring more effort to conduct. However, they can also be used to support and analyze the classical approaches. In this article, the Laplace Criterion will be examined using a Monte Carlo Simulation and the critical Optimism Parameter of the Hurwicz Criterion is determined using a Sensitivity Analysis.

All these approaches can be used within Project, Program and Portfolio Management, for example, to compare two offers for outsourcing contracts within Project Management, which is illustrated later in this article. Different results are obtained depending on the decision-making approaches, which illustrates their respective focus and susceptibility to outliers.

The Decision-Making Process

Figure 1: Overview of the Decision-Making Process (based on Shaltry, 2009^[1])

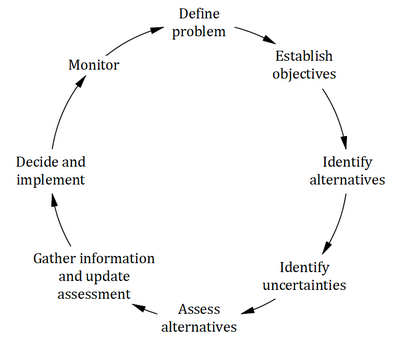
In order to reach a sensible decision for a specific problem, certain steps need to be followed (as seen in Figure 1):

Step 1: Define the problem: Specify the problem framework with the individual requirements regarding costs, time horizon, etc. It is essential to reflect which criterion should exactly be examined. This could be, for example, the cost, profit, payback or Return on Investment. If non-economic issues want to be compared, methods to quantify those aspects, such as scoring systems, should be used. ^[2]
Step 2: Establish the objectives: Describe the objectives for the given problem to create a basis to compare later alternatives depending on their degree of fulfillment and performance.
Step 3: Identify alternatives: Work out possible alternatives to satisfy the objectives and narrow them down to a shortlist that can be examined under reasonable effort later.
Step 4: Identify uncertainties: Elaborate possible scenarios that can influence the utility or cost of alternatives and connect them to the other options with their respective values.
Step 5: Assess alternatives: Conduct research or apply decision-making tools to determine which option satisfies the given objectives best.
Step 6: Gather information and update the assessment: Gather data to verify if the preferred alternative from Step 5 is actually the best alternative of all the available ones. In case crucial data was overlooked, repeat Step 5.
Step 7: Decide and implement: Make a final decision regarding which alternative to choose and assign tasks and responsibilities to it.
Step 8: Monitor: Continuously track the progress of the implementation to plan adjustments if necessary. ^[1]

Within the scope of this article, steps 5, 6 and 7 will be examined in further detail.

Differences between Decision-Making under uncertainty and risk

While decision-making under risk implies a certain probability for each possible outcome, decision-making under uncertainty assumes that these probabilities are unknown, and thus, each scenario is considered equally important. This subsequently leads to a higher inaccuracy of uncertainty problems than risk problems. An example of that would be a problem with three possible outcomes: best case, most probable case and worst case. While for decision-making under risk, both extreme scenarios would be considered with a presumable low probability and thus a low weight, for decision-making under uncertainty, all of the outcomes would be regarded in the same way, which means that case outliers have a considerably higher impact on the decision. ^[3]

Decision-Making Approaches

Various approaches can be used for decision-making. In the following, five classical strategies will be presented that can be used for problems with low complexity or for decision-support for major issues. After that, two more powerful yet elaborate methods will be introduced to show how to tackle more complex decision problems. To facilitate the understanding of the following approaches, the concept of a decision problem will be defined theoretically:

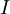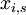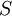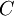A number of $I$ different decisions is available with outcomes $x_{i,s}$ for $S$ scenarios each. The data for a problem can be either given as benefits $B$ or costs $C$ . This means that the decision-maker wants to either maximize the benefit or minimize the costs, depending on the context. The following table shows the basic pattern of such a decision.

	$s_1$	$s_2$	...	$s_S$
$i_1$	$x_{1,1}$	$x_{1,2}$	...	$x_{1,S}$
$i_2$	$x_{2,1}$	$x_{2,2}$	...	$x_{2,S}$
...	...	...	...	...
$i_I$	$x_{I,1}$	$x_{I,2}$	...	$x_{I,S}$

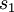
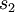
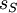
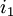
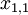
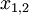
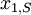
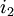
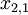
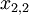
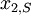
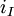
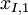
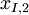
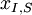
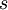The notation for the minimum and maximum values per decision alternative $i$ or scenario $s$ is the following:

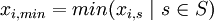
Minimum value per decision alternative: $x_{i,min} = min(x_{i,s}~|~s \in S)$
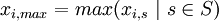
Maximum value per decision alternative: $x_{i,max} = max(x_{i,s}~|~s \in S)$
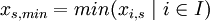
Minimum value per scenario : $x_{s,min} = min(x_{i,s}~|~i \in I)$
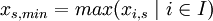Maximum value per scenario : $x_{s,min} = max(x_{i,s}~|~i \in I)$ ^[4]

Minimax Criterion

The Minimax Criterion (also called Maximin Criterion) shows a pessimistic conception: Thus, only the worst possible outcome of each alternative is considered and compared with the others. This means that all of the outcomes for the remaining scenarios remain unconsidered. It is a conservative strategy and promises the lowest assured cost (or the highest assured benefit) while neglecting possible higher gains for other outcomes. The optimal benefit or cost, respectively, according to the Minimax Criterion, is thus:

$Minimax_B = max(x_{i,min}~|~i \in I)$
$Minimax_C = min(x_{i,max}~|~i \in I)$ ^[5] ^[6]

Maximax Criterion

The Maximax Criterion (also called Minimin Criterion) works opposite to the Minimax approach: Here, the best possible outcome is considered, which means that all other outcomes are ignored. Therefore, it selects an alternative based on the maximum benefit possible (or the minimum cost possible) while disregarding more negative consequences for decision alternatives:

$B:Maximax(i) = max(x_{i,max}~|~i \in I)$
$C:Maximax(i) = min(x_{i,min}~|~i \in I)$ ^[5]

Hurwicz Criterion

The Hurwicz Criterion acts as a combination of the Minimax and the Maximax Criterion. Depending on the Optimism Parameter 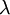$\lambda$ this approach can represent a rather optimistic or pessimistic attitude towards the outcomes of the examined alternatives. As extremes, 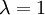$\lambda = 1$ would correspond to the Maximax Criterion and 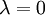$\lambda = 0$ to the Minimax Criterion. Thus, this approach allows the decision maker to find a balance between the Maximax and Minimax approach, depending on their willingness to take risks:

$Hurwicz_B = max(\lambda \times x_{i,max} + (1 - \lambda) \times x_{i,min}~|~i \in I)$
$Hurwicz_C = min(\lambda \times x_{i,min} + (1 - \lambda) \times x_{i,max}~|~i \in I)$ ^[5] ^[7]

Minimax Regret Criterion

The Minimax Regret Criterion minimizes the total opportunity costs by selecting one alternative. Opportunity costs are expressed in the missed utility that another better option could have yielded and thus represent the regret that a decision maker would have when making this decision. Therefore, every outcome is considered for each scenario and compared to the outcome for a specific alternative to find the respective opportunity costs:

$Minimax~Regret_B = max(\sum_{s=1}^{S}( x_{s,min} - x_{i,s})~|~i \in I)$
$Minimax~Regret_C = min(\sum_{s=1}^{S}( x_{s,max} - x_{i,s})~|~i \in I)$ ^[5] ^[4]

Laplace Criterion

The Laplace Criterion (also called Equal Likelihood Criterion) compares the expected value of each alternative with each other. Thereby, every outcome is considered, which means that outliers that would act as extreme values for the Minimax or Maximax Criterion will have a considerably lower importance with the Laplace Criterion. Furthermore, since there will be no consideration of only minimum or maximum values, the formula for the criterion per alternative is the same for both benefits and costs, while for benefits, the maximum and for costs, the minimum value is considered:

$Laplace_B = max((\sum_{s=1}^{S} x_{i,s})/S ~|~ i \in I)$
$Laplace_C = min((\sum_{s=1}^{S} x_{i,s})/S ~|~ i \in I)$ ^[5]

Monte Carlo Simulation

A Monte Carlo Simulation is a probabilistic simulation method used to model randomness in certain parameters to analyze how results change depending on these parameters. It is a very versatile tool and can provide valuable insights even for problems with high complexity. It is usually run a high number of times to generate multiple values to obtain a more precise end result and minimize statistical deviations. ^[8] The end result can then be either illustrated in a histogram, or box plot or analyzed further by determining statistical parameters such as the mean, variance, skewness or kurtosis. With regard to decision-making problems, the Monte Carlo Simulation can be used to model the occurrence of a scenario. Since it is assumed that all scenarios are equally probable, a decision-making basis can be the mean outcome for each alternative after generating a random scenario for a defined number of times using a Monte Carlo Simulation. Another application of the Monte Carlo Simulation is modelling a deviation of the outcome values 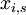$x_{i,s}$ . This can be either an absolute or relative deviation and it can even be combined with the first concept. In this way, the user can get a better understanding about the influence of different parameters and the consequences of choosing a certain alternative. ^[9]

Sensitivity Analysis

The Sensitivity Analysis examines the outputs of a problem depending on its respective inputs. It is used to model uncertainty to get an overview of how the alteration of certain variables influences the result. Concerning decision-making, a similar approach to the Monte Carlo Simulation can be pursued. The probability of certain scenarios can be increased, which decreases the probability of the remaining scenarios. Then, the result of reaching a decision based on the classical approaches could be analyzed. Moreover, the value of the outcomes 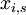$x_{i,s}$ can be altered in defined intervals to observe the subsequent result. Both of these strategies can also be applied simultaneously to display the correlation in a 3-dimensional scatter plot. In contrast to the Monte Carlo Simulation, the values for these alterations are pre-defined instead of being generated randomly. ^[10]

Application to outsourcing contracts within Project Management

The presented approaches can also be applied to Project, Program and Portfolio Management. However, since they assume that the given data is certain per scenario and can be expressed as a number, the range of sensible applications decreases. One example of utilizing these approaches is choosing suppliers for outsourcing. ^[11]

Consider the following example to see how the different methods influence the decision of which supplier to select: For a software project, parts of the front-end development are outsourced to a third-party supplier, which needs to be chosen according to their costs. Since mostly, the supplier and customer agree on a quotation with a cost estimate, the resulting costs can be higher or lower than the estimate, depending on incidents during the projects like delays, reworking or other unplanned expenses. Of course, some additional costs are already included in the cost estimate to grant the supplier a buffer. This example will consider the following 5 scenarios:

Scenario 1: None of the predicted additional costs actually occurred (best case)
Scenario 2: The actual costs are lower than the estimated costs but not as low as in scenario 1 (second-best case)
Scenario 3: The actual costs match the estimated costs (most probable case)
Scenario 4: The actual costs are higher than the estimated costs but not as high as for scenario 5 (second-worst case)
Scenario 5: On top of the estimated costs, a high number of unexpected costs occurs, which increases the overall costs drastically (worst case)

The following three suppliers can be chosen: supplier A guarantees a fixed price of 100 monetary units, no matter which scenario (i.e. how many unexpected costs will occur). Suppliers B and C, however, propose an estimated price of 100 monetary units. The actual price can vary depending on the scenario, which the following table illustrates:

Suppliers	S1	S2	S3	S4	S5
Supplier A	100	100	100	100	100
Supplier B	80	95	100	105	150
Supplier C	90	95	100	110	115

In order to determine which supplier to choose, the previously described approaches will be applied:

Beginning with the Minimax Criterion, the costs for scenario 5 are compared. It becomes clear that since supplier A offers their service for a cost matching the estimated cost, it will also provide the lowest cost in the worst-case scenario. Thus, supplier A would be picked for this approach. The Minimax Criterion can therefore be used if the project manager wants to set a lower bound for a decision that should not be exceeded. This can be the case for projects with heavy investments or tight deadlines which must be met, albeit with additional costs to speed up the processes.

For the Maximax Criterion, the costs for scenario 1 are taken into account. Supplier B as the tenderer with the highest price deviations, shows the lowest costs for the best-case scenario, which is why this supplier would be selected in this case. The fact that the costs for supplier A don't change with the scenarios shows the opposite effect to the Minimax Criterion: Since there are also no deviations towards lower prices, this supplier will not be the most attractive in case the best possible outcome occurs. The Maximax criterion can hence be used if the decision's impact is minor and taking a higher risk can be afforded.

Figure 2: Sensitivity Analysis to determine the critical Optimism Parameter for the Hurwicz Criterion

The Hurwicz Criterion represents a tendency towards the Minimax or the Maximax Criterion, depending on the Optimism Parameter λ. To find out how the risk attitude of the project manager affects the supplier decision, a sensitivity analysis will be conducted: λ is, in this case, the parameter that is modified to observe how the result changes accordingly. ^[12] The value for each supplier can be represented as a linear function:

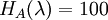
$H_A(\lambda) = 100$
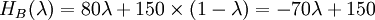
$H_B(\lambda) = 80 \lambda + 150 \times (1 - \lambda) = -70 \lambda + 150$
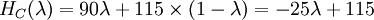
$H_C(\lambda) = 90 \lambda + 115 \times (1 - \lambda) = -25 \lambda + 115$

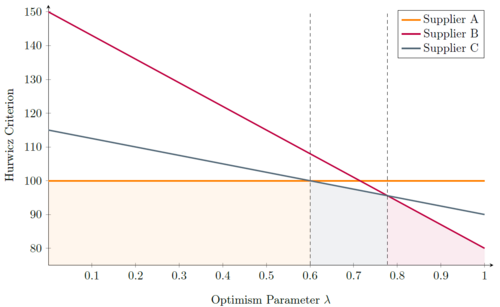
To find the critical values for the Optimism Parameter, the intersections of these 3 functions have to be determined. Equating the functions leads to the following values for λ:

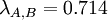
$\lambda _{A,B} = 0.714$
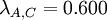
$\lambda _{A,C} = 0.600$
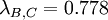
$\lambda _{B,C} = 0.778$

Figure 2 shows a graphical representation of these functions. It can be seen that there are three sections in the diagram depending on the value of λ. From the Minimax approach (λ=0) until the intersection of the function for supplier A and C supplier A will be chosen since it shows the lowest value in this region. After that, supplier C becomes more attractive and will thus be chosen. However, after the intersection between the functions for supplier B and C, it is superseded by supplier B, with supplier B staying the most attractive option until the Maxmimax approach (λ=1). While it was already evident after the Minimax and the Maximax approach, how the project manager would decide in the extreme cases (λ=0 and λ=1), a new insight could be gained by examining the Hurwicz criterion using a Sensitivity Analysis: Picking supplier C can also be an option if the Optimism parameter lies between 0.600 and 0.778, which indicates a required above-average risk attitude by the project manager.

After considering the Hurwicz Criterion, the following approach will determine the optimal alternative according to the Minimax Regret principle: Since there are no parameters to alter like the Optimism Parameter before, the result can directly be calculated. Supplier A will be chosen in this case since it has the lowest opportunity costs (which means the highest opportunity income), followed by Supplier C and then B as seen in the following table. This approach is an extension of the basic Minimax Criterion since it compares the alternatives with each other for each scenario instead of for only one outcome. Thus, it should be used for decisions where the risk of unexpected increased costs should be kept low.

Suppliers	S1	S2	S4	S5	Σ
Supplier A	20	5	0	0	25
Supplier B	0	0	5	50	55
Supplier C	10	0	10	15	35

Figure 3: Histogram for a Monte Carlo Simulation for supplier selection

Lastly, the Laplace Criterion will be calculated. Calculating the expected values for the suppliers yields the lowest cost for supplier A, followed by supplier B and finally C. However, this average value does not give an overview of the distribution of the possible outcomes, which can be additional information helping the project manager to make a decision. For example, two alternatives could have the same value for the Laplace criterion with one one featuring a broad distribution, while the values for the outcomes of the other alternative lie closer together. In order to display the distribution for the supplier selection, a Monte Carlo Simulation will be conducted. ^[13]

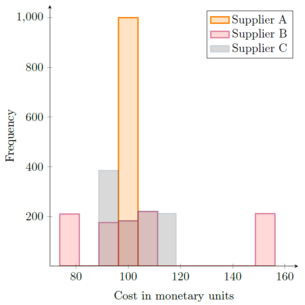
Since the scenario that will occur is uncertain, it can be modelled by generating random numbers. In this case, a random number from 1 to 5 was produced and then attributed to the respective costs for each supplier for the scenario matching the random number. This Simulation was run 1,000 times to ensure a comparably stable result. The results are illustrated in a histogram in Figure 3.

Since supplier A shows no deviation depending on the scenario, all 1,000 results yielded a cost of 100 monetary units. Comparing suppliers B and C makes clear that supplier B shows a wide spread around the estimated costs, while supplier C stays closer to the average. The reason that supplier C shows a comparably high occurence of cases with a cost between 88.75 and 96.25 is that both scenarios 1 and 2 fall into this range. Another insightful piece of information can be the comparison of the average values for the Monte Carlo Analysis per supplier with the respective Laplace Criteria, which the following table shows:

Issue examined	Supplier A	Supplier B	Supplier C
Laplace Criterion	100.00	106.00	102.00
Monte Carlo Sim.	100.00	106.58	102.40
Deviation	0.00 %	0.55 %	0.39 %

It is noticeable that for 1,000 simulated values, the deviations are minuscule, and calculating the mean value results in the same result as the Laplace approach. Considering the simulated distribution together with this finding, the project manager should pick supplier A due to lower average costs and the narrowest distribution. This procedure provides both an overview of the mean costs of decision alternatives as well as of the respective distributions and can thus be used to get a better understanding of how the scenarios affect the individual outcomes.

A point that can be criticized is that only the costs were considered in this example and not features like reliability or service quality. Also, all the outcomes were assumed to have an equal probability of happening, which is rather unrealistic. Especially considering scenario 5 equally probable put a high weight on the 150 monetary units of supplier B for this scenario. However, for minor supplier selection decisions, these approaches provide results with low effort. Concluding this section, the selection of the approach for a problem depends on the risk the project manager wants to take and the information they are trying to extract. In order to get a better understanding of the consequences of a selection, performing different approaches and comparing their results is recommended to make a decision. ^[3]

Limitations

While the described approaches can be applied in practice for different use cases in Project, Program and Portfolio Management, they also have their limitations: First of all, the assumption that the given data is reliable can be criticized. Since scenarios with certain outcomes are mostly developed based on conjectures rather than on facts, they always bring along inaccuracies. Secondly, the fact that every scenario is considered equally likely can cause distortions regarding extreme cases. For example, the worst- and the best-case scenario are usually less probable compared to a scenario with an outcome closer to the expected value. If the probabilities were known, tools for decision-making under risk could be applied to obtain a more accurate result. Another point of criticism is that with the classical approaches, only one criterion can be examined at a time. To compare multiple features like costs together with duration, the criteria can be assigned a percentage weight before applying the strategies to all the criteria and calculating the weighted result to determine a preferred alternative. However, this procedure comes with even more inaccuracy since setting a weight between different features comes with subjectivity. ^[4] However, to provide a quantitative foundation for decision-making, these approaches are very useful and considering the required effort fairly easy to implement. ^[14]

Annotated bibliography

Shaltry, P. E. (2009). The Project Manager’s Guide to Making Successful Decisions. Project Management Journal, 40(4).

The book covers the basic principles and procedures of decision-making within Project Management and shows approaches on how to make a decision considering different project life cycle phases. Aside from uncertainty, it also deals with decision-making under risk which can be used when the probabilities of scenarios are known. Another aspect this book introduces is framing within decision-making. That means that depending on the context of the problem, a decision-making strategy can yield different results.

Chung ES, Kim Y. Development of fuzzy multi-criteria approach to prioritize locations of treated wastewater use considering climate change scenarios. J Environ Manage. 2014 Dec 15;146:505-516.

This research paper shows a concept of how to prioritize treated wastewater locations with data containing different climate change scenarios. As a case study, ten concepts for prioritizing locations for a Korean urban watershed were evaluated using the Minimax, Maximax, Hurwicz, Minimax Regret, and Laplace Criterion. Comparing the results for the different approaches provides further insights into how these strategies deal with outliers and uneven data distribution.

Brandimarte, P. (2014). Handbook in Monte Carlo simulation: Applications in financial engineering, risk management, and economics. Wiley-Blackwell.

This book describes the Monte Carlo simulation from a theoretical point of view before illustrating various applications within finance and risk management. It provides deeper insights regarding problem modelling, integration of the strategy and analyses of results.

References

↑ ^1.0 ^1.1 Shaltry, P. E. (2009). The Project Manager’s Guide to Making Successful Decisions. Project Management Journal, 40(4).
↑ Züst, R., & Troxler, P. (2006). No More Muddling Through. Springer Netherlands. https://doi.org/10.1007/978-1-4020-5018-3
↑ ^3.0 ^3.1 Kerzner, H. R. (2017). Project management: A systems approach to planning, scheduling, and controlling (12th ed.). John Wiley & Sons.
↑ ^4.0 ^4.1 ^4.2 Renou, L., & Schlag, K. H. (2010). Minimax regret and strategic uncertainty. In Journal of Economic Theory (Vol. 145, Issue 1, pp. 264–286). Elsevier BV. https://doi.org/10.1016/j.jet.2009.07.005
↑ ^5.0 ^5.1 ^5.2 ^5.3 ^5.4 Chung ES, Kim Y. Development of fuzzy multi-criteria approach to prioritize locations of treated wastewater use considering climate change scenarios. J Environ Manage. 2014 Dec 15;146:505-516. doi: 10.1016/j.jenvman.2014.08.013.
↑ Maclean, F. I. (1987). Rectangular game theory and metabolic response to random changes in environmental states. In Biosystems (Vol. 20, Issue 3, pp. 259–266). Elsevier BV. https://doi.org/10.1016/0303-2647(87)90033-5
↑ Geronymakis, P., Troullinos, D., Chalkiadakis, G., & Papageorgiou, M. (2022). Collaborative Decision Making for Lane-Free Autonomous Driving in the Presence of Uncertainty. In Multi-Agent Systems (pp. 171–187). Springer International Publishing. https://doi.org/10.1007/978-3-031-20614-6_10
↑ Brandimarte, P. (2014). Handbook in Monte Carlo simulation: Applications in financial engineering, risk management, and economics. Wiley-Blackwell. https://doi.org/10.1002/9781118593264
↑ Raychaudhuri, S. (2008, December). Introduction to monte carlo simulation. In 2008 Winter simulation conference (pp. 91-100). IEEE.
↑ Iooss, B., & Saltelli, A. (2017). Introduction to Sensitivity Analysis. In Handbook of Uncertainty Quantification (pp. 1103–1122). Springer International Publishing. https://doi.org/10.1007/978-3-319-12385-1_31
↑ Bennett, N., & Axelos. (2017). Managing successful projects with PRINCE2 (The Stationery Office, Ed.; 6th ed.). TSO.
↑ Jiang, Z.-Z., Zhang, R., Fan, Z.-P., & Chen, X. (2014). A fuzzy matching model with Hurwicz criteria for one-shot multi-attribute exchanges in E-brokerage. In Fuzzy Optimization and Decision Making (Vol. 14, Issue 1, pp. 77–96). Springer Science and Business Media LLC. https://doi.org/10.1007/s10700-014-9189-x
↑ Fang, W., Wang, Z., Giles, M. B., Jackson, C. H., Welton, N. J., Andrieu, C., & Thom, H. (2021). Multilevel and Quasi Monte Carlo Methods for the Calculation of the Expected Value of Partial Perfect Information. In Medical Decision Making (Vol. 42, Issue 2, pp. 168–181). SAGE Publications. https://doi.org/10.1177/0272989x211026305
↑ Mohanty, S. N., & Suar, D. (2014). Decision Making under Uncertainty and Information Processing in Positive and Negative Mood States. In Psychological Reports (Vol. 115, Issue 1, pp. 91–105). SAGE Publications. https://doi.org/10.2466/20.04.pr0.115c16z2

[Shaltry2009-0] 1.0 ^1.1 Shaltry, P. E. (2009). The Project Manager’s Guide to Making Successful Decisions. Project Management Journal, 40(4).

[Z.C3.BCst2006-1] Züst, R., & Troxler, P. (2006). No More Muddling Through. Springer Netherlands. https://doi.org/10.1007/978-1-4020-5018-3

[Kerzner2017-2] 3.0 ^3.1 Kerzner, H. R. (2017). Project management: A systems approach to planning, scheduling, and controlling (12th ed.). John Wiley & Sons.

[Renou2010-3] 4.0 ^4.1 ^4.2 Renou, L., & Schlag, K. H. (2010). Minimax regret and strategic uncertainty. In Journal of Economic Theory (Vol. 145, Issue 1, pp. 264–286). Elsevier BV. https://doi.org/10.1016/j.jet.2009.07.005

[Chung2014-4] 5.0 ^5.1 ^5.2 ^5.3 ^5.4 Chung ES, Kim Y. Development of fuzzy multi-criteria approach to prioritize locations of treated wastewater use considering climate change scenarios. J Environ Manage. 2014 Dec 15;146:505-516. doi: 10.1016/j.jenvman.2014.08.013.

[Maclean1987-5] Maclean, F. I. (1987). Rectangular game theory and metabolic response to random changes in environmental states. In Biosystems (Vol. 20, Issue 3, pp. 259–266). Elsevier BV. https://doi.org/10.1016/0303-2647(87)90033-5

[Geronymakis2022-6] Geronymakis, P., Troullinos, D., Chalkiadakis, G., & Papageorgiou, M. (2022). Collaborative Decision Making for Lane-Free Autonomous Driving in the Presence of Uncertainty. In Multi-Agent Systems (pp. 171–187). Springer International Publishing. https://doi.org/10.1007/978-3-031-20614-6_10

[Brandimarte2014-7] Brandimarte, P. (2014). Handbook in Monte Carlo simulation: Applications in financial engineering, risk management, and economics. Wiley-Blackwell. https://doi.org/10.1002/9781118593264

[Raychaudhuri2008-8] Raychaudhuri, S. (2008, December). Introduction to monte carlo simulation. In 2008 Winter simulation conference (pp. 91-100). IEEE.

[Iooss2017-9] Iooss, B., & Saltelli, A. (2017). Introduction to Sensitivity Analysis. In Handbook of Uncertainty Quantification (pp. 1103–1122). Springer International Publishing. https://doi.org/10.1007/978-3-319-12385-1_31

[Bennett2017-10] Bennett, N., & Axelos. (2017). Managing successful projects with PRINCE2 (The Stationery Office, Ed.; 6th ed.). TSO.

[Jiang2014-11] Jiang, Z.-Z., Zhang, R., Fan, Z.-P., & Chen, X. (2014). A fuzzy matching model with Hurwicz criteria for one-shot multi-attribute exchanges in E-brokerage. In Fuzzy Optimization and Decision Making (Vol. 14, Issue 1, pp. 77–96). Springer Science and Business Media LLC. https://doi.org/10.1007/s10700-014-9189-x

[Fang2021-12] Fang, W., Wang, Z., Giles, M. B., Jackson, C. H., Welton, N. J., Andrieu, C., & Thom, H. (2021). Multilevel and Quasi Monte Carlo Methods for the Calculation of the Expected Value of Partial Perfect Information. In Medical Decision Making (Vol. 42, Issue 2, pp. 168–181). SAGE Publications. https://doi.org/10.1177/0272989x211026305

[Mohanty2014-13] Mohanty, S. N., & Suar, D. (2014). Decision Making under Uncertainty and Information Processing in Positive and Negative Mood States. In Psychological Reports (Vol. 115, Issue 1, pp. 91–105). SAGE Publications. https://doi.org/10.2466/20.04.pr0.115c16z2

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

@@ Line 104: / Line 104: @@
 ====Monte Carlo Simulation====
-A Monte Carlo Simulation is a probabilistic simulation method used to model randomness in certain parameters to analyze how results change depending on these parameters. It is a very versatile tool and can provide valuable insights even for problems with high complexity. It is usually run a high number of times to generate multiple values to obtain a more precise end result and minimize statistical deviations. <ref name="Brandimarte2014"/> The end result can then be either illustrated in a histogram, or box plot or analyzed further by determining statistical parameters such as the mean, variance, scewness or kurtosis. With regard to decision-making problems, the Monte Carlo Simulation can be used to model the occurrence of a scenario. Since it is assumed that all scenarios are equally probable, a decision-making basis can be the mean outcome for each alternative after generating a random scenario for a defined number of times using a Monte Carlo Simulation. Another application of the Monte Carlo Simulation is modelling a deviation of the outcome values <math>x_{i,s}</math>. This can be either an absolute or relative deviation and it can even be combined with the first concept. In this way, the user can get a better understanding about the influence of different parameters and the consequences of choosing a certain alternative. <ref name="Raychaudhuri2008"/>
+A Monte Carlo Simulation is a probabilistic simulation method used to model randomness in certain parameters to analyze how results change depending on these parameters. It is a very versatile tool and can provide valuable insights even for problems with high complexity. It is usually run a high number of times to generate multiple values to obtain a more precise end result and minimize statistical deviations. <ref name="Brandimarte2014"/> The end result can then be either illustrated in a histogram, or box plot or analyzed further by determining statistical parameters such as the mean, variance, skewness or kurtosis. With regard to decision-making problems, the Monte Carlo Simulation can be used to model the occurrence of a scenario. Since it is assumed that all scenarios are equally probable, a decision-making basis can be the mean outcome for each alternative after generating a random scenario for a defined number of times using a Monte Carlo Simulation. Another application of the Monte Carlo Simulation is modelling a deviation of the outcome values <math>x_{i,s}</math>. This can be either an absolute or relative deviation and it can even be combined with the first concept. In this way, the user can get a better understanding about the influence of different parameters and the consequences of choosing a certain alternative. <ref name="Raychaudhuri2008"/>
 ====Sensitivity Analysis====

Data-Driven Decision-Making under Uncertainty

Revision as of 17:51, 9 May 2023

Contents

The Decision-Making Process

Differences between Decision-Making under uncertainty and risk

Decision-Making Approaches

Minimax Criterion

Maximax Criterion

Hurwicz Criterion

Minimax Regret Criterion

Laplace Criterion

Monte Carlo Simulation

Sensitivity Analysis

Application to outsourcing contracts within Project Management

Limitations

Annotated bibliography

References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox