MCDM-APH method in decision making
(→Preform consistancy test) |
(→Preform consistancy test) |
||
| Line 216: | Line 216: | ||
<math>CI =\[\frac{\lambda_{max} - n}{n-1}\]</math> | <math>CI =\[\frac{\lambda_{max} - n}{n-1}\]</math> | ||
| − | <math> | + | <math>\frac{1}{2}\</math> |
===Calculate the global priority of each criteria and ranking=== | ===Calculate the global priority of each criteria and ranking=== | ||
Revision as of 22:16, 18 February 2023
The MCDM-APH (Multi-Criteria Decision Making - Analytic Hierarchy Process) is a tool that makes complex decisions. MCDM is a systematic approach that evaluate conflicting criterias in decision making, one of these approaches is APH which uses a mathematic method to derive a relative importance of criteria in a decision problem.
The method was developed in the 1970s by Thomas Saaty [1], AHP is a mathematical method that is used to derive the relative importance of criteria in a decision problem. The idea behind the method is that a decision problem can be represented as a hierarchical structure, with the most important criteria at the top followed by the lesser important criteria at the bottom.
Decision-making is at the core of project management and yet it can be a daunting task, especially when the projects are complex and multi-facted projects. The pressure of making decisions in a timely and informed manner can be compounded when the criteria for success is not defined clearly, At time like this it not unusual that project managers may feel overwhelmed and unable to determine the most important factors to consider. This is where the APH-decision-making method provides a systematic approach to this challenge. This approach is addressing the complexity of decision making by Segmenting the process into manageable chunks. By following these steps the project manager can get a obtain a holistic view of the project's key performance indicators and success factors.
Contents |
Project selection
The analytic hierarchy process
Assuming that we have multiple criterias and alternatives, the weight of the criterias is first weighted using pairwise comparison, using saatys scale:
| Fundamental scale | ||
|---|---|---|
| Intensity of importance | Definition | Explanation |
| 1 | Equal importance | Two activities contribute equally to the objective |
| 2 | Weak or slightly | |
| 3 | Moderate importance | Experience and judgment slightly favor one activity over another |
| 4 | Moderate plus | |
| 5 | Strong importance | Experience and judgment strongly favor one activity over another |
| 6 | Strong plus | |
| 7 | Very strong | An activity is favored very strongly over another, its dominance demonstrated in practice |
| 8 | Very, very strong | |
| 9 | Extreme importance | The evidence favoring one activity over another is of the highest possible order of affirmation |
| Table 1: Saatys scale [2] | ||
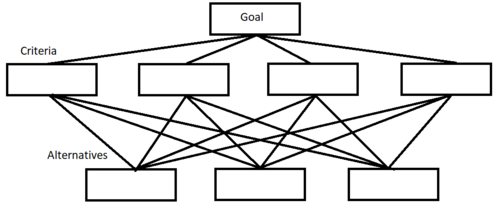
The APH method makes use of the hiracy approach, where the objective is at the top and criteria is below it and the alternatives are at the bottom.
Example for AHP
- Identify the objectives
- Assign weights to the criteria by performing pairwise comparisons
- Evaluate the performance of each alternative with respect to each criterion
- Preform Consistancy test
- Calculate the global priority of each criteria and ranking
Idenrify the objective
A company is in the process of implementing a PMO system and is considering 3 providors. The company have come up with three specific criteria, which are considered highly important when determining which product they should buy. These criteria are cost, technical support, and flexibility.
Assign weights to the criteria by performing pairwise comparisons
When the objective is identified and relevent emperical information is gathered, the next step is to determin the relative importance among the criteria that is under consideration. This process involves giving a specific weight to each criteria based on its percieved importance. This step establish a hierachy, it ensures that the most significant criteria is given appropriate attention. This is done by giving each criteria a relative importance in the Saatys scale 1-9 as shown in table 1, which a person decides. It should be noted that the sum of each row is computed, this is used for later calculations.
| Cost | Support | Flexibility | |
|---|---|---|---|
| Cost | 1,00 | 2,00 | 3,00 |
| Support | 0,50 | 1,00 | 2,00 |
| Flexibility | 0,33 | 0,50 | 1,00 |
| Sum | 1,83 | 3,50 | 6,00 |
Evaluate the performance of each alternative with respect to each criterion
The alternatives are assesed by making a pariwise comparision, just like the previous step. For this step the alternatives are compared against eachother with respect to each criterion the, where they are given a relative importance just like earlier, which a person decides. they are then compiled into tabels, shown below:
| Alternatives with respect to cost | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 7,00 | 2,00 |
| Company 2 | 0,14 | 1,00 | 0,25 |
| Company 3 | 0,50 | 4,00 | 1,00 |
| sum | 1,64 | 12,00 | 3,25 |
| Alternatives with respect to support | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 5,00 | 3,00 |
| Company 2 | 0,20 | 1,00 | 0,50 |
| Company 3 | 0,33 | 2,00 | 1,00 |
| Sum | 1,53 | 8,00 | 4,50 |
| Alternatives with respect to flexibility | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 1,00 | 1,00 |
| Company 2 | 1,00 | 1,00 | 1,00 |
| Company 3 | 1,00 | 1,00 | 1,00 |
| Sum | 3,00 | 3,00 | 3,00 |
Preform consistancy test
When preforming the consistancy the following is computed:
- The largest eigenvalue, λ_max, of the matrix is calculated
- The Consistency index (CI) and the consistency ratio (CR) is calculated
Math software, like maple, was used to find the largest eigenvalue of the matrix. The consistency index is calculated with the following formula:
Failed to parse (unknown error): CI =\[\frac{\lambda_{max} - n}{n-1}\]
Failed to parse (unknown error): \frac{1}{2}\
Calculate the global priority of each criteria and ranking
Critique of the AHP method
Inplementation of AHP method in organisations
References
- ↑ Saaty, T. L. How to make a decision: The analytic hierarchy process. European Journal of Operational Research, 48(1), 9-26, 1990. https://www.sciencedirect.com/science/article/pii/037722179090057I
- ↑ Saaty, Int. J. Services Sciences, Vol. 1, No. 1, 2008 https://www.rafikulislam.com/uploads/resourses/197245512559a37aadea6d.pdf