Decision tree analysis
| Line 31: | Line 31: | ||
*'''Branches:''' The branches in a decision tree model represent chance outcomes or occurrences that arise from root nodes and internal nodes. Decision trees are constructed by organizing branches into a hierarchy. Each path from the root node through internal nodes to a leaf node represents a classification decision rule, which can also be expressed as an "if-then" statement. For instance, "if condition 1 and condition 2 and condition...and condition k occur, then outcome j occurs." | *'''Branches:''' The branches in a decision tree model represent chance outcomes or occurrences that arise from root nodes and internal nodes. Decision trees are constructed by organizing branches into a hierarchy. Each path from the root node through internal nodes to a leaf node represents a classification decision rule, which can also be expressed as an "if-then" statement. For instance, "if condition 1 and condition 2 and condition...and condition k occur, then outcome j occurs." | ||
| − | *'''Splitting:''' This involves using only input variables related to the target variable to divide parent nodes into more child nodes of the same kind. This can be done using both discrete and continuous input variables, which are collapsed into two or more categories. To begin this process, the most important input variables must first be identified. Then, the records at the root node and subsequent internal nodes are split into two or more categories or "bins" based on the status of these variables. | + | *'''Splitting:''' This involves using only input variables related to the target variable to divide parent nodes into more child nodes of the same kind. This can be done using both discrete and continuous input variables, which are collapsed into two or more categories. To begin this process, the most important input variables must first be identified. Then, the records at the root node and subsequent internal nodes are split into two or more categories or "bins" based on the status of these variables. This splitting process continues until predetermined homogeneity or stopping criteria are met. It's worth noting that not all potential input variables may be used in building the decision tree model, and sometimes a specific input variable may be used multiple times at different levels of the decision tree. |
| − | This splitting process continues until predetermined homogeneity or stopping criteria are met. It's worth noting that not all potential input variables may be used in building the decision tree model, and sometimes a specific input variable may be used multiple times at different levels of the decision tree. | + | |
*'''Stopping:''' Complexity and robustness are two key factors to consider when building a statistical model, especially when developing a decision tree. The complexity of the model can negatively impact its reliability when predicting future records. For instance, a highly complex decision tree model that produces leaf nodes with 100% pure records may be overfitted to the existing observations, making it unreliable in predicting future cases. To avoid this, stopping rules should be applied when building the decision tree to prevent it from becoming too complex. Common parameters used in stopping rules include the minimum number of records in a leaf, the minimum number of records in a node before splitting, and the depth of any leaf from the root node. It's important to select stopping parameters based on the analysis goal and the dataset's characteristics. | *'''Stopping:''' Complexity and robustness are two key factors to consider when building a statistical model, especially when developing a decision tree. The complexity of the model can negatively impact its reliability when predicting future records. For instance, a highly complex decision tree model that produces leaf nodes with 100% pure records may be overfitted to the existing observations, making it unreliable in predicting future cases. To avoid this, stopping rules should be applied when building the decision tree to prevent it from becoming too complex. Common parameters used in stopping rules include the minimum number of records in a leaf, the minimum number of records in a node before splitting, and the depth of any leaf from the root node. It's important to select stopping parameters based on the analysis goal and the dataset's characteristics. | ||
| − | *'''Pruning:''' Stopping rules may not always be effective in preventing decision trees from becoming overly complex. Instead, one alternative is to grow a larger tree and then prune it to its optimal size by removing nodes that add less value.<ref name = "Hastie">Hastie T, Tibshirani R, Friedman J.The Elements of Statistical Learning. Springer; 2001. p. 269-272</ref> One way to select the best sub-tree from several candidates is to consider the proportion of records with prediction errors (i.e., the proportion in which the predicted outcome is incorrect). Alternatively, a validation dataset can be used by dividing the sample into two sets and testing the model developed on the training dataset on the validation dataset. For smaller samples, cross-validation can be used by dividing the sample into 10 groups or "folds," developing the model from nine folds, and testing it on the 10th fold, repeating the process for all ten combinations, and averaging the error rates. Pruning can be either pre-pruning (forward pruning) or post-pruning (backward pruning). Pre-pruning prevents the generation of insignificant branches by using chi-square tests [6] or multiple-comparison adjustment methods. Post-pruning is performed after generating a full decision tree and involves removing branches in a way that improves the accuracy of the overall classification when applied to the validation dataset. | + | *'''Pruning:''' Stopping rules may not always be effective in preventing decision trees from becoming overly complex. Instead, one alternative is to grow a larger tree and then prune it to its optimal size by removing nodes that add less value.<ref name = "Hastie">Hastie T, Tibshirani R, Friedman J.The Elements of Statistical Learning. Springer; 2001. p. 269-272</ref> One way to select the best sub-tree from several candidates is to consider the proportion of records with prediction errors (i.e., the proportion in which the predicted outcome is incorrect). Alternatively, a validation dataset can be used by dividing the sample into two sets and testing the model developed on the training dataset on the validation dataset. For smaller samples, cross-validation can be used by dividing the sample into 10 groups or "folds," developing the model from nine folds, and testing it on the 10th fold, repeating the process for all ten combinations, and averaging the error rates. Pruning can be either pre-pruning (forward pruning) or post-pruning (backward pruning). Pre-pruning prevents the generation of insignificant branches by using chi-square tests [6] or multiple-comparison adjustment methods. Post-pruning is performed after generating a full decision tree and involves removing branches in a way that improves the accuracy of the overall classification when applied to the validation dataset. <ref name = "Song">Song YY, Lu Y. Decision tree methods: applications for classification and prediction. Shanghai Arch Psychiatry. 2015 Apr 25;27(2):130-5. doi: 10.11919/j.issn.1002-0829.215044. PMID: 26120265; PMCID: PMC4466856.</ref> |
| + | |||
=='''Application'''== | =='''Application'''== | ||
---- | ---- | ||
Revision as of 13:15, 8 May 2023
Contents |
Abstract
In every persons personal and professional life, they are always faced with decisions. These decisions are both small and large and can have great impact on organizations and their goals. Making the “right” decision can often be difficult, which is why numerous tools have been developed over the years to help with this. One of those tools is decision tree analysis.
Decision tree analysis is a method that uses graphical representation to show the decision-making process given certain conditions. It’s most often used to determine the optimal decision based on data and to estimate the potential consequences of a decision when faced different circumstances. The history of decision tree analysis is complex, with several mathematicians and others developing it over time. However, in the industrial environment, decision making usually involves analysing the data to reach a conclusion. Decision tree analysis has, over the years, become increasingly more used in real life, and numerous case studies show its usefulness in improving efficiency in organizations and customer satisfaction. A common use of decision tree analysis is to help with project-selection, which is a necessary part of decision-making process. A number of different instances call for the use of decision tree analysis, and the procedure has bee shown to provide important benefits in a lot of different instances. [1]
Decision tree analysis can be used in project, program, and portfolio management to help with the decision-making process in relation to project selection, prioritization as well as risk management. Decision tree analysis can assist managers and other people responsible for making decisions in determining the best course of action and effectively allocate resources by examining many scenarios and potential outcomes.
Overview
Decision trees are structures, similar to flowcharts, and are often used in decision analysis for both visual and analytical support tool. When competing options, based on their projected values, decision trees are particularly helpful. In the decision tree, there are nodes which represent different types of events or actions. Connected to the nodes are branches which represent all the possible outcomes for each event or action. In decision trees, there are typically three different types of nodes:[2]
- The decision node
- These are used to represent the decision that need to be made based on the information at hand.
- Typically represented as a square
- The chance node
- These are used to represent events that are out of control, for example a coin toss
- Typically represented as a circle
- The end node
- Used to represent the final outcome of the whole decision-making progress
- Typically represented as a triangle
Basic concepts of decision tree analysis
In decision tree analysis there are a few concepts that are used in connection to it. These concepts are:
- Nodes: Decision trees consist of three types of nodes. The first type is the root node, which is also known as the decision node. This node represents a choice that divides all records into two or more mutually exclusive subsets. The second type is internal nodes, also referred to as chance nodes. These nodes represent one of the available choices at that point in the tree structure. The top edge of the node connects it to the parent node, while the bottom edge connects it to its child nodes or leaf nodes. The third type is leaf nodes, which are also known as end nodes. These nodes represent the final result of a combination of decisions or events.
- Branches: The branches in a decision tree model represent chance outcomes or occurrences that arise from root nodes and internal nodes. Decision trees are constructed by organizing branches into a hierarchy. Each path from the root node through internal nodes to a leaf node represents a classification decision rule, which can also be expressed as an "if-then" statement. For instance, "if condition 1 and condition 2 and condition...and condition k occur, then outcome j occurs."
- Splitting: This involves using only input variables related to the target variable to divide parent nodes into more child nodes of the same kind. This can be done using both discrete and continuous input variables, which are collapsed into two or more categories. To begin this process, the most important input variables must first be identified. Then, the records at the root node and subsequent internal nodes are split into two or more categories or "bins" based on the status of these variables. This splitting process continues until predetermined homogeneity or stopping criteria are met. It's worth noting that not all potential input variables may be used in building the decision tree model, and sometimes a specific input variable may be used multiple times at different levels of the decision tree.
- Stopping: Complexity and robustness are two key factors to consider when building a statistical model, especially when developing a decision tree. The complexity of the model can negatively impact its reliability when predicting future records. For instance, a highly complex decision tree model that produces leaf nodes with 100% pure records may be overfitted to the existing observations, making it unreliable in predicting future cases. To avoid this, stopping rules should be applied when building the decision tree to prevent it from becoming too complex. Common parameters used in stopping rules include the minimum number of records in a leaf, the minimum number of records in a node before splitting, and the depth of any leaf from the root node. It's important to select stopping parameters based on the analysis goal and the dataset's characteristics.
- Pruning: Stopping rules may not always be effective in preventing decision trees from becoming overly complex. Instead, one alternative is to grow a larger tree and then prune it to its optimal size by removing nodes that add less value.[3] One way to select the best sub-tree from several candidates is to consider the proportion of records with prediction errors (i.e., the proportion in which the predicted outcome is incorrect). Alternatively, a validation dataset can be used by dividing the sample into two sets and testing the model developed on the training dataset on the validation dataset. For smaller samples, cross-validation can be used by dividing the sample into 10 groups or "folds," developing the model from nine folds, and testing it on the 10th fold, repeating the process for all ten combinations, and averaging the error rates. Pruning can be either pre-pruning (forward pruning) or post-pruning (backward pruning). Pre-pruning prevents the generation of insignificant branches by using chi-square tests [6] or multiple-comparison adjustment methods. Post-pruning is performed after generating a full decision tree and involves removing branches in a way that improves the accuracy of the overall classification when applied to the validation dataset. [4]
Application
How to create a decision tree
Creating a decision tree is fairly simple, it can be good to split the process into 5 main steps:[5]
1. What decision has to be made
Begin the decision tree analysis with one idea, or decision that has to be made. That will be the decision node and from that add branches for the different options that have to be chosen.
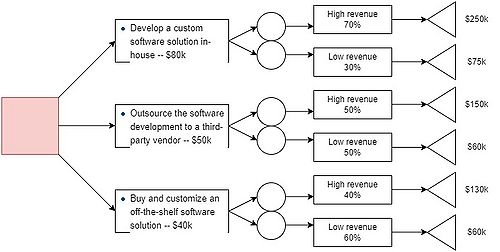
For example, if a project manager is considering three different options for a new software development project. The three different options are:
- Develop a custom software solution in-house
- Outsource the software development to a third-party vendor
- Buy and customize an off-the-shelf software solution
2. Add chance and decision nodes
After adding your main idea to the tree, continue adding chance or decision nodes after each decision to expand your tree further. A chance node may need an alternative branch after it because there could be more than one potential outcome for choosing that decision. After the initial idea, the next step is to add chance and decision nodes after every decision to expand the tree. Chance nodes might need more branches after them since there can be more than one outcome. In the example mentioned, the chance nodes could be: "Success of the project". and have two branches, one for low success and the other for high success. These nodes then can have expected revenue branches for the corresponding decisions.
3. Expand the tree until completion
To create a comprehensive decision tree, continue adding chance and decision nodes until the tree can no longer be expanded. When the tree is fully developed, add end nodes to show that the decision tree creation process is finished. With the completed decision tree, you can start analysing each of the decisions, evaluating their potential outcomes and associated risks.
4. Calculate tree values
In an ideal scenario, decision trees should have quantifiable data associated with them. The most common data used in decision trees is monetary value, where costs and expected returns are taken into consideration to make the final decision. For instance, outsourcing the software development project has different costs and profits than developing it in house. Quantifying these values under each decision can help in the decision-making process.
Moreover, it is also possible to estimate the expected value of each decision, which can be helpful in selecting the best possible outcome. Expected value is calculated based on the likelihood of each possible outcome and its associated cost. This calculation can be performed using the following formula: Expected value (EV) = (First possible outcome x Likelihood of outcome) + (Second possible outcome x Likelihood of outcome) - Cost
In order to calculate the expected value, multiply both possible outcomes by the likelihood that each outcome will occur, and then add those values. Finally, subtract any initial costs from the total value to get the expected value of each outcome. This can help to identify the most cost-effective and beneficial option among the various available choices in a decision-making process.
5. Evaluate outcomes
After calculating the expected values for each decision in the decision tree, the next step is to evaluate the level of risk option has. It is necessary to understand that the decision with the highest expected value may not necessarily be the best option. The level of risk associated with the decision should also be taken into account.
Risk is an inherent aspect in project management, and each decision has its own level of risk. Therefore, it is crucial to evaluate the risk level associated with each decision to determine if it aligns with the project's goals and objectives. If a decision has a high expected value but also comes with high project risk, it may not be the best choice for the project.
Decision trees in project management
Using decision tree analysis can be a powerful tool that project managers can use to help them make informed decisions in relation to project management. This method can add value to projects, with thorough analysis of all available options and their possible risks.
There are many ways that decision tree analysis can be used in project management, for example project selection, risk management, resource allocation and project execution.[1] Using it for project selection can involve comparing potential value for each of the options with regards to profits, costs and risks. This allows project managers to make informed decisions and select the project with the most potential to add value to their companies and organizations. An example of this is a business can use decision tree analysis to decide which project to invest in by comparing the expected profit for the different projects.
In risk management, decision tree analysis is useful to identify and assess threats at the same time, make actions to mitigate those threats. By conducting analysis of all the various risk scenarios with the use of decision trees, project managers are able to prioritize the biggest and most critical risks and develop strategies to mitigate them and increase the likelihood of a successful project. This method helps to reduce the negative impacts of risks that can affect the outcome of projects and increase the likelihood of meeting the project objectives. [6]
Another category where decision trees can be applied in project management is resource allocation. Using decision trees allows project managers to evaluate various scenarios with different resource allocation while analysing the expected value of each option as well as the risks involved. This helps project managers in allocating resources to the right places to maximize the value of projects and minimizing the risks.
Lastly, it’s possible to use decision tree analysis to compare various options of project execution. There are often different ways of executing projects, some strategies are more aggressive while others are more conservative. Decision tree analysis can be used to compare the costs involved with these strategies and the potential profits to determine which strategy is the best choice to add the most value to the project.
Application in other sectors
Numerous industries use decision tree analysis to help people make decisions from a variety of options. These applications include social, business, banking, libraries, hospitals and more. Any project or product's success depends on a number of choices made during the production process, including the selection of raw material and component vendors, equipment, workforce, sales, and marketing strategies. Decision tree analysis can offer quantitative terms to help the decision maker in instances when a choice must be made from a variety of options.
For example, decision tree analysis can be useful when there are multiple objectives that have to be considered at the same time, making it difficult for a decision maker to weigh the potential negative consequences on one element vs another. Decision tree analysis, often along with additional tools or methods, can be helpful in certain situations. In addition to direct benefits, decision makers can also acquire indirect ones by selecting the best choice, which can be done with the use of decision tree analysis. A well-informed choice can also assist organizations in attaining their long-term objectives, emphasizing the value of decision-making not just as a situational activity but also as a strategy for long-term success [1]
Limitations
Decision trees often suffer the disadvantage of excessive complexity and are therefore incomprehensible to experts.
As decision trees use the “divide and conquer” method, they tend to perform well if a few highly relevant attributes exist, but less so if many complex interactions are present. One of the reasons for this is that other classifiers can compactly describe a classifier that would be very challenging to represent using a decision tree.
The greedy characteristic of decision trees leads to another disadvantage that should be pointed out. This is its over-sensitivity to the training set, to irrelevant attributes and to noise.
References
- ↑ 1.0 1.1 1.2 1.3 Tewari, Puran & Mittal, Kapil & Khanduja, Dinesh. (2017). An Insight into “Decision Tree Analysis”. World Wide Journal of Multidisciplinary Research and Development. 3. 111-115.
- ↑ Kamiński, B., Jakubczyk, M. & Szufel, P. A framework for sensitivity analysis of decision trees. Cent Eur J Oper Res 26, 135–159 (2018). https://doi.org/10.1007/s10100-017-0479-6
- ↑ Hastie T, Tibshirani R, Friedman J.The Elements of Statistical Learning. Springer; 2001. p. 269-272
- ↑ Song YY, Lu Y. Decision tree methods: applications for classification and prediction. Shanghai Arch Psychiatry. 2015 Apr 25;27(2):130-5. doi: 10.11919/j.issn.1002-0829.215044. PMID: 26120265; PMCID: PMC4466856.
- ↑ What is decision tree analysis? 5 steps to make better decisions (2021, December 10). Asana. Retrieved from https://asana.com/resources/decision-tree-analysis. This website was used as a guide to explain how to create decision trees. The steps explained might not work for everyone.
- ↑ Prasanta Kumar Dey (2012) Project risk management using multiple criteria decision-making technique and decision tree analysis: a case study of Indian oil refinery, Production Planning & Control, 23:12, 903-921, DOI: 10.1080/09537287.2011.586379