The Critical Path Method in project planning
(→Time-Cost Trade-Off) |
(→Time-Cost Trade-Off) |
||
| Line 60: | Line 60: | ||
The cost slope in Figure x is calculated by inserting relevant values into the cost slope equation. For example, for activity C the cost slope is (22,000-16,000) / (40-30) = 600. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must be adjusted. | The cost slope in Figure x is calculated by inserting relevant values into the cost slope equation. For example, for activity C the cost slope is (22,000-16,000) / (40-30) = 600. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must be adjusted. | ||
| − | [[File:trade.png| | + | [[File:trade.png|600px|thumb|center|Figure x: setja heimild]] |
=Comparison to related project management technique= | =Comparison to related project management technique= | ||
Revision as of 15:34, 14 September 2016
The Critical Path Method is a step by step technique that is used to schedule a set of project activities. It analysis what activities are least flexible and the project duration is predicted based on the activities that fall along the critical path. The critical path is the longest sequence of activities in a project plan which must be completed on time in order for the project to complete on the predetermined scheduled date [1]. By delaying an activity on the critical path leads to a delay on the completion time of the entire project as these activities have no slack. Activities along the path cannot start until the predecessor activity is completed. When using CPM to plan a project a graphical diagram is often represented showing how each activity is related to the others [2]. This method is one of several tools that is important to keep the project on track and is convenient for all forms of projects, including research projects, product development, construction industry, maintenance and many more.
A joint venture between the Dupont chemical company and computer firm Remington Rand Univac led to a development of the Critical Path Method in the 1956 to tackle the interrelationships of separate activities within a project schedule [3].
In this article the Critical Path Method (CPM) is described, a step by step guidance on how to apply the method is discussed and the tradeoff between cost and time are analyzed. Furthermore, a comparison to other project management techniques is performed and its limitations and advantages are addressed.
Contents |
Overview
Introduction and purpose of CPM
History
General methodology
Application
CPM graph box layout
CPM network creation
Forward pass
Backward pass
Slack calculation
CPM graph and critical path
Time-Cost Trade-Off
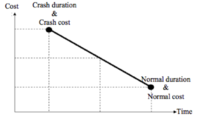
The aim of the time-cost trade-off analysis is to reduce the original project duration, determined from the CPM, to meet a specific deadline, with the least cost. In general, there is a trade-off between the time and the direct cost to complete an activity, the less expensive the resource the larger duration they take to complete an activity. Shortening the duration on an activity will normally increase its direct cost. A simple version of the relationship between the duration of an activity and its direct cost can be seen in Figure x. The normal cost is the least direct cost required to complete an activity, and the corresponding duration is called the normal duration. The crash duration is the shortest duration required to complete the activity and the corresponding cost is called the crash cost.
To solve the time-cost trade-off problem several heuristic approaches can be used, such as the cost slope method. The step by step procedure for that method is summarized as follow:
1. Apply the CPM technique as mentioned in the Application section to identify the critical path.
2. Compute the cost slope for each activity by applying following equation: Cost slope = (crash cost – normal cost) / (normal duration – crash duration)
3. Shorten the activity duration on the critical path that has the least cost slope and has not been shortened to its crash duration.
4. Keep reducing the duration of the activities on the critical path that have the lowest cost slope until its crash duration is reached or until the critical path changes.
5. In some cases, multiple critical paths are involved. The activity(ies) to shorten is determined by comparing the cost slope of the activity on all critical paths with the sum of cost slope for a group of activities.
6. Once a critical path is shortened the duration of the activities and the slack should be adjusted.
7. The cost increase is calculated by multiplying the cost slope with the shortening time of the activities.
8. This heuristic approach should be continued until no further shortening is possible and the crash point is reached.
Example of the time-cost trade-off calculation
The example of this computation was retrieved from….
The aim is to crash the project duration to 110 days. As mentioned in the Application section, the normal project duration is 140 days and the critical path is B-C-D-E. Project total normal cost is the sum the normal cost in Table x, which is 48.300.
The cost slope in Figure x is calculated by inserting relevant values into the cost slope equation. For example, for activity C the cost slope is (22,000-16,000) / (40-30) = 600. Activity D on the critical path has the lowest cost slope and can be crashed by 10 days. The timing for activities that follow activity D must be adjusted.
Advantages of CPM
Disadvantages and limitations of CPM
Conclusion
References
- ↑ Critical Path, BusinessDictionary, 2016.
- ↑ Critical Path Method, webopedia, 2016.
- ↑ History of the Critical Path Method, Kielmas, Maria, 2016.