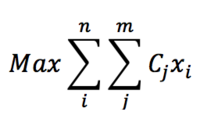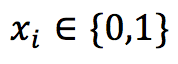Multi-criteria decision making (MCDM) for Project selection
| Line 105: | Line 105: | ||
The spreadsheet used to solve the model can be seen in figure 2. | The spreadsheet used to solve the model can be seen in figure 2. | ||
| − | [[File:Screen Shot 2016-09-15 at 22.02.51.png|center| | + | [[File:Screen Shot 2016-09-15 at 22.02.51.png|center|700px]] |
| + | |||
| + | When the problem is solved a solution is displayed. 11 out of the 20 potential projects should be initiated. Not all resources are utilized fully. There is one Project Manager and 6 Non-technical employees not allocated. The objective function gives 0,678. If all projects were initiated the value would be 1. The total sum of NPV is 764.000$ and the average Risk and Innovation is 5,4 and 6,6 respectively. | ||
| + | The solution should now be evaluated by management before making the final decision. | ||
| + | |||
| + | ==Comparing BIP with sorting method== | ||
| + | A different approach to select the which projects to initiate could be by sorting the score from high to low and then initiate projects until one or more resource groups are used up. The results of this method can be seen in the figure below. | ||
| + | [[File:123.png|center|700px]] | ||
| + | |||
| + | Only 8 projects can be initiated before the expert resource are used up. The value of the objective function is 0,58 witch is lower than 0,68 from the BIP solved model. | ||
| + | |||
| + | More complex sorting systems can be used, but the results can never exceed the optimized method. | ||
| + | |||
| + | ==Project selection including time planning== | ||
| + | |||
| + | ==Supplier portfolio management== | ||
| + | Using MCDM and LP to select suppliers in the supplier portfolio (REF A decision support system for supplier selection using AHP and linear programming | ||
| + | |||
| + | ==Limitations== | ||
| + | |||
| + | ==Annotated bibliography== | ||
Revision as of 21:06, 15 September 2016
Contents |
Abstract
Multi-criteria decision making (MCDM) also called Multi-criteria decision analysis (MCDA) can be used as a decision support tool when making decisions with multiple criteria to evaluate simultaneously. In Portfolio management ensuring that the resources are allocated optimally is a complex task. No company have one single objective to maximize, but several and conflicting objectives to manage simultaneously. MCDM can be used as a decision support tool and provide assistants in the process of making such decisions. MCDM is a good method for selecting which projects a company should initiate. This decision is based on a list of potential projects. All potential projects have assigned values or scores to all criteria’s. The objective function in the model could be to maximize the sum of scores in the selected projects subject to a number of constraints such as available capacity (man hours, budget) and project diversity (at least one project in every category). The decision variables will be which projects to initiate and which not to. This list provides the decision makers with a starting point and augmentation for the decisions made. MCDM relies on assigning all potential projects with values for all criteria. This process can be time consuming so a pre-screening process will in many cases come before the MCDM process.
Big idea
Companies today have a wide range of activities such as manufacturing, innovation, new product development, services and more. It is essential that companies take the right actions. Should the company penetrate a new market, develop new products and services for existing markets, start efficient projects in production and so on. Such activities have potential benefits and request different types and amount of resources. In essence the question is: with projects or activities to initiate to maximize the benefits with respect to the scar resources available? This question seems simple, but in reality it is very complex.
To manage a company efficiently we need to maximize our objectives. Increase profit, reduce costs, increase innovation, reduce lead times, decrease inventory levels and so on. It is then op to management to identify the relevant objectives and witch of them is most important. Furthermore, there are a limited number of resources available. These resources need to be allocated to different activities. Witch projects will achieve the highest possible objective without using more resources then is available? With a small number of objectives and few potential projects this can normally be done by management just discussing the different choices. But if the potential projects are in hundreds and with several objectives many different resource types this can simply not be done without a decision support tool.
Steps in MCDM
Decision processes can follow many different steps with different activities based on what kind of problems the decision makers face. In MCDM the following steps needs to be present.
- Identify criterions
- Weighting of the criterions
- Identify constraints
- Collect data
- Formulate mathematical model
- Solve model
- Evaluate results
- Decision making
Identify criterions
It is important that the objectives are known. This step has a link to the strategy and should be aligned with the overall goals. For example, if a research and development department has a goal of bringing new innovative products to the market place quickly, development time and degree of innovation could be very relevant criterions to include.
Weighting of criterions
When all criterions are identified the weighting of them needs to be undertaken. The weighting is very essential for the results and need to done in a systematic and transparent way. One method is to just assign weights to the criterions. A major benefit from this technique is that it simple and fast. The risks are though that this method will not obtain the “correct” weights. Another possible method is Analytical Hierarchy process (AHP). AHP uses parallel comparison to compute the weights. This gives a more reliable and robust weights. A disadvantage with AHP is that it can be time consuming.
Identify constraints
If there are no constraints the solution will in many cases be to initiate all projects because no scarce resources are limiting the number of projects that can be initiated. Constraints can be divided into two main categories: Resource- and Political constraints.
Resource constraints insure that the number of resources allocated not exceeds the number of resources available.
Political constraints are rules that needs to be complied. A portfolio manager for a dairy products in a supermarket chain could have a political constraint saying that at least 30% of all dairy products need to organic.
Collect data
To facilitate MCDM data is needed. If each potential projects should be evaluated by a number of criterions and constraints this information needs to be present. Values for all criterions and resource consumption are normally the information needed.
Formulate a mathematical model
Based on the weights and criterions will the objective function be formulated. The objective function is what we want to maximize or minimize eg. profit or cost. In a MCDM model we will have more than one criteria in the objective functions and in some mathematical models we will have several objective functions. All identified constraints are formulated. Constraints can both be equalities, inequalities and functions.
Solve model
Based on the type of mathematical model a suitable technique for solving the problem is picked. An example is If objective function and all constraints are linear the problem can be solved by using the simplex method. The result will be the values of the decision variables. These variables could be as simple as 1 and 0 that show if a project should be initiated or not (1=yes, 0=no).
Evaluate results
In this step will the decision makers evaluate the computed results. A model cannot include all aspects of the real world and the results needs be understood hereafter. The result can also be used as argumentation.
Project selection process
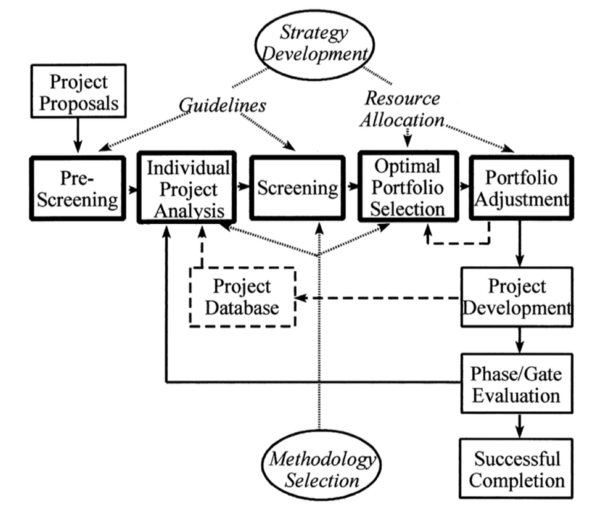
The process of selecting witch projects to initiate evolves several steps. Archer and Ghasemzadeh (1999) present a framework for portfolio selection in new product development (NPD). This framework is specially developed for NPD portfolio, but project portfolio selection could follow similar steps. In figure 1 is an illustration of the framework.
Multi-criteria decision making (MCDM) theory Multi-criteria decision making (MCDM), also called Multi-criteria decision analysis, is developed in the 1950s and 1960s (REF Multiple Criteria Decision Making: From Early History to the 21st Century p).
Types of MCDM
Why the need of portfolio management? Project selection - part of portfolio management
Application
To show how MCDM can be applied in project selection we will go through the steps and formulation a binary linear programming model (FIND REF TIL BLP).
case
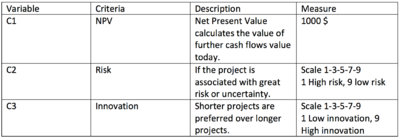
The objective is to make a model to help a Portfolio manager in deciding which development projects to initiate to maximize the objectives. The company have five criterions identified based on the overall strategy in the company. The objectives are listed and explained in the following table.
The criterions are then weighted. NPV is the most important and is weighted 0.5. Innovation is the second most important and is weighted 0.3. Risk the least important of the three criterions and is rated 0.2.
Constraints
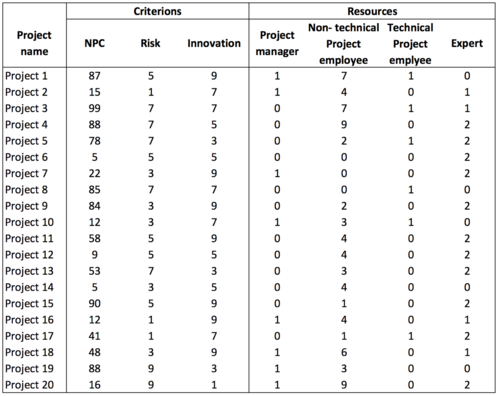
In this example is there two types of constraints. The most important constraint is resource constraint. All personal is divided into four different categories: Project manager, Non-technical Project employee, Technical Project employee and Expert. There are limitations on the number of resources that can be used for each of these four personal groups. Five project managers are available. 50 non-technical Project employees are available. Only five Technical Project employees available and 10 experts. There is also one political constraint that stats that Project 1 must be initiated. Collect data Based on the three criterions and the four resource data on how the different projects are performing in the criterions and the number of resources each project consume of each resource type. These data can be seen in table 1.
There are limitations on the number of resources available. The total amount of available resources can be seen in the table below.
Only 5 Project managers and 5 Technical Project employees are available. 50 Non-technical Project employees are available and 10 experts.
Formulate mathematical model
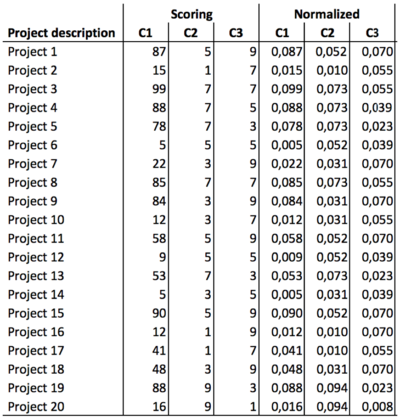
To include criterions with different scales the number needs to be normalized. This is done by dividing each score by the sum of all scores for that criteria. All normalized criterion scores can be seen in the figure below. C1 is NPV, C2 is Risk and C3 is Innovation.
The problem is formulated as a Binary Integer Programming (BIP) problem. This means that the decision variables all are binary (0 or 1), Initiate a project gives the value 1 and if a project should not be initiated the value will be zero.
Objective function:
Resource constraint: Resources must not exceed the available resources:
Political constraint:
Specific projects must be initiated. This is formulated by making a constraint that a specific x must be equal to 1. In this example must Project 1 be initiated. This is formulated as following:
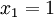each project can only be initiated ones and it is not possible to do a fraction of the project. This is formulated so the decision variables must be binary.
Solve model
There are many different programs that can solve a BIP problem. In this example will OpenSolver be used. OpenSolver is a spreadsheet based solver. This mean that the problem can be formulated in excel and solved by the add-on program OpenSolver.
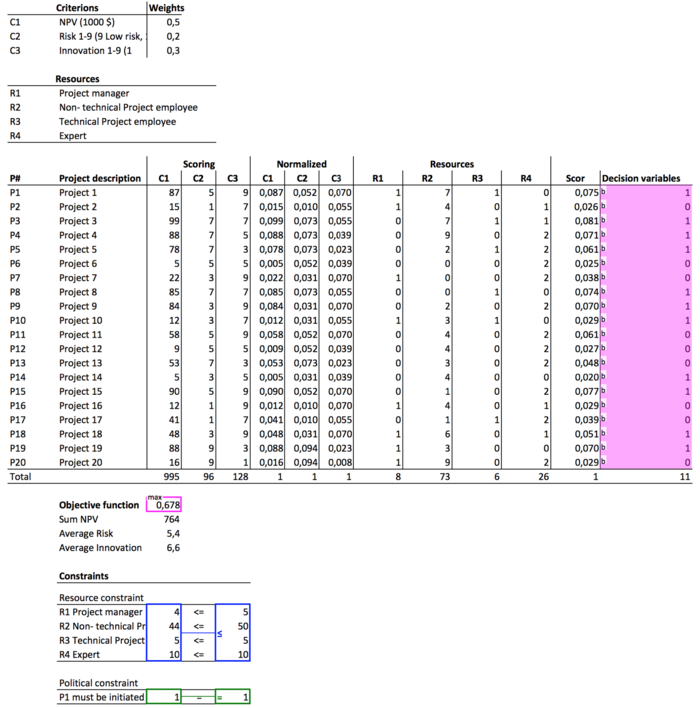
The spreadsheet used to solve the model can be seen in figure 2.
When the problem is solved a solution is displayed. 11 out of the 20 potential projects should be initiated. Not all resources are utilized fully. There is one Project Manager and 6 Non-technical employees not allocated. The objective function gives 0,678. If all projects were initiated the value would be 1. The total sum of NPV is 764.000$ and the average Risk and Innovation is 5,4 and 6,6 respectively. The solution should now be evaluated by management before making the final decision.
Comparing BIP with sorting method
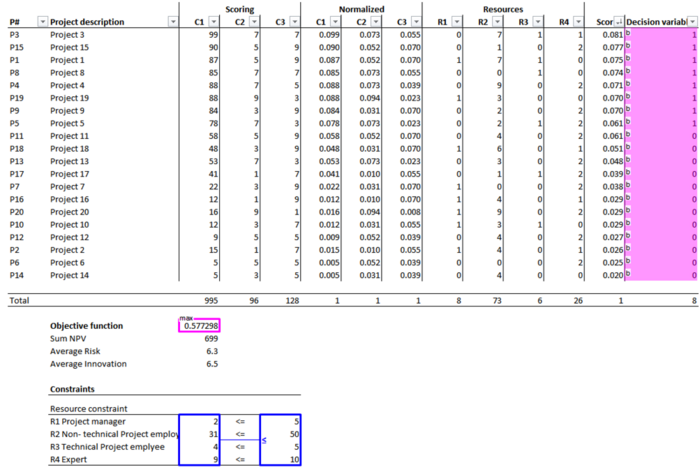
A different approach to select the which projects to initiate could be by sorting the score from high to low and then initiate projects until one or more resource groups are used up. The results of this method can be seen in the figure below.
Only 8 projects can be initiated before the expert resource are used up. The value of the objective function is 0,58 witch is lower than 0,68 from the BIP solved model.
More complex sorting systems can be used, but the results can never exceed the optimized method.
Project selection including time planning
Supplier portfolio management
Using MCDM and LP to select suppliers in the supplier portfolio (REF A decision support system for supplier selection using AHP and linear programming
