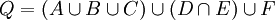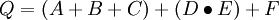Fault Tree Analysis in Projects

Revision as of 17:00, 16 September 2016

Fault tree analysis (FTA) is defined by the International Electrotechnical Commission (IEC) and the International Organization for Standardization (ISO) as a "technique for identifying and analysing factors that can contribute to a specified undesired event".[citation]

FTA has its wide range of application in many fields of engineering such as systems engineering, reliability engineering, and safety engineering. It also serves as an applicable tool for identifying the causes of undesired events in projects.[citation] Undesired events in projects can for instance be exceeding the budget, time delays, lack of team synergy, or any other events that have a negative effect on the project. This is referred to as the top event.

The purpose of FTA is to give both a qualitative and quantitative analysis of the factors that can trigger the undesired top event. A qualitative analysis shows via a graphical representation of a tree the top event that is to be analysed, along with the pathway of all the intermediate and basic events that leads up to the top event. A quantitative analysis shows the probability of a top event being triggered by the input probabilities of the basic events that leads up to the undesired event. The quantitative analysis is calculated through Boolean algebra.[citation]

History

Methodology

Figure 1: An example of a fault tree analysis where exceeding the budget limits is the top event.

FTA is based on the analysis of a top event. This is an event that is believed to be of great importance to the project or an event which has not been given enough attention. A top event needs to be defined as a failure, as it is an undesired event that is to be avoided. Examples of such events can be the delayal of the project if time is considered a constraint. Other projects may be funded by a tight budget where it is crucial to stay within the budget's limits, therefore a top event could be failure to meet the expected budget. Only one top event can be chosen for each fault tree, however it is often recommended to develop several fault trees[citation] each with their different top events if the project is of a large scale or if several top events are of great importance, such as the safety in a powerplant.

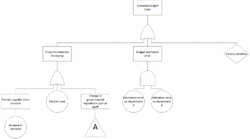
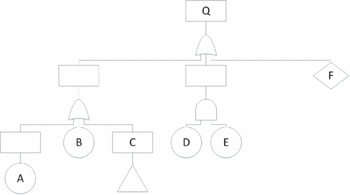
Once a top event has been chosen, the causal factors for said event needs to be identified. Figure 1 is a representation of a basic fault tree with "Exceeded budget limits" as the top event. Beneath it all the causal factors located, that may trigger the top event. The graphical illustration of the fault tree consists of symbols with the intended purpose of clarifying the different relations between the different causal factors.

Symbols

Symbol	Description
Event	An event is one of the causal factors that can occur during the progress of a project. This event will be responsible to fully or partially trigger the event located at an upper level. For the example in Figure 1 it can be seen on the far left that an increase in demand will result in the primary supplier being short on stock, which then results in prices on materials increasing. The increase in prices will then lead to to the top event, which is a failure to complete the project within the budget.
Base event	A base event is an event that is not analysed further because a further analysis on said event has been deemed not useful.[citation] Whether to further investigate an event or not is up to the project members, however it is important to indicate all base events as they are later used in the quantitative analysis of the fault tree. For instance in Figure 1 it was deemed unnecessary to find further causal factors for a market crash, as the project members may have considered the causal factors to be outside the scope of the project or if they deemed it impossible to mitigate or treat the risks associated with any further causal factors.
Unfinished event	Some events may not be of interest to the project at the current time, but may be of importance later in the project. These events are marked with this symbol so that the causal factors may be developed at a later stage in the project. An example is given in Figure 1 on the far right, where the project members were not currently interested in the causal factors for penalties but may develop these later in the project.
Transfer	Many projects will have multiple fault trees developed with each of their own specific top event. Some of these fault trees may have many large portions identical with each other. In an effort to keep the many different fault trees as short and easily read as possible, transfer symbols may be used to indicate that the identical causal factors can be seen in another fault tree. Figure 1 shows a transfer symbol under the event for governmental regulations, to indicate that the causal factors for this event can be found in another fault tree, in order to not repeat the exact same causal factors. The transfer symbol in this example is marked with an "A" to differentiate between many other transfer symbols.
OR gate	OR gates are used to describe the relations between the different causal factors in the same level. The OR gate indicates that any of the events beneath the gate can trigger the event above. As an example to this, Figure 1 indicates that there are 3 causal factors that can trigger the event where prices on materials increase. Either one of the 3 causal factors can trigger the upper event as they are not dependent on each other, therefore it is sufficient that just one of these events occur in order for the prices of material to increase. OR gates are indicated by a sum in the quantitative analysis using Boolean algebra.
AND gate	AND gates are similar to OR gates, however now the causal factors depend on each other. An upper event will not occur until all of the causal factors under the AND gate occur. Figure 1 shows that in order for a budget estimation error to happen, not only must department A make make the error but department B must also make the error for the estimation error to occur after the gate. If only one of the departments make the error but the other don't, then the upper event will not occur as the AND gate has not been satisfied. AND gates are indicated by a product in the quantitative analysis using Boolean algebra.

Boolean algebra

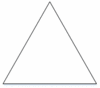
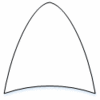
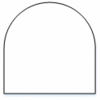
Figure 2: An example of a fault tree analysis.

Boolean algebra can be used for a quantitative analysis of a fault tree. By using Boolean algebra, it is possible to calculate the probability of different events, as well as the top event to occur. Figure 2 is the same fault tree as the previous fault tree in Figure 1, and all of the base events have been assigned a letter to identify them, with the assumption that the events governmental regulations and penalties are also base events. The top event is furthermore assigned the letter Q. For the quantitative analysis only the base events are of interest because they are the lowest causal factors, therefore the intermediate causal factors are of no importance to the analysis and are left blank.

OR gates denote a sum because the base events do not depend on each other while AND gates denote a product because the base events depend on each other. The algebraic representation of the fault tree thus becomes:

Which can be rewritten as:

If the probabilities of the base events are known, it is then possible to calculate the probability for the top event, Q, to occur. Based on the equation from Boolean algebra, it is possible to find the different paths that can occur in the fault tree for the top event to occur. These different paths are referred to as cut sets.^[1] For instance if base event A occurs, then the top event will be triggered. The same goes for base events B, C, and F. However failure on base event D does not trigger the top event due to the AND gate, therefore a possible cut set with base event D would be DE as it requires base event E to occur as well. It is especially interesting in the case of a fault tree analysis to look at minimal cut sets, which are defined as the minimal amount of combinations of the base events that can cause the failure of the top event.

Application

minimal cut sets

Example

Strengths and weaknesses

Limitations

See also

• Event Tree Analysis (ETA)
• Failure modes and effects analysis (FMEA)
• Risk management

Further reading

Annotated bibliography

1. ↑ (1) http://wiki.doing-projects.org/index.php/Use_of_Business_Model_Canvas_to_Kickstart_the_project_management