Test15

Revision as of 10:37, 12 July 2017

Decision making is one of the most important tasks in the management process and it is often a very difficult one. When having knowledge regarding the states of nature, subjective probability estimates for the occurrence of each state can be assigned. In such cases, the problem is classified as decision making under risk ^[1]. In the decision making process, all relevant information is evaluated through decision analysis (DA). The decision analysis process consists of the use of a decision tool and a decision theory. The decision tree is the most commonly applied decision tool in the decision analysis ^[2]. The decision theory of interest in the decision analysis, regarding the decision making under risk, is the expected value of criterion also referred to as the Bayesian principle. This is the only one of the four decision methods that incorporates the probabilities of the states of nature ^[3].

Methologdy

Risk analysis and risk management is an important tool in the construction management process. Risk implies a degree of uncertainty and an inability to fully control the outcomes or consequences of such an action. The objective of a decision analysis is to discover the most advantageous alternative under the circumstances ^[4].

Decision analysis is a management technique for analyzing management decisions under conditions of uncertainty ^[5]. The decision problems can be represented using different statistical tools applied to the mathematical models of real-world problems. An important and relevant decision tool to represent a decision problem is a decision trees. A decision tree is a graphical representation of the alternatives and possible solutions, also challenges and uncertainties. In decision analysis, formulating the decision problem in terms of a decision tree is a favorable visual and analytical support tool, where the expected values of competing alternatives are calculated.

Theory and principles

The following provides the theory and principles behind the decision making under risk, using Bayesian decision analysis. An overview of the principles and construction regarding the decision tree is provided as well as the decision theory regarding the decision tree analysis.

Decision tree

A decision tree (DT) is a chronological representation of the decision process. It is particularly suitable where a series of decisions are to be established and/or several outcomes appear at each stage of the decision -making process, it is therefore convenient in analyzing multi-stage decision processes. The number of alternative actions can be exceptionally large and an outline for the systematic analysis of the corresponding consequences is therefore expedient.

Decision trees is an effective decision tool in the decision-making, because it:

Figure 1: Decision tree diagram^[6] (click to zoom)

Provides a clear overview of the situation so that all possibilities can be investigated

Allows to fully analysis the potential consequences of a decision

Provides an outline in which to compute the values of consequences and the probabilities of achieving them.

Assists obtaining the best decisions based on existing information and best estimates.

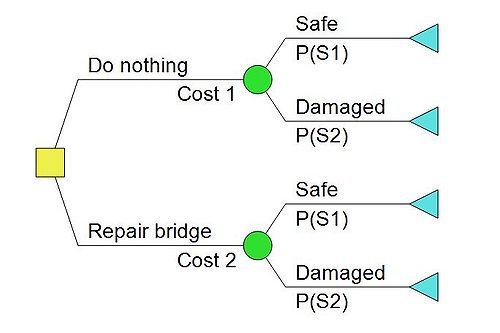
A decision tree is a schematic, tree-shaped diagram representation of a problem and all possible courses of action in a particular situation and all possible outcomes for each possible course of action. The diagram is constructed of branches and each branch of the decision tree represents a possible decision, occurrence or reaction see figure 1. The tree is structured to show how and why one choice may lead to the next, with the use of the branches indicating each option is mutually exclusive.

A decision tree consists of three types of nodes:

Decision (choice) Node

Chance (event) Node

Terminal (consequence) Node

There is no universal set of symbols applied when constructing a decision tree but the most common ones is a square to represent the decision node, a circle for the chance event and a triangle for the terminal node.

Construction of decision tree

For the purpose of illustrating the construction of a decision tree, the following considers a simple decision problem. An old bridge has been subject to deterioration, control data reveal that the bridge structure may be damaged. However, this cannot be indicated with certainty. If the bridge is damaged, it is unfit for service and a new one needs to be constructed. Your company is hired to find the best solution of two alternatives:

Alternative a₁: Do nothing
Alternative a₂: Repair the bridge

The decision-making process involves evaluating weather is more beneficial to do nothing or repair the bridge, the alternative associated with the lowest risk is in this case the alternative with the lowest expected cost.

Figure 2: Decision tree (click to zoom)

Figure 2 illustrates the constructed decision tree related to the provided example. The diagrams are created by the author using the program ‘'DPL9'’ which is decision tree-based, decision analytic software tool, developed by Syncopation Software ^[7]. The tree is constructed from right to left in following three steps:

The first node drawn is the decision node, a branch emanating from a decision node corresponds to a decision alternative, which in this case are either to repair the bridge or do nothing. It includes a cost or benefit value, which in this example is referred to as cost 1 and cost 2. The decision node is displayed as a yellow square.

The next node is the chance node, since either of the alternatives does not lead to a new the decision. A branch emanating from a state of nature node (chance node) corresponds to a particular state of nature, and includes the probability of this state of nature. For both alternatives the branches has the same outcome, either the bridge is safe and fit for service or the bridge is damaged and a new needs to be constructed. The probability associated with the bridge being safe or damaged, are denoted P(S1) and P(S2), respectively. The chance node is illustrated whit a green circle.

The final node is the terminal node, this represent the cost consequence related to the choice of decision branch for all possible outcomes. The value of the each terminal node, are the total sum of the cost related to each branches. This value is also called the net path value (NPV). The terminal node is presented by the use of a blue triangle.

Decision theory

Decision theory is an analytical and systematic approach to tackle problems. Decision theory is the part of probability theory that is quantifying the consequences of uncertain decisions. This can be applied to state the objectivity of a choice and to optimize decisions ^[8].

The decision method applied in decision making under risk, is the expected value of criterion, because it incorporates the probabilities of the states of nature. The expected value of criterion contains the analysis of the expected monetary value (EMV), or simply expected value, which is the foundational concept on which decision tree analysis is based. EMV is a tool and technique, a numerically analyze performed concerning the influence of identified risks on overall project objectives. The EMV of risk is:

Expected Monetary Value= Probability of the Risk x Impact of the Risk.

EMV computes the average outcome when the future contains uncertain situations; it is the sum of the different scenarios connected to the chance node. The decision made at the decision nodes is therefore based on the expected monetary values of the related alternatives. Depending on the state of information regarding the probability at the time of the decision analysis, three different analysis types are distinguished, namely prior analysis, posterior analysis and pre-posterior analysis. Each one of these is important in practical applications of decision analysis and the basic theory is therefore outlined briefly in the following, with the utility represented in the simplified manner through costs.

Prior analysis

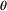The prior analysis, is a decision analysis performed with known information, it quantify the beliefs before any evidince is taking into account. At this stage, the probabilistic description $\scriptstyle P[\theta]$ of the state of nature $\scriptstyle \theta$ is usually called a prior description and called $\scriptstyle P'[\theta]$ . When the probabilities of the various state of nature corresponding to different consequences have been estimated, and the consequences for the final outcome determined, the analysis consists of the calculation of the expected utilities corresponding to the different action alternatives.

The optimal decision is identified as the expected cost, $\scriptstyle E'[C]$ , when the decision is based on the prior information. The expexcted cost is equal to the expected value of the action alternative coorsponding to the largest expected utility. When determing the expected cost, the decision maker is also doing the decision of which action to take.

Posterior analysis

The posterior analysis is the conditional probablilty that is assigned when additional information becomes availble. The conditional probabilities form the basis of updating of probability estimates based on new information, knowledge or evidence, which makes conditional probabilities of interest in risk and reliability analysis.

The conditional probability is the probability of an event, given that another event has already accord. The posterior probability of an event 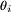$\scriptstyle \theta_i$ , given that another event 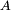$\scriptstyle A$ has occured is therefore expresed as:

${P''[\theta_i | A] = \frac {P[A|\theta_i] P' [\theta_i]} {P[A]}}$

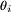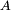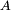The conditional term $\scriptstyle{P[A|\theta_i]},$ can be referred to as the likelihood, the probability of observing a certain state given the true state. The term $\scriptstyle{P'[\theta_i]},$ is the prior probability of the event $\scriptstyle \theta_i$ , prior to the knowledge about the event $\scriptstyle A$ . $\scriptstyle{P[A]},$ is the probability of the event $\scriptstyle A$ , i.e. $\scriptstyle{P[A]},$ , can be written as:

${P[A]=\sum_{i=1}^n P[A|\theta_i] P' [\theta_i]}$

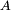Having determined the updated probabilities, the probabilites is assigned the different actions. The calcultions of the expected values is excuvated and the expected cost related to the postereier anaylsis is denoted $\scriptstyle E''[C|A]$ . The notation show that the value of the expected cost is pased upon conditional probabaility, so the expected cost depending on the fact that the event $\scriptstyle A$ has occured.

Pre-posterior Analysis

The objective of preposterioe analysis is to determine the whether the value of the prediction is greater or less than the cost of the information. Posterior refers to the revision of the probabilities and the pre indicates that this calculation is preformed before paying the fee. The goal is therefore to choose the experiment or experimental design whit largest utility ^[9]. The pre-posterior analysis is like the porsterioe anlysis, a analysis that consist of the determination of the conditional probabilities. While the posterior analysis is based on the fact that event A has occured the pre-porsttior analysis, takes in the probability of the event A even occuring. The excpected cost based on the preposterier analysis is therefore expressed as:

${E[C]=\sum_{i=1}^n P'[A_i] E'' [C |A_i]}$

where $\scriptstyle n$ is the number of different possible experiment findings. The posterior expected cost $\scriptstyle {E'' [C |A_i]}$ for the different experiment findings, is therefore a process of prefroming the pre-posterior analysis. The probability $\scriptstyle {P' [A_i]}$ is the prior probabilities of the different events.

Baysian decision analysis

The theory and principles of decision making under risk has been presented. The theory is applied to different examples. The data used in the examples is fictive and cosntructed by the author and is therefor comparible to any true data. The scenarios in the examples is, however, representing situations that are presentive for the decision making under risk when managing constructions.

Example 1 - Prior analysis

The prioir analysis is related to the condition of known information. The same scenario represented previous under the construcion of the decision tree, is used. The two alternatives is either to do nothing or to repair the bridge. The following information is now provided:

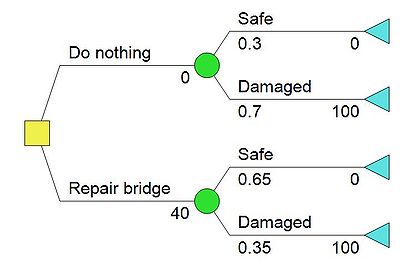
It is estimated that there is a 10% probability that the bridge structure is safe. If the bridge is repaired then the probabaility of the bridge stucture having damaged is 20%. Table 1 provides the probabilities used in the construcion of the decision tree in figure 3.

	a₁- Do nothing	a₂- Repair bridge
$\scriptstyle P[\theta_1]$ - Safe	0.1	0.8
$\scriptstyle P[\theta_2]$ - Damaged	0.9	0.2

Table 1: Probabilities related to the two alternatives

Figure 3: Decision tree example 1 - prior analysis (click to zoom)

If the bridge structure is damaged, then a new bridge is reqiured which is asssociated with a cost of $100 mio. If the structure is safe then the cost is $0. If it chosen to repair the bridge, cost of the the reperation $20 mio. Looking at figure 2, the value related to cost1 is $0mio. and cost2 is $20mio. The construction of the decesion tree is the first step in the decision making. The two alternatives are provided with the related costs, the branches alternating from the decision nodes is provided with the probabilities of state of nature, that are presented in table 2 and the related costs. In this case, the cost when the bridge is safe is $0 mio. and the cost if the bridge is damaged is $100 mio., due to the fact that if the bridge is damages, then the construction of a new bridge is required. Having the informations regarding the costs and the probabilities to the decision, the decision tree related to this case can be seen in figure 3. The net pressure value is not represented at the end nodes, which is due to the fact the decision tree is drawn in DPL9 and the program is calculating the value at the end nodes, when the decision analysis is preformed. Therefore the branches are provided with their individual, related values. For simplicity the net pressure values are shown in table 3.

	a₁- Do nothing	a₂- Repair bridge
NPV ₁ - Safe	$0mio.	$20mio.
NPV ₂ - Damaged	$100mio.	$120mio.

Table 2: Net pressure values related to the two alternatives - example 1

The decision analysis is preformed, by first caculating the expected value , the calculations are done from left to right, starting with the chance nodes having branches ending in the final nodes.

1. chance node - associated with alternative a ₁

$\scriptstyle EVM_1=P[\theta_1] \cdot NPV_1 + P[\theta_2] \cdot NPV_2=0.1 \cdot $0mio. + 0.9 \cdot $100mio.= $90mio.$

2. chance node - associated with alternative a ₂

$\scriptstyle EVM_2=P[\theta_1] \cdot NPV_3 + P[\theta_2] \cdot NPV_4= 0.8 \cdot $20mio. + 0.2 \cdot $120mio. = $40mio.$

The excpected monetary value at the chance nodes has now been calculated. The expected cost at the decsion nodes is based on the expected monetary value for the two alternatives. In this example the utility is represented in a simplified manner through the costs whereby the optimal decisions is identified as the decisions minimizing expected costs, which then is equivalent to maximizing expected utility. The expected cost based on the prior information is therefore:

$\scriptstyle E'[C]=min \{EVM_{a_1};EVM_{a_2} \}=$40mio.$

Alternative a ₂, repair the bridge....

Figure 4: Decision analysis example 1 - prior analysis (click to zoom)

Figure 4 show results of the decision analysis preformed in DPL9. In figure 4 the net path values are given at the terminal nodes, as well as the expected values at the chance nodes. The branch representing alternative a ₂, is bold, confirming decision way.

Example 2 - Prosterior analysis

When additional information becomes available, the probability structure in the decision problem may be updated. The same situation and condition as in example 1 is being investigated, having that all the prioir information related to cost and porbaility are the same. In this example more information about the bridge repairment is obtained:

Through a study that costs $5mio. the study gives

Having updated the probability structure the decision analysis is unchanged in comparison to the situation with given prior information. The same condition and information provided in example 1 is used. Now acquired more information through a study about the chances of a bridge repairment. The study costs $5mio. Table 3 contains the estimation of the success rate (structure safe) of the bridge repairations in the study.

	Structure safe	Structure damaged
Indication I	0.9	0.1

Table 3: Bridge repair results

Figure 5: Decision tree example 2 - posterior analysis (click to zoom)

Given the result of the study, the updated conditional probability or the posterior probability $\scriptstyle P''[\theta_i | I ]$ is evaluated by use of the Bayes' rule. The likelihood of the structure being safe $\scriptstyle P[I|\theta_1]=0.9$ and likelihood of the strucutre being damaged is $\scriptstyle P[I|\theta_2]=0.1$ . The probability of the indication $\scriptstyle P[I]$ is then:

$\scriptstyle {P[I] = P[I|\theta_1] \cdot P' [\theta_1]+ P[I|\theta_2] \cdot P' [\theta_2]=0.3 \cdot 0.9 + 0.7 \cdot 0.1 =00}$

The postorior probabilities are then:

$\scriptstyle {P''[\theta_1 | I] = \frac {P[I|\theta_1] P' [\theta_1]} {P[I]}}= \frac {0.9 \cdot 0.7} {00}$

$\scriptstyle {P''[\theta_2 | I] = \frac {P[I|\theta_2] P' [\theta_2]} {P[I]}}= \frac {0.1 \cdot 0.3} {00}$

The cost the studies needs to be accounted for, which changes the prior costs for the situation. The cost related to doing nothing is therfore $10 mio. instead of the previous $0 mio. and the cost the repairemnt of the bridge is $30 mio. Having the informations regarding the costs and the probabilities to the decision, the decision tree related to this case can be seen in figure 5. The net pressure values is shown in table 4.

	Structure safe	Structure damaged
NPV₁	0.9	0.1
NPV₂

Table 4: Net pressure values example 2 - posterior analysis

Having determined the updated probabilities, the expected monetary values is then:

1. chance node - associated with alternative a ₁

$\scriptstyle EVM_1=P[\theta_1] \cdot NPV_1 + P[\theta_2] \cdot NPV_2=0.1 \cdot $0mio. + 0.9 \cdot $100mio.= $90mio.$

2. chance node - associated with alternative a ₂

$\scriptstyle EVM_2=P''[\theta_1 | I] \cdot NPV_1 + P''[\theta_2 | I] \cdot NPV_2= 0.8 \cdot $20mio. + 0.2 \cdot $120mio. = $40mio.$

The posterior expected cost $\scriptstyle E''[C|I]$ of the utility corresponding to the optimal action alternative is readily obtained as:

$\scriptstyle E''[C|I]=min \{EVM_{a_1};EVM_{a_2} \}=$40mio.$

Considering the additional information, it is seen that the optimal decision has been switched to action a2 as compared to the prior decision analysis. Alternative a ₂, repair the bridge....

Figure 6: Decision analysis example 2 - posterior analysis (click to zoom)

Figure 4 show results of the decision analysis preformed in DPL9. In figure 4 the net path values are given at the terminal nodes, as well as the expected values at the chance nodes. The branch representing alternative a ₂, is bold, confirming decision way.

Example 3 - Pre-Postrior analysis

Often the decision maker has the possibility to ‘buy’ additional information through an experiment before actually making his/her choice of action. If the cost of this information is small in comparison to the potential value of the information, the decision maker should perform the experiment. If several different types of experiments are possible, the decision maker must choose the experiment yielding the overall largest expected value of utility. The conditional probability is used in the pre-posterioe analysis, for the simplicity a new example is taken is taken

↑ Khalili Damghani, K., M. T. Taghavifard, and R. Tavakkoli Moghaddam (2014). “Decision Making Under Uncertain and Risky Situations.” (22-06-2017)
↑ R.C. Barros, A. de Carvalho, A.A. Freitas, Automatic Design of Decision-Tree Induction Algorithms, SpringerBriefs in Computer Science, Springer International Publishing, New York City. URL https://books.google.co.kr/books? id¼PFqEBgAAQBAJ, 2015. (22-06-2017)
↑ Figueira, José, Salvatore Greco, and Matthias Ehrgott. Multiple Criteria Decision Analysis : Springer, 2006. (22-06-2017)
↑ Knight, F. H. (1921) Risk, Uncertainty, and Profit
↑ COVELLO, VT. “DECISION-ANALYSIS AND RISK MANAGEMENT DECISION-MAKING - ISSUES AND METHODS.” Risk Analysis 7.2 (1987): 131–139.
↑ https://www.lucidchart.com/pages/decision-tree
↑ https://www.syncopation.com/products-main
↑ Wu, G., Zhang, J. and Gonzalez, R. (2004) Decision Under Risk, in Blackwell Handbook of Judgment and Decision Making
↑ Berger, James O. “Statistical Decision Theory and Bayesian Analysis.” Preposterior and Sequential Analysis 7 (1985): 432-520.

Karabadji, Nour El Islem et al. “An Evolutionary Scheme for Decision Tree Construction.” Knowledge-based Systems 119 (2017): 166–177. Web. (basis for decision tree)

R.C. Barros, A. de Carvalho, A.A. Freitas, Automatic Design of Decision-Tree

Induction Algorithms, SpringerBriefs in Computer Science, Springer International Publishing, New York City. URL https://books.google.co.kr/books? id¼PFqEBgAAQBAJ, 2015.

Delmar, M.V., and J.D. Sorensen. “Probabilistic Analysis in Management Decision Making.” Proceedings of the International Offshore Mechanics and Arctic Engineering Symposium 2 (1992): 273–282. Print.

Donegan, H. A. “Decision Analysis.” Sfpe Handbook of Fire Protection Engineering, Fifth Edition (2016): 3048–3072. Web.

Khalili Damghani, K., M. T. Taghavifard, and R. Tavakkoli Moghaddam. “Decision Making Under Uncertain and Risky Situations.” (2014): n. pag. Web.

Annotated:

Goodwin, Paul; Wright, George. (2004). Decision Analysis for Management Judgment. Wiley

[Khalil-0] Khalili Damghani, K., M. T. Taghavifard, and R. Tavakkoli Moghaddam (2014). “Decision Making Under Uncertain and Risky Situations.” (22-06-2017)

[Barros-1] R.C. Barros, A. de Carvalho, A.A. Freitas, Automatic Design of Decision-Tree Induction Algorithms, SpringerBriefs in Computer Science, Springer International Publishing, New York City. URL https://books.google.co.kr/books? id¼PFqEBgAAQBAJ, 2015. (22-06-2017)

[Figueria-2] Figueira, José, Salvatore Greco, and Matthias Ehrgott. Multiple Criteria Decision Analysis : Springer, 2006. (22-06-2017)

[Knight-3] Knight, F. H. (1921) Risk, Uncertainty, and Profit

[Covello-4] COVELLO, VT. “DECISION-ANALYSIS AND RISK MANAGEMENT DECISION-MAKING - ISSUES AND METHODS.” Risk Analysis 7.2 (1987): 131–139.

[5] ttps://www.lucidchart.com/pages/decision-tree

[6] ttps://www.syncopation.com/products-main

[Wu-7] Wu, G., Zhang, J. and Gonzalez, R. (2004) Decision Under Risk, in Blackwell Handbook of Judgment and Decision Making

[Berger-8] Berger, James O. “Statistical Decision Theory and Bayesian Analysis.” Preposterior and Sequential Analysis 7 (1985): 432-520.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

@@ Line 58: / Line 58: @@
   <ol>
    <li>The first node drawn is the decision node, a branch emanating from a decision node corresponds to a decision alternative, which in this case are either to repair the bridge or do nothing. It includes a cost or benefit value, which in this example is referred to as ''cost 1'' and ''cost 2''. The decision node is displayed as a yellow square. </li>
    <li>The next node is the chance node, since either of the alternatives does not lead to a new the decision. A branch emanating from a state of nature node (chance node) corresponds to a particular state of nature, and includes the probability of this state of nature. For both alternatives the branches has the same outcome, either the bridge is safe and fit for service or the bridge is damaged and a new needs to be constructed. The probability associated with the bridge being safe or damaged, are denoted P(S1) and P(S2), respectively. The chance node is illustrated whit a green circle. </li>
    <li> The final node is the terminal node, this represent the cost consequence related to the choice of decision branch for all possible outcomes. The value of the each terminal node, are the total sum of the cost related to each branches. This value is also called the net path value (NPV). The terminal node is presented by the use of a blue triangle. </li>

Test15

Revision as of 10:37, 12 July 2017

Contents

Methologdy

Theory and principles

Decision tree

Construction of decision tree

Decision theory

Prior analysis

Posterior analysis

Pre-posterior Analysis

Baysian decision analysis

Example 1 - Prior analysis

Example 2 - Prosterior analysis

Example 3 - Pre-Postrior analysis

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox