Femern
| Line 20: | Line 20: | ||
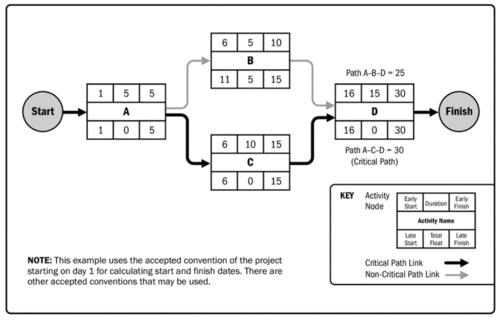
The critical path method is used to produce to calculate the minimum project duration and the amount of schedule flexibility available on the logical network paths within the schedule model. The analysis calculates the early and late start and finish dates of each activity using activity duration estimates. Using the scheduled activity network, the longest activity path (namely 'critical path') is then computed. This is used as the project duration estimate. The 'float' of activities not on the critical path is determined, defined as the maximum duration the activity can be delayed by without delaying the project as a whole. This is used to determine the schedule flexibility within the schedule model. | The critical path method is used to produce to calculate the minimum project duration and the amount of schedule flexibility available on the logical network paths within the schedule model. The analysis calculates the early and late start and finish dates of each activity using activity duration estimates. Using the scheduled activity network, the longest activity path (namely 'critical path') is then computed. This is used as the project duration estimate. The 'float' of activities not on the critical path is determined, defined as the maximum duration the activity can be delayed by without delaying the project as a whole. This is used to determine the schedule flexibility within the schedule model. | ||
| − | [[File: Example of a Critical Path Method.png |500px|thumb|Figure 1: Example of critical path method]] | + | [[File:Example of a Critical Path Method.png |500px|thumb|Figure 1: Example of critical path method]] |
==Bibliography== | ==Bibliography== | ||
<references/> | <references/> | ||
Revision as of 08:15, 3 March 2020
Contents |
Collection of tools
Plan Quality Management
Manage Quality
Control Quality
Schedule Management
Estimation of Activity Durations: Three-Point Estimating[1]
Three-point estimating is a tool used to estimate the duration of an activity. It is used primarily when there is insufficient historical data available to produce an estimate. The tool considers a most likely time (tM), optimistic time (tO) and pessimistic time (tP) to produce the best estimate via the following equation:
tE = (tM + tO + tP)/3
Using this triangular distribution estimation uncertainty and risk can be reduced with respect to single-point estimating. Total project duration may then be estimated by finding the summation of individual activity durations through an integrated activity execution flow chart (e.g. Gantt chart).
Development of a Schedule: Critical Path Method[1]
The critical path method is used to produce to calculate the minimum project duration and the amount of schedule flexibility available on the logical network paths within the schedule model. The analysis calculates the early and late start and finish dates of each activity using activity duration estimates. Using the scheduled activity network, the longest activity path (namely 'critical path') is then computed. This is used as the project duration estimate. The 'float' of activities not on the critical path is determined, defined as the maximum duration the activity can be delayed by without delaying the project as a whole. This is used to determine the schedule flexibility within the schedule model.
Bibliography
- ↑ 1.0 1.1 https://app-knovel-com.proxy.findit.dtu.dk/web/view/khtml/show.v/rcid:kpGPMBKP02/cid:kt011DX7BB/viewerType:khtml//root_slug:6-project-schedule-management/url_slug:project-schedule-management?kpromoter=federation&b-toc-cid=kpGPMBKP02&b-toc-root-slug=&b-toc-url-slug=project-schedule-management&b-toc-title=Guide%20to%20the%20Project%20Management%20Body%20of%20Knowledge%20(PMBOK%C2%AE%20Guide)%20(6th%20Edition)&page=1&view=collapsed&zoom=1