Net Present Value (NPV)
Written by Deepthi Tharaka Parana Liyanage Don- s203116
Contents |
Abstract
Financial appraisal is a method used to evaluate whether a proposed project or portfolio of investment projects is worthwhile by considering the benefits and costs that result from its execution [1]. Investment decisions of the management are critical to a company since it decides the future of the company. This article discusses the net present value (NPV) method which is widely used in the financial appraisal. NPV is a dynamic financial appraisal method that considers the time value of money by applying discounting to all future payment series during the investment period [1]. In simple terms, the net present value is the difference between the project's future incoming and outgoing cash flows at present time. The calculation of the NPV starts by determining the net cash flows from the difference of future incoming cash flows and outgoing cash flows for each period of an investment. After the net cash flow for each period is calculated, the present value (PV) of each one is achieved by discounting using a suitable discount rate. Net present value is the cumulative value of all the discounted future net cash flows [1] [2].
Firstly, this article discusses the idea behind the net present value method. Then this introduces the NPV calculation method [1] and describes the importance of choosing the suitable discount rate [3]. Also, it discusses the other NPV formula for special cases such as annuity and perpetuity. Then it highlights the decision criteria behind NPV and explains it with real-life applications. Finally, it critically reflects on the limitations [4] of this method and briefly highlights the key references used in this article.
Big Idea
Project business case development is a critical point in the initial stage of the project where it uses to obtain the approval for investing the project by presenting the benefits, cost, and risk associated with alternative options. The business case is produced by the client or the sponsor of the project and the directorate of an organization uses this document to accept or reject the case for carrying out the project [5]. In a business case, financial appraisal plays a key role to answer the fundamental economic questions of whether an investment should be made and which project should be chosen among a selection of different alternatives. Because the task of financial appraisal is to predict the financial effects of planned investment and to present the data in order to get critical investment decisions [1]. The net present value method is one of the most frequently used approaches in the financial appraisal of a project [1] [6].
What is NPV?
Net Present Value (NPV) is the present value of the future net cash flows of an investment. [1]. In other words, NPV is the difference between the present value of all future incoming cash flows and the present value of all future outgoing cash flows. The NPV of a project is calculated based on different assumptions [3] [4] [7] such as:
- Money in the future will not be worth the same amount of money today. Therefore, all the future cash flows are translated to present value by discounting them using a suitable discount rate.
- The discount rate remains the same throughout the life of the project.
- The incoming or outgoing cash flows other than the initial investment occur at the end of each period.
- The cash generated by a project is immediately reinvested at the discount rate.
NPV is a widely used method in the financial appraisal that has the following benefits [4] :
- NPV considers the concept of the time value of money by obtaining the present value of future net cash flows.
- NPV calculation considers the complete life cycle of an investment using the expected future cash flows in different periods of time.
- It has the additive property. That means the possibility to sum the NPV of individual projects to evaluate the project portfolio.
- Reflects the return on capital investments in the best and clearest way.
- NPV method enables the decision-making process for companies by identifying whether a particular investment is profit-making or loss-making.
Time value of money
The net present value considers the time value of money in the analysis, which makes the net present value more precise than other financial appraisal methods. Time value of money means that a sum of money is worth more now than the same sum of money in the future [4] [8]. That is because the money you have now can use to make more money by buying something now and selling it later for more, running a business or depositing it in the bank, and earning interest. Since money can grow only through investing, investment delay is an opportunity cost. That means not having the money right now also includes the loss of additional income, which could be earned by having money earlier. Future money is also less valuable because inflation erodes its buying power. Moreover, receiving money in the future rather than now may involve some risk and uncertainty regarding its recovery. For these reasons, future cash flows are worth less than the present cash flows. NPV assesses the profitability of a given project on the basis that cash flow in the future is not worth the same as a cash flow today. The time value of money is recognized in NPV by applying discounting to all future cash flows generated during the investment period[6].
Discount Rate
The discount rate is the rate used to determine the present value of future cash flows in net present value calculation. The discount rate is a crucial component in determining NPV and the selection of discount rate will be company-specific as it is related to how the company gets its funds [3]. Investments are financed using equity and/or debt and different costs of capital exist. If an investment is financed completely with equity, the discount rate can be derived from a cost of equity or the average return of a similar investment object. Investments that are completely debt-financed can be analysed using the cost of debt. If an investment depends on both equity and debt financing, the discount rate is the weighted average cost of capital (WACC) and can be calculated as the weighted average of the cost of equity and cost of debt [3]. The weighted average cost of capital is often used in companies as the discount rate and it can be interpreted as the minimum rate of return that the investor demands for his investments [1]. For small projects, where it is difficult to identify the equity and debt used for financing a single project, the discount rate is usually assumed to equal the weighted average cost of capital of the whole company [3].
However, it is appropriate to use higher discount rates to reflect other factors such as risk, the opportunity cost of money invested in the infrastructure and etc [2]. An NPV calculated using variable discount rates may better reflect the situation than one calculated from a constant discount rate for the entire investment duration [1].
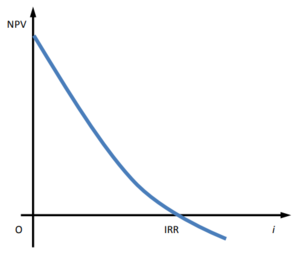
Also, it is important to highlight that the NPV highly depends on the choice about the discount rate, and on the time span considered by the analysis. The choice of the discount rate can dramatically change the net present value since the NPV is an inverse function of the discount rate (i). Higher the discount rate, the smaller the net present value. Also, the discount rate where the net present value is zero is called the internal rate of return (IRR). The time period of analysis influences the NPV because projects, in general, impose a negative cash flow in the first years and positive cash flows only sometime after its entering into operation, a longer period of analysis includes a bigger number of years with a positive cash flows than a shorter period of analysis [2].
Formula
The following formula use these common variables [1]:
| Variable | Meaning |
|---|---|
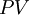
|
Present Value |
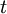
|
Time of the cashflow |
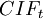
|
Cash inflows in period t |
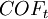
|
Cash outflows in period t |
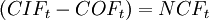
|
Net cash flow in period t |
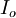
|
Investment in t=0 |
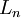
|
Liquidation proceeds in t=n |

|
The discount rate |
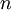
|
Total number of periods |
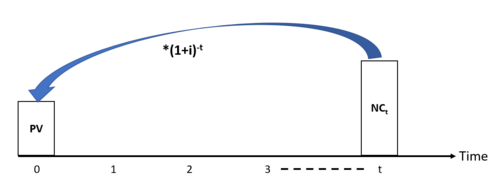
In order to consider the time value of money, the net present value method considers the value of an investment at the present time by projecting all future cash flows into a key figure at the time today. This projection of the value that a future cash flow has in the present is called present value (PV). To get the present value (PV) of a future net cash flow in period t, they are discounted using a discount rate (i) as follows:
Example:
If a project is expected to receive $5,000 with 10% discount rate after 4 years, its present value (PV) can be calculated as:
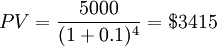
Net present value combines these projections of net cash flows to assess the overall value of a project from the present view. In simple terms, The net present value is calculated from the difference of the present value of all future incoming cash flows(revenues/benefits) and the present value of all future outgoing cash flows(costs) [1]. Therefore the net present value is given by:
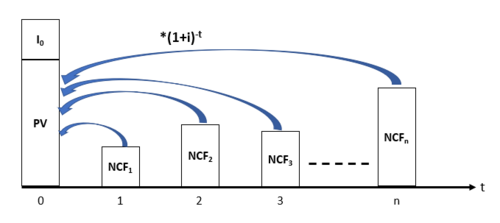
The difference between the cash inflows and cash outflows, 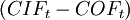 gives the net cash flow,
gives the net cash flow, 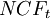 of the corresponding period. For normal investments which are characterized by initial investment,
of the corresponding period. For normal investments which are characterized by initial investment, 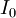 , subtracting the initial investment outlay,
, subtracting the initial investment outlay, 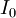 from the present value of the net cash flows gives the net present value. If a possible final payment,
from the present value of the net cash flows gives the net present value. If a possible final payment, 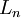 for the liquidation of the investment in t = n is also considered, the calculation of the net present value can be written as follows [1]:
for the liquidation of the investment in t = n is also considered, the calculation of the net present value can be written as follows [1]:
As a summary, the following steps are recommended for the calculation of the net present value [1]:
- Determination of the initial investment,
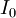 .
.
- Estimate the expected net cash flows,
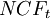 from the investment for each period of the planning period.
from the investment for each period of the planning period.
- Selection of the uniform discount rate,
 .
.
- Determination of the present value through discounting of the expected net cash flows,
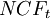 with the discount rate.
with the discount rate.
- Subtraction of the initial investment
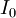 from the present value. This gives the net present value (NPV).
from the present value. This gives the net present value (NPV).
Example:
A company decides to invest $100,000 for a project which is expected to give the following cash flows. Assume the discount rate is 10%. Calculate the NPV of the project.
| Now | Year 1 | Year 2 | Year 3 | |
|---|---|---|---|---|
| Initial Investment | $100,000 | |||
| Running costs | $60,000 | $90,000 | $90,000 | |
| Revenues | $80,000 | $100,000 | $120,000 | |
| Liquidation proceeds | $140,000 |
Using NPV formula NPV can be calculated as follows:
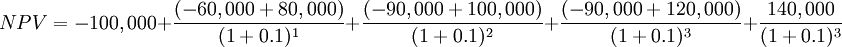
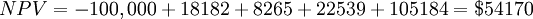
Other NPV Formula
NPV of an annuity
If the net cash inflows are uniform and equidistant and occur at the end of each period, the series of net cash flows can be interpreted as an annuity [1]. The payments or receipts occur at the end of each period for an ordinary annuity while they occur at the beginning of each period for an annuity due. Using the formula for the present value of an ordinary annuity, NPV can be calculated as follows [1]:
Example:
If a company decides to invest $100,000 for a project which is expected to give the following cash flows. Assume the discount rate is 10%. Calculate the NPV of the project.
| Now | Year 1 | Year 2 | Year 3 | |
|---|---|---|---|---|
| Initial Investment | $100,000 | |||
| Net cash flows | $60,000 | $60,000 | $60,000 | |
| Liquidation proceeds | $140,000 |
Using NPV of an annuity formula,
![N P V=-100,000 + 60,000 \cdot\left[\frac{(1+0.1)^{3}-1}{0.1 \cdot(1+0.1)^{3}}\right]+\frac{140,000}{(1+0.1)^{3}}](/images/math/7/4/4/7447c8d29d43cf732fe492ae063c01ca.png)
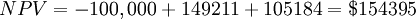
NPV of a perpetuity
For the special case that, 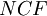 is considered as perpetuity, which is given for an infinite and constant stream of identical cash flows the NPV can be expressed as follows [1]:
is considered as perpetuity, which is given for an infinite and constant stream of identical cash flows the NPV can be expressed as follows [1]:
Example:
A company decides to invest $100,000 for a project which is expected to give a net cash flow of $60,000 in perpetuity with a discount rate of 10%. Calculate the NPV.
Using The NPV of a perpetuity formula,
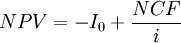
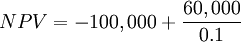
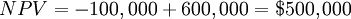
Decision rule
Net present value is used to assess the attractiveness of the investment and it shows how much value an investment or project adds to the firm [2].
| Condition | Idea | Decision |
|---|---|---|
| If NPV > 0 | Investment increase the value (profit) of the company in the amount of the net present value. | Investment can be accepted. |
| If NPV = 0 | The investment just returns the cost of capital. No increase or decrease in wealth results. | This project adds no monetary value. Difficult to get the decision whether to accept or reject the project. Decision should be based on other criteria. |
| If NPV < 0 | An implementation would destroy value (profit) in an amount equal to the negative NPV. | The investment can be rejected. |
As a summary, the following two profitability criteria must be met for the economic viability of an investment [2]:
Absolute profitability: The net present value of an investment option must be positive or at least zero (NPV≥ 0).
Relative profitability: The option with the highest positive NPV is the most profitable and usually the preferred option, provided that the investment risk is the same.
Applications
NPV can be used to evaluate the financial viability of different types of investments [4].
- Independent Projects:
The acceptance or rejection of one project does not directly eliminate other projects from consideration or cause the likelihood of their selection.
Example:
A company has an opportunity to invest in the construction of a new product line and at the same time the replacement of a machine currently used to produce one of its products.
| Now | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | NPV | |
|---|---|---|---|---|---|---|---|
| Construction of a new product line | -$1,000,000 | $75,000 | $275,000 | $450,000 | $500,000 | $525,000 | $198,350 |
| Replacement of a machine | -$1,000,000 | $600,000 | $575,000 | $75,000 | - | - | $250,000 |
Since both NPV > 0, the company can accept the investment in both projects since it has the ability to invest in both.
- Mutually Exclusive Projects:
The acceptance of one prevents the acceptance of an alternative proposal. That is, two or more projects cannot be pursued simultaneously. The selection of one will exclude the acceptance of the other. The NPV method can be used to select between mutually exclusive projects; the one with the higher NPV should be selected.
Example:
A company has a block of land, which can be used to establish a food manufacturing business or a steel fabrication plant.
| Now | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | NPV | |
|---|---|---|---|---|---|---|---|
| Food manufacturing business | -$5,000,000 | $4,000,000 | $1,000,000 | $800,000 | $600,000 | $300,000 | $489,590 |
| Steel fabrication plant | -$5,000,000 | $1,000,000 | $1,000,000 | $1,900,000 | $2,200,000 | $2,300,000 | $745,660 |
Even though both projects give positive NPV, the company cannot invest in both since they are mutually exclusive. Therefore it has to select the project which gives the highest NPV. In this case it is the steel fabrication plant.
- Contingent Projects:
The acceptance or rejection of one is dependent on the decision to accept or reject one or more other projects. Contingent projects may be complementary or substitute. For Example, The decision to start a pharmacy may be contingent upon a decision to establish a doctor's surgery in an adjacent building. The cash flows of the pharmacy will be enhanced by the existence of a nearby surgery and vice versa.
Limitations
- NPV calculation is based on several estimates such as future cash flows and discount rate, therefore there is a high chance for errors that can drastically affect the end result of the calculation. Since every project has a unique set of processes there is lots of room for errors in estimating cash flows and the actual figures can have great variance. NPV often takes an optimistic approach to future cash flow calculations by overestimating benefits (incoming cashflows) and underestimating costs (outgoing cashflows). These problems can be mitigated by double-checking estimates, performing sensitivity analysis or Monte Carlo analysis after doing the initial calculations [8]. On the other hand, Investment decisions based on the NPV method are highly sensitive to the selected discount rate. Using a discount rate that is too low will make suboptimal investments and using too high will result in rejecting good investments. Moreover, the NPV is calculated based on the assumption that the discount rate remains the same throughout the life of the project. Therefore, it does not account for the fluctuation of discount rates according to the market situation [4]. To remove this limitation NPV can be calculated using variable discount rates if they are known for the duration of the investment [1].
- The NPV is expressed in absolute terms rather than a relative term. Therefore it does not useful for comparing projects of different sizes as the largest projects typically generate the highest returns [4]. The size of the NPV output is determined mostly by the size of the input. A higher NPV does not necessarily mean a better investment. If there are two investments or projects up for decision, and one project is larger in scale, the NPV will be higher for that project as NPV is reported absolute terms and a larger investment will result in a larger NPV number. It is important to assess the returns from an investment in percentage terms to get an accurate picture of which investment provides a better return.
- It does not consider the non-cash benefits generated from a project into consideration while making decisions. NPV method is purely quantitive in nature and does not consider qualitative factors. Some elements of the costs and benefits of the projects are not quantitative, so there is great difficulty in taking them into consideration. NPV method gives financial feasibility of different projects, but often, other qualitative factors exist that must be considered.
Annotated Bibliography
Häcker J. and Ernst D., Ch. 8 - Investment Appraisal. In: Financial Modeling. Global Financial Markets(2017), pp.343-384
The investment appraisal chapter in Financial modeling book by Häcker J. and Ernst D. introduces the concept of investment appraisal and provides a good overview of methods and approaches in investment management. The book introduces the static & dynamic approaches of investment appraisal and provide a comprehensive discussion on different methods under each approach & describe why dynammic approaches such as NPV, IRR are superior than the static approaches like payback. The writers introduce the net present value as one of the main methods of dynamic approach and it clearly describes the NPV calculation method and the importance of underlying variables of NPV formula. The book was the ideal source to provide a good explanation of the concept of financial appraisal, the concept of NPV, how to calculate NPV & its applications. Also, this was useful to get idea about the other methods such as payback, IRR etc.
Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models (2018), pp. 85-114
Chapter 5 of Economic role of transport infrastructure: Theory and models book by Ferrari, C., Bottasso, A., Conti, M. and Tei, A. introduce the importance of investment appraisal in large projects such as transport infrastructure. It critically highlights the different financial appraisal methods and it especially highlights the importance of Net present value in the context of large projects. Especially it points out the relationship of discount rate & time period with NPV and the importance of selecting the correct discount rate when the projects are appraised based on net present value. It provides different approaches to determine the discounting rates. This chapter also highlights the NPV calculation method & how to treat when project are mutually exclusive. Additionally it introduces the importance of performing sensitivity analysis when calculating NPV. This is a good reference to get overall picture behind the financial appraisal methods and its applications.
Poggensee K. and Poggensee J., Ch. 3 - Dynamic Investment Calculation Methods. In: Investment Valuation and Appraisal (2021), pp. 85-140
The book Investment Valuation and Appraisal by Poggensee K. and Poggensee J. was a useful reference to get a thorough idea about the appraisal of projects using different financial appraisal methods. Chapter 3 of this book introduces the dynamic investment appraisal methods such as net present value, Internal rate of return, annuity method, etc. It critically argues the assumptions of dynamic investment appraisal methods. It highlights the net present value as the most widely used method in the dynamic approach and introduces the NPV and discounting concepts. This was a good source to get the idea of discounting where projecting the future net cashflows into present time and NPV calculations based on different scenarios such as annuity, perpetuity etc.
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 Häcker J. and Ernst D., Ch. 8 - Investment Appraisal. In: Financial Modeling. Global Financial Markets, (Palgrave Macmillan, London, 2017), pp. 343-384, https://doi.org/10.1057/978-1-137-42658-1_8
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models, (Elsevier, 2018), pp. 85-114, https://doi.org/10.1016/C2016-0-03558-1
- ↑ 3.0 3.1 3.2 3.3 3.4 Žižlavský, O., Net present value approach: method for economic assessment of innovation projects. Procedia-Social and Behavioral Sciences, 19th International Scientific Conference, Economics and Management, 156 (2014), pp. 506-512.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Bora, B., Comparison between net present value and internal rate of return, International Journal of Research in Finance and Marketing, (2015), 5(12), pp.61-71
- ↑ Ing E. and Lester A., Ch. 5 - Business case and Ch. 6 - Investment Appraisal. In: Project Management, Planning and Control. 7th Edition, (Elsevier, 2017), pp. 25-36, https://doi.org/10.1016/B978-0-08-102020-3.00006-1
- ↑ 6.0 6.1 Konstantin P. and Konstantin M., Ch. 4 - Investment Appraisal Methods. In: Power and Energy Systems Engineering Economics, (Springer, Cham, 2018), pp. 39-64, https://doi.org/10.1007/978-3-319-72383-9_4
- ↑ 7.0 7.1 7.2 Poggensee K. and Poggensee J., Ch. 3 - Dynamic Investment Calculation Methods. In: Investment Valuation and Appraisal, (Springer, Cham, 2021), pp. 85-140, https://doi.org/10.1007/978-3-030-62440-8
- ↑ 8.0 8.1 LOCK, D., Project management. 10th edition, (Farnham, Surrey, England, Gower Pub., 2013).
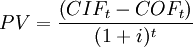
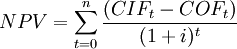
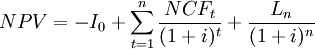
![N P V=-I_{0}+N C F \cdot\left[\frac{(1+i)^{n}-1}{i \cdot(1+i)^{n}}\right]+\frac{L_{n}}{(1+i)^{n}}](/images/math/f/b/b/fbb9818d6744581d2a9ff5023d8e9138.png)