Game theory in project management
Introduction
In order to advance, management and more specifically strategic management, needs to integrate other scientific disciplines in its own concept. Game theory is an aspect of mathematics designed to understand, model and predict the behaviour of actors considering a determined environment. Basically, the theory identifies the players, their assets and their possible strategies. It simulates, through a precise defined game, the different interaction between entities such as companies, states, lobbies, individuals etc. The concept is already widely used in many fields such as psychology, economics, politics and others. Despite its great efficiency, some prerequisites of Game theory may seem contradictory with a management point of view. First, the extreme mathematical complexity needed to treat some problems is an important limitation, secondly the presumed rationality of the players can be defected in the real world.
Regarding some simple games, such as the prisoner dilemma, this article focuses on the possible outcomes of Game theory leading to development of models and decision making process in management. Going through different scenarios and examples while considering the ethical point of view, this article outlines the use of Game theory as a simple tool. It opens a new and more rational perspective for the manager which can be used in addition to usual managerial skills.
Contents |
The concept
Overview
Game theory is, at first, a mathematic discipline based on a very high formal demands. This article will not try to explain this aspect. Therefor it has to be considered has an introduction of the concept of game theory and its possible outcomes regarding project management.
Game theory main goal is to help to achieve successful decision making process. In order to achieve these objectives the situation has to be studied in a very precise and special framework. This framework is destined to modulate a game, the more the situation can easily be assimilated as such, the more the theory will be effective. The translation from a real world situation to a game is done through high mathematical formalism. Moreover, the framework also requires to identify the payoff each player is looking for and a set of rules. Most of the rules can be determined regarding the situation, others are inherent to game theory, that is:
- The players act rationally.
- The players act egoistically.
The target is always to optimize one’s own payoff. To do so it is however important that the player do not only consider the different strategies available to himself but anticipates the optimal strategy of the other players in order to predict their choices. In most of the games, the payoff depends on strategies of others and therefor the concept of reciprocal influencing plays a huge part in the way the game is played.
Different types of game can be identified regarding the basic settings.
For examples games can be symmetric, meaning that both players start the game with equal settings and possibilities, or asymmetric meaning that the choice of the same strategies won’t lead to the same outcomes for the players. One can be considered as having an advantage.
Games can also be cooperative: the players can create alliances and communicate. We can also chose to decide if players are aware of what the others are doing to simulate real-life situation. Finally we have zero-sum game where each players play alone regarding its own best interest. The payoffs are fixed to a certain value, and a player winning mean that others have to lose. For example we can consider a cake cut in different parts. If one player take a big part, then the other will automatically get less payoff i.e. less cake regarding our example. No cooperation or alliances can ever change this outcome, the game is defined as being strictly competitive.
In opposite in non-zero-sum game, gains from one player doesn’t imply losses for an other one. The amount of gain possible is not fixed.
First example : The prisoner's dilemma
First, let’s present the most famous example of Game Theory: the prisoner’s dilemma.
The prisoner’s dilemma is a simple non-zero-sum and non-cooperative game. Players can’t communicate.
We will use this example to explain some general notion of game theory:
The dominant strategy: the best strategy regarding the payoff and regardless what the others players are doing. First, let’s notice that the prisoner’s dilemma is a symmetric game. Let’s now consider Player 1: if he confesses and P2 Confesses he gets 8 years, if he doesn’t confess and P2 confesses he takes 15, so confessing is better.
Again if P1 confesses and P2 doesn’t he takes 2 years and if P1 doesn’t confess and P2 doesn’t confess P1 takes 3 years so confessing is better.
Regarding what Player 2 is doing confessing gives better outcome for P1, therefor it is the dominant strategy.
The Nash equilibrium: A Nash equilibrium is defined as a solution where no player can increase its payoff by moving away from it.
Let’s consider the prisoner’s dilemma again:
Let’s start with the combination 2 (P1 confess and P2 doesn’t). Considering that P2 doesn’t confess, should P1 not confess? No he will take 3 years instead of 2. On the other hand P2 should change his choice i.e. confess in order to get 8 years instead of 8, therefor it is not a Nash equilibrium.
In combination 4, both players can increase their outcome by confessing so this is not a Nash equilibrium either. Combination 3 is symmetric to 2.
Let’s consider our dominant strategy, 1: if one of the two players decide to change his strategy he will take 15 years instead of 8 years. Therefor there is no reason to change and in this particular case the dominant strategy is also a Nash equilibrium.
Therefor the outcomes 2, 3, 4 should never happened if the players play regarding their own best interest. Of course we immediately notice that the combination 4 will be better for both players. But regarding the rules (no communication and no information about what the others players is doing), the only possible outcome is 1 (the players acting rationally and egoistically).
The prisoner’s dilemma is a basic game, however it is really useful to understand the concept of the theory and its possible applications regarding decision-making.
The complexity of modelling real life situation through game theory is virtually unlimited. However the mathematical formalisation become more and more complex at the same time. In theory it is possible to model games with infinite players and set as many rules as needed in order to represent reality: the game can be sequential or non-sequential, the information available can be complete or not, players can be able to communicate, to form coalition…
Application and use
The need to take strategic behaviour into account
Strategic behaviour should be taken into account when the stakes are high, if game theory outcome are not always shaped to reality, then people thinking through game theory’s basis won’t act as we could expect or desire in reality. Therefor one should always take into account the possibility of pure strategic behaviour from one or several elements. Then, a manager have to be aware of this different way of thinking in order to choose and enforce the best strategy to achieve its goals.
For one example when organizers have failed to implement effective rules, we can consider the London Olympics in 2012 and more specifically the badminton teams.
The tournament consists in 2 phases:
Phase 1: 16 teams, 4 groups of 4 teams and the best 2 teams of each group advanced.
Phase 2: 8 teams, immediate elimination.
What creates the issue is that the Danish team made a huge upset defeating one of the Chinese team WC, considered to be by far the strongest one. Therefor QW advanced 2nd of its group to the phase 2.
The problem can be defined as a misalignment between what the Committee desired to create and what the athletes wanted. The Committee wanted great and fair games, the athletes wanted to win the best medal possible.
After the defeat of QW, it happens that in the last day of Phase 1, two others matches go wrong. It appears that in both matches the winner would meet QW in semi-final, whereas the loser would only meet them in final in the Phase 2 of the tournament (all the teams would reach Phase 2 no matter the issue of these specific matches). Considering that everyone believed that QW was stronger than any other teams, all 4 teams in both matches tried their best to…lose.
From a game theory point of view, the behaviour of the teams is perfectly logical and understandable. They chose their strategy, in this case losing, in order to optimized their possible outcomes (getting the best medal possible) and taking into account the frame of the game (meaning they tried to meet QW the latest possible, the team being considered as unbeatable).
Here is a short video showing a part of one of the matches.
Even if the comportment of the players can be put into question (indeed, the teams have been excluded from the tournament) they never broke any explicit rules. Actually one could say they act rationally and egoistically.
Agreement game
As a managerial point of view, game theory is a very good tool to get into others people shoes and try to fully understand their point of view and their options. With a game theory vocabulary, we can say that the main goal is to fully understand all the strategies available for all the players. Then the model can help to choose the best strategy in order to maximise one’s own profit, or a coalition profit, or just chose the best reply in order to defeat the opponent in zero-sum game.
However some situations can be directly treated trough game theory. I’ll now present some simples examples where game theory can model a management issue and bring a satisfying solution.
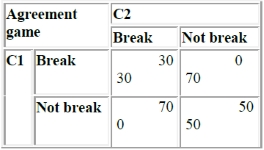
For example we can model an agreement between 2 companies considering a precise market.
Let’s say that company 1 C1 and company 2 C2 agreed to share a market and release a certain amount of a product P in order to keep the price high. If C1 and C2 keep the agreement they sell P at 50. If one break the agreement, we will assume that he will be able to win on the long term the entire market and therefore sell the product to a higher price: 70. If they both break the agreement and try to increase their sells, there will be an overproduction of P, the market will saturate and the price will go low: 30. We can represent this game through a table:
It is interesting to see that the Nash equilibrium in this situation consists in C1 and C2 breaking the agreement. However it put them in a situation less favourable than keeping the agreement intact.
Nevertheless such a situation is instable because the possible outcome in breaking the agreement is really attractive. Such a situation will require an extra set of rules to maintain the most profitable outcome for both companies. In reality it means an authority able to guarantee the respect of the agreement (contracts, etc….).
One can also simply consider that truth between the companies can be enough, but such a thing as truth doesn’t exist according to the basics rules of Game Theory. We will consider this aspect more precisely at the end of this article.
Market entry game
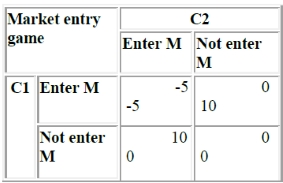
Keeping the model of the prisoner’s dilemma we can think of a game simulating the entry in the market of a new product.
Let’s consider two companies C1 and C2, sharing a market M. In order to keep it simple let’s say that they intend to sell exactly the same product P, and will both be as good as selling it. The cost to develop P is 20.
M represents a total value of 30.
Therefore, if both enter the market at the same time, they will both lose money, the cost of production being higher than the expected benefit coming from the exploitation of 1/2 M. If one doesn’t enter the market he won’t have any production cost, but also won’t be able to make profit out of the product.
This is a simultaneous competitive game. We can model him through a table similar to the prisoner’s dilemma:
We can easily see that the top right and the bottom left cases are both Nash equilibrium, meaning that both companies have no interest to change their strategies if a Nash equilibrium happens.
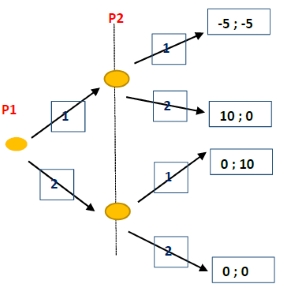
Through this model we can also consider another aspect of games, the first move advantage (FMA). If we consider this game as sequential (and therefore abandoned the simultaneous part), we can highlight the fact that the market entry game presents a FMA.
Let’s consider:
- 1: enter the market
- 2: doesn't enter the market
In the figure you can see the same game represented as sequential, meaning one player chose its strategy first and the other has to reply afterwards.
We now clearly see that is P1 has the opportunity to make the first move he will surely enter the market i.e. chose 1. Then P2 has no choice but to not enter the market in order to reduce its loss. P1 ends up with the best outcome possible; a benefit of 10.
Coalition game
Finally let’s consider a more complicated game based on coalition. It suits better the environment of companies but also requires more formalism.
We can consider the development of a new cd format (BLU RAY for example) which will oppose to a former or competitive one: High Quality DVD.
In order to achieve a full product, a cd company constructor (hardware i.e. lectors) and editors (cd producers: movies, games) are needed.
We call consortium the association of cd companies and editors who have chosen the same format i.e. the same product. In order to simplify, we’ll also assume that the size of the consortium has a direct impact on the benefit he may realize: the bigger the stronger and the better.
In another hand we should also consider that the redistribution of the overall benefits inside the consortium will decrease with the number of participants i.e. with the size of the consortium.
We define:
- N, the total amount of companies.
- n, the amount of companies in one consortium.
- T the total amount of benefit expectable in the entire market.
- B(x,y) the benefit of a consortium of x constructors and y editors . The other will have T-B.
- α the part of the market wins by one consortium (the other would have 1- α).
Therefore the Profit P realised by one constructor in a consortium is:
P= α*B/n
We will consider a low amount of companies (4 and 4) in order to simplify the formalism of the game. 1/1/1/1 means that all the companies (editors or constructors) have chosen the format 1.
Their benefits is therefore:
P= α*(B(4,4))/4
We can then evaluate if the situation is susceptible to move or not regarding the different values and scenario.
If one constructor decide to leave the consortium for the other format and get an editor with him then we have:
1/1/1/2 and two types of profit:
P1= α*B(3,3)/3 P2=(1-α)*(B(1,1))/1
The situation is stable for the consortium 1 if P1 ≥ α*(B(2,2))/2 et P1 ≥ α*(B(2,3))/3 etc…
For the consortium 2, the stability is given by (1- α) B(1,1) ≥ α*(B(3,4))/3 , it means that the editor have a better outcome by staying with the constructor who have chosen 2.
This example quite simple, shows that Game theory is able to model complex interactions between companies and to represent different types of real life situation such as the need to create alliances in order to survive.
Limitations
- Never ending games: The Cake sharing issue.
Let’s consider 3 people who wants to share a cake. The decision process is democratic, if a majority agrees, the 3rd one have no choice.
Let’s call 1, 2 and 3 the players.
We rapidly see a cycle appears, all the strategies are dominated by others. The game will never end regarding game theory, car 1 player can always make a proposal which will suits better to two players.
- The concept of rationality are also very often in contradiction with real life comportment.
Let’s consider for example the dictator game:
One player decide to give a % of a sum to another player, and this one has to accept (passive player).
Considering 100 the sum, the player should give 0 and keep 100. But studies have shown that people often decides to give some money to the other player, often 40.
In another version of the game, the player 2 have to decide if he accepts the donation, or refuses. In the last case, no one get money.
In Game theory even a 99/1 repartition should be accepted, because player 2 still optimizes his outcome by accepting. However, these types of offers are very often rejected. It is therefore necessary to consider concept such are punishment, rewards, equity. These are very important in order to simulate human behaviour, but are not included in Game theory.
- Another limitation of Game theory already mentioned is the mathematical complexity that is rarely accessible for most.