Project viability assessment through Net Present Value (NPV)

Abstract

The Net Present Value (NPV) is a widely used financial metric in project management. Its purpose is to evaluate the profitability of a proposed project by aggregating the streams of costs and benefits into a single value. This makes for an effective indicator of identifying profitable projects when assessing multiple projects at a time. For a given project to be considered a profitable investment, its NPV must be larger than zero.

Central to the calculation of the NPV is assigning varying weights, dependent on time, to the benefits and costs through the utilization of a so-called discount factor, which is calculated using a discount rate. The discount rate represents the rate of interest that is used to discount all future costs and benefits. By incorporating this principle, the NPV accounts for and subscribes to the paradigm of the time value of money, referring to the idea that money has a different value at different points in time.

This article explores central concepts connected to the calculation and application of NPV in the assessment of projects, programs, or portfolios. Moreover, how it relates to financial appraisals of projects and how it can support decision-makers in the process of doing so. For demonstration purposes, an example of the calculation of an emulated project's NPV will be given. Moreover, the advantages and disadvantages of using NPV as an indicator of project profitability will be addressed.

NPV Formula

The net present value achieves comparability of all costs and benefits by discounting them to the beginning of the investment period. The NPV is amongst the most frequent and sophisticated tools when it comes to assessing the profitability of projects and investments. The formula used to calculate the net present value is presented below:

$NPV = \sum_{t=0}^{N}\frac{B_t-C_t}{(1+r)^t}$

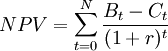
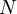• $N$:The calculation period of the project in years.

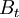• $B_t$: The aggregated amount of benefits (both positive and negative) in year t

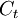• $C_t$: The amount of investments costs in year t

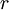• $r$: The discount rate

There are two inherent principles to the NPV as a tool. The first principle is the time value of money, which postulates that an uncertain Danish Crown tomorrow is less valuable than a Danish Crown today. This is modulated by the use of the discount factor 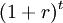$(1+r)^t$, where a discount rate is used.Therefore, the NPV achieves comparability of the costs and benefits that happen at different points in time by determining their present values by discounting them to 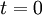$t = 0$. The second principle considers all future costs and benefits affiliated with the project or investment. The project’s worth is evaluated by assessing its ability to generate economic value in the specified time horizon, 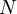$N$..For a given project assessed, the streams of costs and benefits are aggregated into a single number, the NPV index value. This allows for quick and effective comparisons of projects, programs, and portfolios. The NPV index value, used as a proxy of the future benefits from commencing the project, can be estimated as either zero, negative, or a positive number, with the positive number serving as an estimate of the project’s potential long-term value. This makes for a

Time value of money

Brief explanation time value of money and how it relates to NPV

Discount rate

Figure 1: Discount factor versus discount rate. The discount factor as a function of t and the discount rate r. Inspiration drawn from.

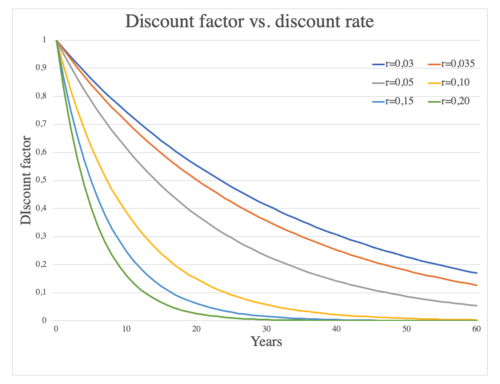
The discount rate is the interest rate used to convert future cash flows into an equivalent one-off upfront sum or present value . As the discount rate increases, the lower the present value of a given future amount becomes. Hence the magnitude of the discount rate exerts a significant influence on the net present value. For instance, if the selected discount rate level is set too high, it may make potentially good projects, programs or portfolios seem unattractive, whereas if set too low, it might result in the opposite.

The selection of an appropriate discount rate can be a very exhaustive and challenging task, as the decision is dependent on multiple factors, to name a few:

• The situational circumstances under which the investment project is taking place are characterized by fundamental uncertainty, computable risk, or certainty. The first, driving the discount rate to increase the most. Furthermore, the jurisdiction and location of the project being commenced also play a role in the choice of a discount rate. (See EU reference)
• The duration of the time horizon, especially in a socio-economic context, numerous countries have opted to differentiate between projects that span less than or more than 30-50 years, with the latter receiving a lower discount rate.
• Private versus public and government bodies. Discounting from a firm’s or individual perspective is inherently different than that of government bodies.

In relation to state-aided projects, the European Commission calculates and issues base rates each month for countries within the union. The discount rate can be found by adding a margin of a 100 basispoints to the base rate. The base rate for the first four months of 2023 is depicted in table 1.

Table 1: Base rates from the European Commission.

Base rates as of 1.4.2023
From	To	AT	BE	BG	CY	CZ	DE	DK	EE	EL	ES	FI	FR	HR	HU	IE	IT	LT	LU	LV	MT	NL	PL	PT	RO	SE	SI	SK	UK
1.4.2023	…	3.06	3.06	1.51	3.06	7.43	3.06	3.54	3.06	3.06	3.06	3.06	3.06	3.06	15.10	3.06	3.06	3.06	3.06	3.06	3.06	3.06	7.62	3.06	8.31	3.21	3.06	3.06	3.52
1.3.2023	31.3.2023	3.06	3.06	1.10	3.06	7.43	3.06	2.92	3.06	3.06	3.06	3.06	3.06	3.06	15.10	3.06	3.06	3.06	3.06	3.06	3.06	3.06	7.62	3.06	8.31	2.96	3.06	3.06	3.52
1.2.2023	28.2.2023	2.56	2.56	0.79	2.56	7.43	2.56	2.92	2.56	2.56	2.56	2.56	2.56	2.56	15.10	2.56	2.56	2.56	2.56	2.56	2.56	2.56	7.62	2.56	8.31	2.44	2.56	2.56	2.77
1.1.2023	31.1.2023	2.56	2.56	0.36	2.56	7.43	2.56	2.92	2.56	2.56	2.56	2.56	2.56	2.56	15.10	2.56	2.56	2.56	2.56	2.56	2.56	2.56	7.62	2.56	8.31	2.44	2.56	2.56	2.77

The weighted average cost of capital (WACC) is another way to determine and select an appropriate discount rate for firms, in the appraisal process of a proposed investment or project using the NPV. The WACC represents the risk to the future cashflows received by an organization from its operations including equity and debt. It weighs the cost of each capital source by its relevant weight by market value and adds it together to determine the total. The gist of using the WACC besides it representing a minimum rate of return that a firm must achieve is that it can be used as a proxy for a suitable discount rate . The WACC is calculated as follows:

$WACC = (\frac{E}{V}\cdot Re)+(\frac{D}{V}\cdot Rd \cdot (1-Tc))$

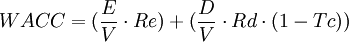
Where

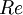• $Re$: Cost of equity
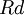• $Rd$: Cost of debt
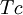• $Tc$: Corporate tax rate
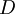• $D$: Market value of the company's debt
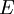• $E$: Market value of the company's equity
• $V$ = $D+E$

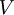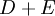
To summarize, the choice of discount rate has a tremendous impact on the appraisal outcome of investments or projects using the NPV. To a high extent, the selection of the discount rate is dependent on the context in which it is used. Therefore, one must be aware of the circumstances, the type of project, and the affiliated risk that the very project or investment comes with. In its most basic shape, the discount rate simply gives an insight into how profitable a future project or investment can be for a particular organization.

Financial Appraisal

The gist of financial appraisals is to deliver the maximum value for money of a project for the project implementor. Moreover, to determine the viability of the investment or project by assessing the future net cash flow as a result of the realization. The financial appraisal is a systematic process for analyzing alternative uses of limited assets and resources. It focuses on the assessment of benefits, costs, objectives, risks, funding, and executability. The financial appraisal facilities great management practices and it is vital to create transparency, and accountability, and make informed decisions. Financial appraisals are a difficult matter, yet an important tool, even an imperfect one, that makes it possible to compare options on a project, program, and portfolio level. It can be complemented by a business case, that takes the wider narrative into account on how that said investment could be executed to realize the intended benefits. There are plenty of tools to choose from besides the NPV, the common nominator being comparability, such as the

• Internal rate of return (IRR),

• Cost-benefit analysis (CBA),

• Multiple-criteria decision analysis (MCDA).

Each tool provides unique insights into the profitability of an investment or project and can be applied in conjunction to provide a more comprehensive understanding. Doing so might uncover possible clues to improve the investment or project itself as well as the financial appraisal.

Application and decision making

In the following paragraph, the application of NPV in regard to assessing the profitability of a project prior to commencing it will be outlined.

Example

A practical example on how to calculate the NPV of a construction project.

Annotated Bibliography

Ferarri, C., Conti, M., Bottasso, A., & Tei, A. (2019). Economic Role of Transport Infrastructure: Theory and Models. In Elsevier. https://doi.org/10.1016/b978-0-12-813096-4.01001-5 Chapter 5 of the book gives a thorough introduction to the theory and models of financial appraisals. It provides the necessary framework for executing appraisals and provides a comprehensive understanding of the net present value, Internal rate of return, discount rate, and Cost Benefit Analysis.