MCDM-APH method in decision making
Developed by Mansoor Samadi
The MCDM-APH (Multi-Criteria Decision Making - Analytic Hierarchy Process) is a tool that makes complex decisions. MCDM is a systematic approach that evaluate conflicting criterias in decision making, one of these approaches is APH which uses a mathematic method to derive a relative importance of criteria in a decision problem.
The method was developed in the 1970s by Thomas Saaty [1], AHP is a mathematical method that is used to derive the relative importance of criteria in a decision problem. The idea behind the method is that a decision problem can be represented as a hierarchical structure, with the most important criteria at the top followed by the lesser important criteria at the bottom.
Decision-making is at the core of project management and yet it can be a daunting task, especially when the projects are complex and multi-facted projects. The pressure of making decisions in a timely and informed manner can be compounded when the criteria for success is not defined clearly, At time like this it not unusual that project managers may feel overwhelmed and unable to determine the most important factors to consider. This is where the APH-decision-making method provides a systematic approach to this challenge. This approach is addressing the complexity of decision making by Segmenting the process into manageable chunks. By following these steps the project manager can get a obtain a holistic view of the project's key performance indicators and success factors.
Contents |
APH for Project management
A project manager in the current day is faced with a dynamic environment, where making the right choices based on fitting objective is a crucial factor for weather a organization is profitable or not. Simply completing a project and hope for the best outcome is no longer enough, as the projects are more complex with more risks and dynamic challenges this means that there is a higher demand for a strategic approach.
In order to accomplish this, organizations are using more resources in portfolio management which helps them structurize the projects so they are in alignment with the organizations strategic goals. One of the main part of portfolio management is cost-benefit, where projects with high benefits is given higher priority. The analysis takes into account the benefits of completing a project as well as the cost, as projects become more complex the cost-benefit analysis becomes as complex and hectic.
Here are three exampels on where the APH method is applied for project, portfolio and program management.
-Project selection
-Risk assessment -------------------------------------
-Resource allocation
- Picking suppliers Across industries the AHP method have been used in selecting suppliers such as the automotive industry, construction and green supply chain management[2] [3] [4]. There have been multiple papers that demonstrate the effectiveness of the AHP method in supplier selection. With the AHP method it becomes easier to minimize supplier-related risks such as financial stability, quality control, and delivery reliability. The method can also be used to rank the supplier performance over time and adjust changes.
The analytic hierarchy process
Assuming that we have multiple criterias and alternatives, the weight of the criterias is first weighted using pairwise comparison, using saatys scale:
| The foundation scale of absolute numbers | ||
|---|---|---|
| Intensity of importance | Definition | Explanation |
| 1 | Equal importance | Two activities contribute equally to the objective |
| 2 | Weak or slightly | |
| 3 | Moderate importance | Experience and judgment slightly favor one activity over another |
| 4 | Moderate plus | |
| 5 | Strong importance | Experience and judgment strongly favor one activity over another |
| 6 | Strong plus | |
| 7 | Very strong | An activity is favored very strongly over another, its dominance demonstrated in practice |
| 8 | Very, very strong | |
| 9 | Extreme importance | The evidence favoring one activity over another is of the highest possible order of affirmation |
| Table 1: Saatys scale [6] | ||
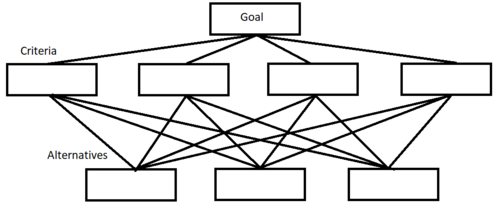
The APH method makes use of the hiracy approach, where the objective is at the top and criteria is below it and the alternatives are at the bottom.
Example for AHP
NOTE TO ME:------------------------------------------------------------ NEED INTRO
- Identify the objectives
- Assign weights to the criteria by performing pairwise comparisons
- Evaluate the performance of each alternative with respect to each criterion
- Preform Consistancy test
- Calculate the global priority of each criteria and ranking
Idenrify the objective
A company is in the process of implementing a PMO system and is considering 3 providors. The company have come up with three specific criteria, which are considered highly important when determining which product they should buy. These criteria are cost, technical support, and flexibility.
Assign weights to the criteria by performing pairwise comparisons
When the objective is identified and relevent emperical information is gathered, the next step is to determin the relative importance among the criteria that is under consideration. This process involves giving a specific weight to each criteria based on its percieved importance. This step establish a hierachy, it ensures that the most significant criteria is given appropriate attention. This is done by giving each criteria a relative importance in the Saatys scale 1-9 as shown in table 1, which a person decides. It should be noted that the sum of each row is computed, this is used for later calculations.
| Cost | Support | Flexibility | |
|---|---|---|---|
| Cost | 1,00 | 2,00 | 3,00 |
| Support | 0,50 | 1,00 | 2,00 |
| Flexibility | 0,33 | 0,50 | 1,00 |
| Sum | 1,83 | 3,50 | 6,00 |
Evaluate the performance of each alternative with respect to each criterion
The alternatives are assesed by making a pariwise comparision, just like the previous step. For this step the alternatives are compared against eachother with respect to each criterion the, where they are given a relative importance just like earlier, which a person decides. they are then compiled into tabels, shown below:
| Alternatives with respect to cost | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 7,00 | 2,00 |
| Company 2 | 0,14 | 1,00 | 0,25 |
| Company 3 | 0,50 | 4,00 | 1,00 |
| sum | 1,64 | 12,00 | 3,25 |
| Alternatives with respect to support | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 5,00 | 3,00 |
| Company 2 | 0,20 | 1,00 | 0,50 |
| Company 3 | 0,33 | 2,00 | 1,00 |
| Sum | 1,53 | 8,00 | 4,50 |
| Alternatives with respect to flexibility | |||
|---|---|---|---|
| Company 1 | Company 2 | Company 3 | |
| Company 1 | 1,00 | 0,11 | 0,13 |
| Company 2 | 9,00 | 1,00 | 1,00 |
| Company 3 | 8,00 | 1,00 | 1,00 |
| Sum | 18,00 | 2,11 | 2,13 |
In order to give a relative weight to each criterium, the matrices are normalised. This is done by dividing each value with the sum of the column value. Afterwards the priority is calculated, this is done by taking the sum and dividing with the number of elements, 3 in this case:
| Criteria Normalised | ||||
|---|---|---|---|---|
| Cost | Support | Flexibility | Priority | |
| Cost | 0,55 | 0,57 | 0,50 | 0,54 |
| Support | 0,27 | 0,29 | 0,33 | 0,30 |
| Flexibility | 0,18 | 0,14 | 0,17 | 0,16 |
The values calculated under priority have a meaning in AHP, the values represent the relative importance of the criteria to the overall goal. In this case the company have decided that flexibility have a importance of 16% (this is the priority calculated in the above table).
Preform consistancy test
When preforming the consistancy the following is computed:
- The largest eigenvalue, λ_max, of the matrix is calculated
- The Consistency index (CI) and the consistency ratio (CR) is calculated
Math software, like maple, was used to find the largest eigenvalue of the matrix. The consistency index is calculated with the following formula:
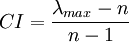
where n is the number of elements. RI is is called the random consistency index, to finx the consistency ratio the CI is divided by the RI. The consistency ratio can be calculated with the following expression:
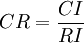
The values for RI is presented below:
| Consistency of random matrices | |||||
|---|---|---|---|---|---|
| matrix order | 1 | 2 | 3 | 4 | ... |
| RI | 0.00 | 0.00 | 0.52 | 0.89 | ... |
The consistancy test is preformed for the criterum matrix,cost matrix, support matrix and flexibility matrix:
| Consistancy test | ||||
|---|---|---|---|---|
| Criterium | Cost | Support | Flexibility | |
| Lambda_max | 3,009 | 3,002 | 3,004 | 3,002 |
| CI | 0,004 | 0,001 | 0,002 | 0,001 |
| CR | 0,008 | 0,002 | 0,003 | 0,001 |
Calculate the global priority of each criteria and ranking
| The AHP ranking | |||||
|---|---|---|---|---|---|
| Cost | Support | Flexibility | Global Priority | Rank | |
| Company 1 | 0,602 | 0,648 | 0,056 | 0,526 | 1 |
| Company 2 | 0,082 | 0,122 | 0,481 | 0,160 | 3 |
| Company 3 | 0,315 | 0,230 | 0,463 | 0,314 | 2 |
https://www.pmi.org/learning/library/analytic-hierarchy-process-prioritize-projects-6608#
Critique of the AHP method
NOTE TO ME: look here[7]
Inplementation of AHP method in organisations
NOTE TO ME Look at the conclusion[6]
References
- ↑ Saaty, T. L. How to make a decision: The analytic hierarchy process. European Journal of Operational Research, 48(1), 9-26, 1990. https://www.sciencedirect.com/science/article/pii/037722179090057I
- ↑ Wang, Y., Dong, Y., & Hao, J. (2018). AHP-based supplier selection for an automotive manufacturer in China. Journal of Manufacturing Systems, 46, 63-70.
- ↑ Chan, A. P., Chan, D. W., & Ho, K. S. (2016). Application of AHP in selecting suppliers for a construction project in China. Journal of Construction Engineering and Management, 142(6), 04016012.
- ↑ Chai, J., Liu, J., & Lu, Y. (2017). An AHP-based evaluation method for supplier
- ↑ Fuh-Hwa Franklin Liu, Hui Lin Hai, The voting analytic hierarchy process method for selecting supplier, International Journal of Production Economics, Volume 97, Issue 3, 2005, Pages 308-317 https://www.sciencedirect.com/science/article/pii/S0925527304003263
- ↑ 6.0 6.1 Saaty, Int. J. Services Sciences, Vol. 1, No. 1, 2008 https://www.rafikulislam.com/uploads/resourses/197245512559a37aadea6d.pdf
- ↑ Asadabadi et al., Are MCDM methods useful? A critical review of Analytic Hierarchy Process (AHP) and AnalyticNetwork Process (ANP), Cogent Engineering(2019), 6: 1623153 https://www.rafikulislam.com/uploads/resourses/197245512559a37aadea6d.pdf