Critical path vs. critical chain

Developed by Sophia Lykke Andersen

Abstract

This article attempts to clarify the difference between two well-established phenomena in project scheduling, which are often confused: critical path and critical chain.

In project management, keeping track of critical project activities is key to managing a schedule. The critical path and critical chain are relevant to project management as these enables the project manager to properly manage the project schedule via e.g. accurate estimation of the project duration, and identification of task dependencies and resource constraints. .

When activities have to finish before others can start, start before others can finish, or other relationships, paths of activity dependence form. The longest path of activities related to one another from start to finish of a project will be the most critical, as delays within this path will cause the whole project to be delayed. From this phenomenon, the definition of the critical path rises. In real life, the critical path will only be the most critical considering all resources available at all times, people, materials, space, etc. As soon as resources are limited, other activities or paths of activities can become more critical.
Allocating resources, considering additional constraints, and viewing the project schedule from a holistic point of view allows the manager to see a chain of criticalities within the project. The critical chain will be the longest path of activities considering activity independence and resource constraints as well.
The article will take the reader through a historical perspective, go over the methods of the two phenomena, and provide an example in order to get a more hands-on understanding. In the end, a discussion of the principle differences between the two phenomena will be made, providing the reader with a better understanding of the limitations of each method and when what applies. Furthermore, a glossary explaining the different terms associated with the two phenomena is given.
The article contains the following topics: Glossary, History, Critical path (Method, Example), Critical chain (Method, Example), and Discussion (Differences, Limitations).

Core difference

A critical path identifies the longest path of activities to be finished in order to end the project .
A critical chain identifies the longest path of activities to be finished in order to end the project also considering resource constraints .

History

The critical path method, also known as CPM, was developed by James E. Kelley from Remington Rand and Morgan R. Walker from DuPont at the end of the 1950s, as a tool against ineffective project planning. They figured that costs could be lowered by making sure that the right project activities were carried out at the right time. Around the same time, the American Navy and Booz Allen Hamilton developed a similar method; the Program Evaluation and Review Technique, also known as PERT. Kelley and Walker published their work in 1959, but back in the 1940s, parts of the technique were already used and contributed to the success of the Manhattan project.
In the 1960s, larger companies such as Mauchly Associates and Catalytic Construction started to make use of the critical path method, but it was not until the technical revolution of computers that the method could be used without large costs for companies.
Today... (reference to the programs section)

Glossary

Activity: ...
Network: ---
Forward pass:
Backwind pass:
Early start:
Late start:
Early finish:
Late finish:
Predecessor:
Successor:
Start-Start: ...
Finish-Finish: ...
Start-Finish: ...
Finish-Start: ...
...

The methods

Critical path

- Method
- Example

The following section will take the reader through the method of identifying the critical path, by making use of an example. The method of finding the critical path in a network requires a list of the activities with resp. durations, as well as dependencies. An example of such a list can be found below.

List of activities and their dependencies and durations

Activity	Predecessor	Successor	Duration
A	C	F	2
B	C	H	3
C	---	A, B, D	4
D	C	I, H	2
E	J	---	3
F	A	T, K	2
G	I	M	3
H	B, D	J	4
I	D	G	2
J	K, H	E	2
K	F	J	1
M	T,G	---	3
T	F	M	1

Activities with no predecessors mark the beginning of the project (written as "---" in the table above). The dependencies are defined and mapped out by identifying the predecessor of each activity. From the start node, all the activities with no predecessors are drawn as arrows to each their resp. end node. In this example, the only activity with no predecessor is C. As A, B, and D all have C as their predecessor, arrows representing these activities are drawn from C's end node. Likewise, the rest of the activities are drawn as arrows from the end node of their predecessors. If an activity has more than one predecessor, a dummy predecessor is drawn as a dotted arrow, to indicate the dependency, but not an actual activity. The below image shows the drawn network according to the example:

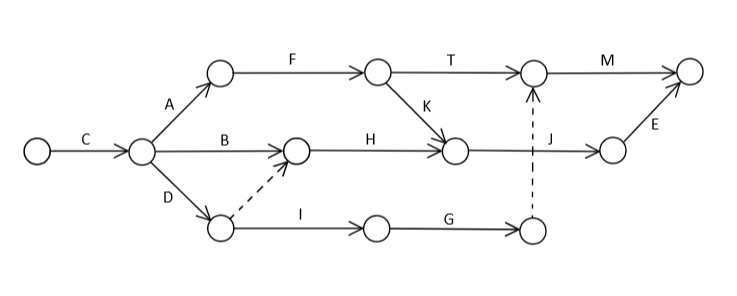
A check can be made by going back through the drawn network, making use of each activity's successors. An activity with no successor should be pointing towards the end node of the whole network, like the activities M and E in the example.
When the network is mapped out the forward pass can be carried out considering the duration of each activity. No activity can start before the day after the last day of its predecessor activity. As C in the example takes 4 days to complete, A, B, and D cannot start before day no. 5. The earliest start of each activity is identified and the duration of the project can be found. Now the backward pass can be performed. This is done by going through the network starting at the finish day and considering the duration of each activity going backward. The latest possible start day for each activity, in order to finish at the end date of the project, is identified. The below image shows the network with added early start, early finish, late start, and late finish:

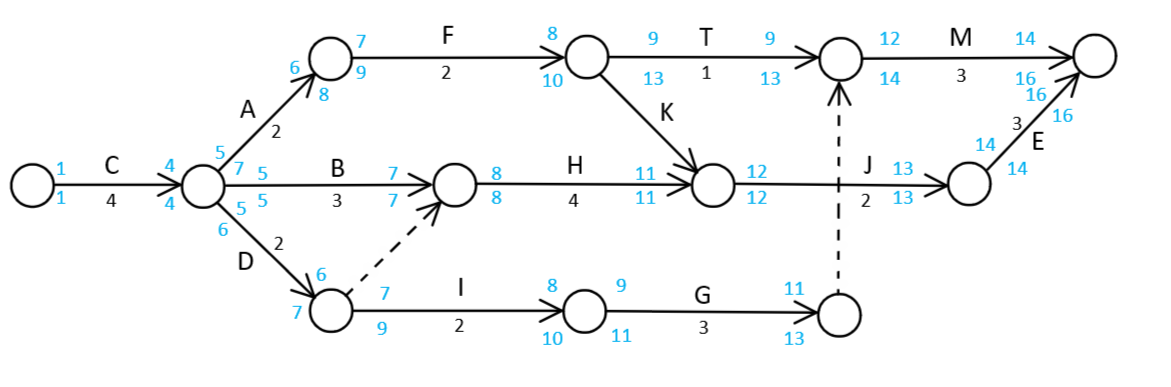
The internal float of an activity, also called...?, is the difference between the early start date and the early finish date of an activity. Activities that can latest start the same day as it can earliest start will have an internal float of 0. Activities with a float of zero will be on the critical path, as delays of these activities will delay the whole project.
<image of network with a critical path marked >

Critical chain

- Method
- Example

A description and then the same example is used again, adding resources and finding the critical chain. <image of network with a critical chain marked >

Programs

A list of the common programs used to calculate the critical path

Limitations

- Differences between the phenomena/methods
- Limitations to each method
- Where is what used and Where to use what ?

Limitations: critically reflect on the tool/concept/theory and its application context. What can it do, what can it not do? Under what circumstances should it be used, and when not? How does it compare to the “status quo” of the standards – is it part of it, or does it extent them? Discuss your article in the context of key readings / resources provided in class. Substantiate your claims with literature