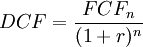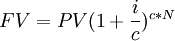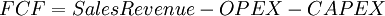Discounted cash flow

Developed by Oliver Skou Schwarz

This page refers to the discounted cash flow (DCF) method regarding projects and investments. It is used to evaluate if a project is worth pursuing based on its future financial merits. Discounted Cash Flow (DCF) is a method used to estimate the value of an investment or a project by projecting its future cash flows and then discounting them back to their present value (PV). The reason for using DCF is that an investment's value is equal to the sum of its expected future cash flows, discounted at an appropriate rate to account for the time value of money and the potential risk involved in the investment. The sum of the discounted cash flow is the Net Present Value (NPV). Since the discounted cash flow is such a big part of the NPV, the two are almost interchangable when it comes to calculations.

Origin

The idea of discounted cash flow has been utilized in one way or another for centuries. However, The modern version trace back to the early 20th century, where it was used in finance and to analyse investments. One of the most influencial modern uses of DCF was in 1930 by American economist Irving Fisher in "The Theory of Interest." Fisher used DCF to calculate the present value of future cash flows, which he coined the "net present value" of an investment. Since then, this method has been widely used in valuation, including in finance, investment, and portfolio management.

Math section

Formula

The discounted cash flow is a way of calculating the present value of a future free cash flow, evaluated at a given discount rate. That means any single given cash flow can be brought back to the value of the present. The formula for the DCF can be seen below.

$DCF = \frac{FCF_n}{(1+r)^n}$

Where

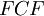$FCF$ is a free cash flow.

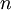$n$ is the year in the forecasted period $N$.

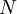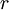$r$ is the discount rate.

As the present value of a single cash flow is not that useful on its own, usually the formula is applied on a number of cash flows, corresponding to each year in a period. When done like this, the formula becomes a series of discounted cash flows added together. An example of this can be seen below.

$DCF = \frac{FCF_1}{(1+r)^1} +\frac{FCF_2}{(1+r)^2} +...\frac{FCF_N}{(1+r)^N}$

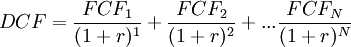
This can be used to assign value to a project or a business by assessing the cash flows it will generate within the forecasted period 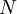$N$. Since the formula operates with increasing years, the further away in the future the cash flow is, the lower the present value of it will be. This is due to the time value of money.

Discount Rate

The discounted cash flow formula is highly dependent on the discount rate 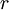$r$. The discount rate is a rate of interest which is applied to the future cash flows of an investment or a business, which determines the final Net Present Value (NPV). There are several ways of determining the appropriate discount rate, but some level of uncertainty will always occur. For many intents and purposes, the discount rate is assumed to a certain value. However, for more precise values, there are ways of estimating it. Some of the most prevalent types of discount rate include :

• Weighted Average Cost of Capital (WACC)
• Hurdle Rate
• Cost of Equity
• Cost of Debt

In this article, the WACC will be discussed in a later section.

Example

A simple example is given below. In this case, the DCF is only calculated for a single cash flow, 1 year from present. In this way, the result will be value of a cash flow a year from now in today's money. In this simple example, the business is a lemonade stand. The lemonade stand has a yearly total cost of 100$ and a yearly total revenue of 200$ in year 1. This will mean that the free cash flow (FCF) for year 1 is:

$FCF_1 = 200$ - 100$ = 100$$

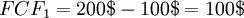
Now, it is assumed that there is a discount rate 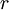$r$ of 6%. With this, the final DCF for year 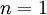$n=1$ can be calculated as:

$DCF_1 = \frac{FCF_1}{(1+r)^n} = \frac{100$}{(1+0.06)^1} = 88.99$$

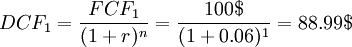
This means that even though the lemonade stand will generate 100$ next year, this is only worth 88.99$ today.

Application

This section highlights the application of DCF as well as important principles that are deeply connected to the method of discounting cash flows.

Time value of money

The time value of money (TVM) is an important concept that states that monetary value changes over time. Practically, this means that any sum of money today is worth more than the exact same amount of money in the future. Herefrom the expression "A dollar today is worth more than a dollar tomorrow." The reason behind this is that money today has the potential to be used to generate more money by investing, whereas money in the future can only be invested in the future, and thus loses its earnings potential. Furthermore, factors like inflation and interest rates contribute to the fact that money can lose its value over time. Therefore, the time value of money is an important principle in projects and when investing in them, as it helps project managers and businesses make better decisions about how to allocate resources smartly. The TVM can be calculated both for present values and future values. The equation for future value (FV) can be seen below:

$FV = PV(1+\frac{i}{c})^{c*N}$

Where

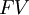$FV$ is the future value

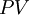$PV$ is the present value

$i$ is the interest rate

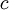$c$ is the compoundings per year

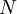$N$ is the number of years

This equation can be used to estimate the value of a sum of money today in the future. It is highly dependent on the number of compounding periods per year.

Free Cash Flow

The free cash flow (FCF) is the cash flow that is available to equity holders and debt holders after a business pays for the costs of continued operations, like operating expences and capital expenditures. Generally, the more free cash flow a business or a project has, the more attractive it will be for investors, as it will be able to invest in new opportunities. There are multiple ways of calculating the free cash flows depending on the level of precision and complexity. A simple model for calculating this can be seen below.

$F C F = Sales Revenue - OPEX - CAPEX$

The sales revenue is the money going into the project or the business, hence the positive sign.

The Operational Expenditure (OPEX) refers to the recurring short-term cost of maintaining the operations of a project or a company on a daily basis. This could be the cost of necessities such as rent, electricity, staff salaries, and other costs associated with delivering a project's desired outcome on a day-to-day scale.

CAPEX is the Capital Expenditures, which refers to the amnount fo money a company or a project need to invest in acquiring its long-term assets needed to start operations. This can include assets such as property, equipment, or technology. Capital Expenditures are generally more expensive and long-term than other expenses, such as the operational expenditure, and are considered investments in the company's future.

The Free Cash Flow is in this instance calculated for a single year. However, doing it for multiple years is necessary. Generally speaking, the FCF needs to be projected until it reaches a steady state (typically 5 to 10 years).

Example

As the previous example mentioned, the free cash flow needed to be used in the DCF formula. However, the equation for finding the FCF for a lemonade stand was somewhat simplified. As can be seen from the equation for FCF, the free cash flow equals the total sales revenue (or other generated income) minus the total costs. However, this time the costs are divided into two categories. Operational costs and capital costs. Using the same numbers as the previous example, we have that the total sales revenue of the lemonade stand is 200$. The operational expenses are costs such as ingredients to make the lemonade (sugar, lemons, ice etc.). These are the things that are needed on a daily basis. On the other hand the capital expenses might be things like the actual stand and the sign - things that are invested in once in the beginning of the "venture."

We than have that:

$SalesRevenue = 200$$

$OPEX = 60$$

$CAPEX = 40$$

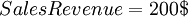
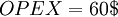
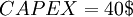
Putting it all into the formula, we get the same free cash flow for the first year as in the DCF example:

$FCF = SalesRevenue - OPEX - CAPEX = 200$ - 60$ - 40$ = 100$$

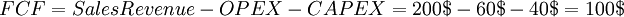
As this is just the free cash flow for one year, when calculating the NPV, cash flows for multiple years are required.

Net Present Value (NPV)

Net Present Value (NPV) is a financial metric used to estimate the current value of an investment based on its expected cash flows and the time value of money. It measures the difference between the present value of cash inflows and the present value of cash outflows over a specified period of time.

[INSERT FORMULAS HERE]

To calculate the NPV, the expected cash flows of the investment are discounted back to their present value using a discount rate that reflects the time value of money and the risk of the investment. The discounted cash inflows are then subtracted from the discounted cash outflows to arrive at the net present value of the investment.

If the net present value is positive, it means that the investment is expected to generate more cash inflows than outflows and is considered profitable. Conversely, if the net present value is negative, it means that the investment is expected to generate less cash inflows than outflows and is considered unprofitable.

NPV is a commonly used financial metric in capital budgeting, where it is used to evaluate the financial viability of long-term investment projects such as the construction of a new plant or the development of a new product. It helps decision-makers determine whether an investment will create value for the company and whether it is worth pursuing.

SORUCE

Working Average Cost of Capital (WACC)

The Weighted Average Cost of Capital (WACC) is a financial method used to measure the cost of capital. It uses the cost of both debt and equity financing, as well as the proportion of each in the company's capital structure.

[INSERT FORMULAS HERE]

The WACC formula calculates the average cost of capital by multiplying the cost of each capital component (debt and equity) by its weight in the company's capital structure.

The WACC is an important financial metric as it is used to evaluate the financial feasibility of potential investment opportunities. The WACC is typically used as the discount rate in discounted cash flow (DCF) analysis to determine the present value of future cash flows.

A higher WACC indicates a higher cost of capital and a greater risk associated with an investment opportunity. On the contrary, a lower WACC indicates a lower cost of capital and a lower risk associated with an investment opportunity.

SOURCE

Terminal Value

The Terminal Value (TV) is the value of the firm or the project after the forecasted period. It is another important method that is used when trying to calculate the present value of a firm or an investment. As the discounted cash flow is done over a certain forecasted period, ususally a couple of years, the NPV of the company will be based only on the present values of the cash flows within this time period. However, in reality, companies keep going after the end of the forecasted period. This means that a company or the product of a completed project will still continue to generate cash flows after the forecasted period. The Terminal Value is then a technique used to capture all the cash flows that comes after the forecasted period and to infinity. This is done by assuming a steady state of growth for the business for eternity. This is called the Perpetuity Growth method, for which the formula can be seen below.

$TV = \frac{FCF_N*(1-g)}{WACC-g}$

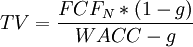
where

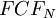$FCF_N$ is the final free cash flow in year N

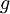$g$ is the growth rate

The value that is calculated from this can be added onto the net present value to get a more realistic estimation. However, this method is highly dependant on unknown factors, meaning a lot of assumption will have to be made. This includes the growth rate and the calculated WACC.

Investments in Projects (references to NPV as well)

A section with specific reference to projects and investments in these, possible examples from real life application of it and other methods that are similar or (better/worse) in certain cases.

• Projects
• Real example
• How and when similar models were used

Limitations

A section describing the cons of the methods, with a critical perspective on possible assumptions of the model.

SOURCE

How to calculate

A brief section with concrete advice on how it should be applied for the reader - this may need to not be the last section.

• example of how to use the formula, with numbers
• Assumptions

References

Possible Sources:

https://www.pmi.org/learning/library/project-investment-9384

(PROJECT INVESTMENT https://esfccompany.com/en/articles/economics-and-finance/investment-project-management/)