Parkinson's Law

C. Northcote Parkinson, a British naval historian best known for his best-seller book 'Parkinson's Law: The Pursuit of Progress' (1957), once expressed in an essay to The Economist, that 'Work Expands To Fit The Time Available For Its Completion', in what is now known as Parkinson’s Law . One consequence of this is that the number of administrators within a public organization tends to increase regardless of the amount of work done externally by set organization [2][3]. For instance, an elderly lady of leisure can spend a whole day merely composing and sending a postcard to a niece. An hour spent finding the postcard, another looking for spectacles, an hour and a half in composition, and another thirty minutes in deciding whether to wear a coat when heading to the postbox .

Similarly, if a task must be done in a year, it will be done in a year. If something must be done in a week; it will be done in a week. The completion of tasks is planned, as the deadline approaches, based on various choices and tradeoffs necessary to complete a task by set deadline [4]. However, using Parkinson’s Law to set unreasonable goals/deadlines is not at all its purpose. The goal of this article is to illuminate when the use of the Law is appropriate, and in which context it provides the greatest benefits, while elucidating its shortcomings/limitations.

History and Purpose

Parkinson’s Law was first published in an article in The Economist in November 1955, reflecting on how work could be viewed as elastic in its demands on time [1]. The Law not only applies to individuals, but also teams, organizations, armed forces, universities, corporations etc. [5] Several automatic and purposeful factors are at play. There is a defensive desire to appear busy when there is no work to be done. There is a desire to be prolific and to multiply employees. Furthermore, there is a general propensity to just procrastinate. The Law states in general why the useful work done depends vaguely on the number of employees, overtime policies, vacation schedules, or retirement practices. Thus, the compound growth rate of a bureaucracy or its feverish activity are not indices of its effectiveness [5]. The Law’s validity is heavily reliant on statistical proofs, of which two motive forces can be represented by two nearly axiomatic statements: 1) “An official wants to multiply subordinates, not rivals”, and 2) “Officials make work for each other” [6]. These forces/factors are further explored in sub laws named: 1) The Law of Multiplication of Subordinates, and 2) The Law of Multiplication of Work.

The Law of Multiplication of Subordinates

To understand the validity of the first factor, a thought experiment was postulated in the article for Parkinson’s Law in The Economist, regarding a civil servant designated as A, who finds themselves overworked. It is immaterial whether this stress is legitimate or imaginary. However, it should be noted that A’s sensation may be the result of the decreasing energy that is normally accompanied with age. From the viewpoint of A, there are a total of three possible remedies, proposed by C. Northcote Parkinson [1]:

1. They may resign.
2. They may ask to halve the work with a colleague called B.
3. They may demand the assistance of two subordinates to be called C and D.

In the 1955 article, it is reasoned that throughout civil service history, there has been no instance in which A has chosen any but the third alternative. Resignation would deny A of their pension rights, and by appointing B, A would merely bring a rival for promotion to a higher position, should a vacancy occur. Therefore, A would rater have subordinates C and D, below them [1]. Another point to realize in law of subordinates is that C and D are inseparable, since appointment of i.e., C alone would have been impossible. This is because C would divide the work with A and therefore assume nearly the equal status if B were appointed instead; further emphasized if C is A’s only apparent successor.

The Law of Multiplication of Work

In this thought experiment, where seven officials are now doing what one did before, is where the second factor now plays a role. The seven officials make much work for each other, making them all fully occupied while A is working harder than ever. One incoming document may very well come before each of them in turn. In this example, E decides that the contents of the document fall into the province of F, who then places a draft reply to C, who amends it exceedingly before consulting D, who asks G to handle it. However, G is absent on leave in this point in time, and therefore forwards it to H, who drafts a minute, signed by D, and returned to C, who once more revises his draft accordingly and lays this version before A [1].

A now has a choice to make regarding signing the thing unread, therefore also deciding whether C or D should succeed to his own office. Considering F’s special increment of salary for the period of the conference, and E’s application for transfer to the Ministry of Pensions. This along with other countless considerations may color A’s intentions, thus tempting A to sign C’s draft and have it done with. However, being conscientious, A decides to go through the draft with care, deleting unnecessary paragraphs and restores the document to the form preferred by F. A then produces the same reply they would have written if C through H had never existed [1]. The results of this thought experiment have thus showed that far more people have taken far longer to produce the same result. No official has stayed idle. All parties have done their best.

Parkinson's Law in Mathematical Form

C. Northcote Parkinson presented, in The Economist, statistical data from British Navy Estimates. These Admiralty statistics were recorded for 1914 and 1928, in which an increase in Admiralty officials from 2,000 as of 1914 to 3,569 in 1928, had been recorded; and that this growth was unrelated to any possible increase in their work. The goal for such an in-depth analysis of the growth of workers in administrative positions, was to find a correlation between a given official’s appointment and the later appointment of his two or more assistants. When focused on pure staff accumulation, all findings so far pointed to an average increase of about 5,75 percent per year. Subsequently, it now possible to state Parkinson’s Law in mathematical form, thus:

In any public administrative department not actually at war, a staff increase may be expected to follow this formula [7]:

$x=\frac{2k^m+p}{n}$

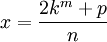
In which:

k – number of staff seeking promotion through the appointment of subordinates.

p – difference between the ages of appointment and retirement

m – number of man-hours devoted to answering minutes within the department.

n – number of effective units being administered.

x – number of new staff required each year.

It should be noted that to find the percentage increase, one must multiply x by 100 and divide by the total from the previous year (y), thus:

$100\cdot \frac{2k^m+p}{yn}%$

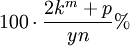
It is however stated that the discovery of this formula has no emotive value. That Parkinson’s Law is a purely scientific discovery, inapplicable except in theory to the politics of the day.