Net Present Value (NPV)
Written by Deepthi Tharaka Parana Liyanage Don- s203116
Contents |
Abstract
Financial appraisal is a method used to evaluate the viability of a proposed project or portfolio of investment projects by evaluating the benefits and costs that result from its execution. Investment decisions of the management are critical to a company since it decides the future of the company. This article discusses the Net Present Value (NPV) method which is widely used in financial appraisal. NPV is a dynamic financial appraisal method that considers the time value of money by applying discounting and compounding of all payment series during the investment period[1]. In simple terms, the net present value is the difference between an investment object’s incoming and outgoing payments at present time. NPV is determined by calculating the outgoing cashflows (costs) and incoming cash flows (benefits) for each period of an investment. After the cash flow for each period is calculated, the present value (PV) of each one is achieved by discounting its future value using the suitable discount rate. Net Present Value is the cumulative value of all the discounted future cash flows[2].
Firstly, this article discusses the idea behind the Net Present Value method and its underlying assumptions. Then this introduces the NPV calculation method[1] and describes the importance of the variables in the formula such as discount rate. Also, it highlights the decision criteria behind NPV and explains it with a real-life application. Finally, it critically reflects on the limitations of this method and briefly introduces the other alternative financial apprisal methods such as Internal Rate of Return (IRR), payback method, and Return on Investment (ROI).
Big Idea
Project business case development is a critical point in a project where it uses to obtain the approval for investment in the project by presenting the benefits, cost, and risk associated with alternative options and the method of selecting the preferred solution. In a business case, financial appraisal plays a key role to answer the fundamental economic questions of whether an investment should be made and which project should be chosen among a selection of different alternatives. Because the task of financial appraisal is to predict the financial effects of planned investment and to present the data in such a way that a reasoned investment decision can be reached[1]. The net present value (NPV) method is the most frequently used approach in the financial appraisal of a project.
What is NPV?
Net Present Value (NPV) is defined as the present value of the future net cash flows from an investment project. In simple terms, the net present value (NPV) is the difference between the present value of all future incoming cash flows and the present value of all future outgoing cash flows. NPV is a widely used method in financial appraisal that considers the time value of money by applying discounting or compounding of all payment series during the investment period[3].
Time value of money
Time value of money means that a sum of money is worth more now than the same sum of money in the future. That is because you can use it to make more money by running a business, buying something now and selling it later for more, or simply putting it in the bank and earning interest. Money can grow only through investing and investment delay is an opportunity cost. [invest-change]Future money is also less valuable because inflation erodes its buying power. NPV assesses the profitability of a given project on the basis that a dollar in the future is not worth the same as a dollar today. The time value of money is recognized in NPV by applying discounting to all payment series during the investment period[3].
Formula
The following formula use these common variables:
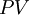 – Present Value
– Present Value
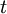 - time of the cashflow
- time of the cashflow
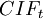 - Cash inflows in period t
- Cash inflows in period t
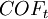 – Cash outflows in period t
– Cash outflows in period t
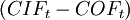 – Net cashflow in period t
– Net cashflow in period t
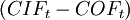 – Net cashflow in period t
– Net cashflow in period t
 – The discount rate
– The discount rate
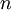 – Total number of periods
– Total number of periods
In order to consider the time value of money the net present value method considers the value of an investment at the present time by converting all information of the future into a key figure at the time today. This projection of the value that a future cash flow has in the present is called "present value" (PV).
To get the Present value (PV) of future cash flows, they are discounted using:
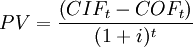
Net present value combines these projections of incoming cash flows (revenues/benefits) and outgoing cash flows (costs) to assess the overall value of a project from the present view.
The net present value is calculated as the present value of all future incoming cash flows, minus the present value of all future outgoing cash flows.
The net present value is given by:
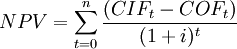
This specification allows the possible incorporation of payments from earlier periods and time periods t < 0 can also be considered.
The discount factor 1/(1 + i)t is automatically converted into a compounding factor and the final value of all cash flows which occur
before time 0 is correctly assessed in t = 0[1].[Change this]
For normal investments, which are characterized by a cash outflow in time t0 followed only by net cash flows 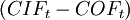 > 0 it holds that:
> 0 it holds that:
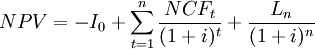
As a summary, the following steps are recommended for the calculation of the Net present value[1]:
- Determination of the initial outflow for the investment.
- Estimate the expected net cash flows from the investment for each period of the planning horizon.
- Determination of the discount uniform rate (it is assumed that the discount rate remains unchanged over the life of the investment), in other words, the rate of return required by the investor.
- Discounting of the expected net cash flows with the discount rate to the time period when the investment is made (determination of the present value).
- Subtraction of the initial outflow for the investment from the present value. This yields the net present value (NPV).
Other NPV Formula
NPV with an annuity
If the net cash inflows are uniform and equidistant and occur at the end of each period, the series of net cash flows can be interpreted as an annuity. Using the formula for the present value of an ordinary annuity, it follows that:
![N P V=-I_{0}+N C F \cdot\left[\frac{(1+i)^{n}-1}{i \cdot(1+i)^{n}}\right]+\frac{L_{n}}{(1+i)^{n}}](/images/math/f/b/b/fbb9818d6744581d2a9ff5023d8e9138.png)
Discount Factor
This section describes how to select the discount factor and its importance.
Time period
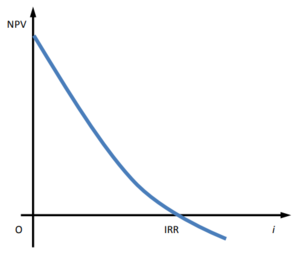
Decision rule
This gives the decision criteria of NPV.
Applications
Application of NPV in real example
Limitations
Introduce the limitations of NPV
Alternative financial appraisal methods
This section gives a brief idea about other methods
- IRR
- payback
- ROI
Annotated Bibliography
Reference Example: The book-1.[1] The book-2.[2] The book-3.[3] The book-4.[4] The book-5.[5]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Häcker J. and Ernst D., Ch. 8 - Investment Appraisal. In: Financial Modeling. Global Financial Markets., (Palgrave Macmillan, London, 2017), pp. 343-384, https://doi.org/10.1057/978-1-137-42658-1_8
- ↑ 2.0 2.1 Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models., (Elsevier, 2018), pp. 85-114, https://doi.org/10.1016/C2016-0-03558-1
- ↑ 3.0 3.1 3.2 Konstantin P. and Konstantin M., Ch. 4 - Investment Appraisal Methods. In: Power and Energy Systems Engineering Economics., (Springer, Cham, 2018), pp. 39-64, https://doi.org/10.1007/978-3-319-72383-9_4
- ↑ Poggensee K. and Poggensee J., Ch. 3 - Dynamic Investment Calculation Methods. In: Investment Valuation and Appraisal., (Springer, Cham, 2021), pp. 85-140, https://doi.org/10.1007/978-3-030-62440-8
- ↑ Ing E. and Lester A., Ch. 6 - Investment Appraisal. In: Project Management, Planning and Control. 7th Edition., (Elsevier, 2017), pp. 29-36, https://doi.org/10.1016/B978-0-08-102020-3.00006-1