Internal rate of return (IRR)

[Lorenzo Incarnato s220426]

- references - pictures

Abstract

The Internal Rate of Return (IRR) is a powerful discounted cash flow method used in capital budgeting and corporate finance to estimate and evaluate the profitability of potential investments. Keeping in mind the formula for the Net present value (NPV), the IRR is defined as the discount rate that makes the present value of the costs (negative cash flows) of an investment equal to the present value of the benefits (positive cash flows). In other words, the IRR is the discount rate that gives a net present value of zero when applied to the expected cash flow of a project. This rate of return is called internal because the formula predicts a rate that depends only on the project, more precisely on the project's cash flows, and does not depend on external factors such as market interest rates or inflation. One of the main advantages in using the internal rate of return to evaluate project investments, compared to other methods such as the Payback period or the Benefit-cost ratio, is that IRR reflects the time value of money. In general, due to the relationship between NPV and IRR, the higher the Internal Rate of Return of a project, the more desirable the investment to be made. This article shows also the limitations of the internal rate of return; however, when the IRR is unique, it provides relevant information about the return on investment and is also used as a measure of investment efficiency. In fact, according to academic research, three-quarters of Chief Financial Officers use the IRR method to evaluate capital projects.

Time value of money

Would you rather have $ 100,000 now or a year from now?

This paragraph explains the reasons why a certain amount of money available today is worth more than having the same amount in the future. In short, it tries to deepen the concept of time value of money (TVM).

A certain amount of money available today (present value) does not correspond to the same amount in the future (future value) because, in finance, the present value could be invested and grow based on the interest rate, generating more money in the future. This relation between the same amount of money available on two different dates, today and in the future, is called the Time Value of Money. It is, therefore, necessary to briefly underline three fundamental terms about investments:

• the Present value (PV): the sum of money available today that can be invested [$];
• the Interest rate (r): the amount of interest due per period, as a proportion of the amount deposited/borrowed [%]
• Future value (FV): is the value of a current asset (present value) at a future date based on an assumed rate of growth (interest rate) [$].

So to calculate how much money will be $ 100,000 in the future, you need to know the interest rate (or the opportunity cost if we decide not to invest). For this example, assume an interest rate r = 3%. Hence, considering the generic formula for the future value:

$FV = PV * (1 + r)^n$

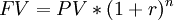
So, it is easy to understand that having 100 000$ now corresponds to have 103 000$ in the future and, hence, if we agreed to receive $ 100,000 in a year instead of now, considering a 3% opportunity cost (as in the example), we would have $ 3,000 less. the answer to the initial question (Is $ 100,000 the same value today in a year?) is: no. More precisely, applying the formula of the future value (FV), 100 000$ today equals to:

$FV = PV * (1 + r) = 100,000$ * (1 + 0.03) = 103,000$$

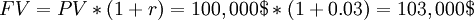
Hence,. Now, considering the generic formula for the future value (with n years):

Hence, a certain sum available in the present could be invested and grow according to the interest rate. The amount of money cumulated in the meantime is the Time Value of Money, mathematically TVM = FV - PV.