Internal rate of return (IRR)

[Lorenzo Incarnato s220426]

- references - pictures

Abstract

The Internal Rate of Return (IRR) is a powerful discounted cash flow method used in capital budgeting and corporate finance to estimate and evaluate the profitability of potential investments. Keeping in mind the formula for the Net present value (NPV), the IRR is defined as the discount rate that makes the present value of the costs (negative cash flows) of an investment equal to the present value of the benefits (positive cash flows). In other words, the IRR is the discount rate that gives a net present value of zero when applied to the expected cash flow of a project. This rate of return is called internal because the formula predicts a rate that depends only on the project, more precisely on the project's cash flows, and does not depend on external factors such as market interest rates or inflation. One of the main advantages in using the internal rate of return to evaluate project investments, compared to other methods such as the Payback period or the Benefit-cost ratio, is that IRR reflects the time value of money. In general, due to the relationship between NPV and IRR, the higher the Internal Rate of Return of a project, the more desirable the investment to be made. This article shows also the limitations of the internal rate of return; however, when the IRR is unique, it provides relevant information about the return on investment and is also used as a measure of investment efficiency. In fact, according to academic research, three-quarters of Chief Financial Officers use the IRR method to evaluate capital projects.

Time value of money

A crucial consideration regarding discounted cash flow methods is the Time Value of Money (TVM). This paragraph explains why money tomorrow is not as valuable as money today, calculating their values through an example.

How can we compare money available in the present and in the future?

In finance, the time has a monetary value. A certain amount of money available today or in the future has a different value because today you have the opportunity to invest the money and thus grow, according to the time horizon and the interest rate. Another reason for the time value of money is that the purchasing power of money which changes over time due to inflation or Wikipedia: deflatiodeflation. It can be concluded that, in order to compare money available in two different moments, it is needed to consider the time value of money, which enable us to discount' money available in the future and consider them in the present or vice versa; then we can compare the two amounts. It is, therefore, necessary to briefly underline three fundamental terms about investments to clearly understand the time value of money:

• The Present value (PV): the sum of money available today that can be invested [$];
• The Interest rate (r): the amount of interest due per period, as a proportion of the amount deposited or borrowed [%]
• The Future value (FV): is the value of a current asset (present value) at a future date based on an assumed rate of growth (interest rate) [$].

Present to Future	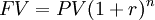$FV = PV (1 + r)^n$
Future to Present	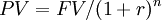$PV = FV / (1 + r)^n$

Would you rather have $ 100,000 today or the same amount in 1 year from now?'

Let's consider an example: how much money we should invest now if we want $ 100 000 in two years from now considering an annual interest rate of 7%? Applying the present value formula, we should invest:

$PV = FV / (1 + r)^n = $ 100,000 / (1 + 0.07)^2 = $ 87,3743$

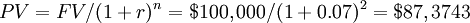
3. If your answer is to have the money today, what will be the X amount of money in 1 year to have the indifference of choice?

, which means that this method regards the present value of future cash flows generated by investments. This means that receiving a certain amount of money today does not correspond to receiving the same amount of money in the future. In finance, the time has a monetary value. In fact, the present value could be invested and grow based on the interest rate, generating more money in the future. This relation between money and time is called the Time Value of Money. It is, therefore, necessary to briefly underline three fundamental terms about investments:

• The Present value (PV): the sum of money available today that can be invested [$];
• The Interest rate (r): the amount of interest due per period, as a proportion of the amount deposited or borrowed [%]
• The Future value (FV): is the value of a current asset (present value) at a future date based on an assumed rate of growth (interest rate) [$].

Is it financially better getting $ 100 000 now or in a year from now? Is there any difference? To calculate how much money will be $ 100,000 in a year from now, supposing an interest rate (or opportunity cost if we decide not to invest) r = 3%, we can apply the generic formula for the future value:

$FV = PV * (1 + r)^n = 100,000 $ * (1 + 0.03)^1 = 103,000 $$

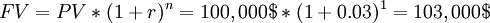
So, having 100 000$ now corresponds to having 103 000$ in the future. If we agreed to receive $ 100,000 in a year instead of now, considering a 3% opportunity cost, we would have $ 3,000 less. This difference is the Time Value of Money and it is strighlty related to the concept of interest rate .

[continue...]