Internal rate of return (IRR)

[Lorenzo Incarnato s220426]

- references - pictures

Abstract

The Internal Rate of Return (IRR) is a powerful discounted cash flow method used in capital budgeting and corporate finance to estimate and evaluate the profitability of potential investments. Keeping in mind the formula for the Net present value (NPV), the IRR is defined as the discount rate that makes the present value of the costs (negative cash flows) of an investment equal to the present value of the benefits (positive cash flows). In other words, the IRR is the discount rate that gives a net present value of zero when applied to the expected cash flow of a project. This rate of return is called internal because the formula predicts a rate that depends only on the project, more precisely on the project's cash flows, and does not depend on external factors such as market interest rates or inflation. One of the main advantages in using the internal rate of return to evaluate project investments, compared to other methods such as the Payback period or the Benefit-cost ratio, is that IRR considers the time value of money. In general, due to the relationship between NPV and IRR, the higher the Internal Rate of Return of a project, the more desirable the investment to be made. This article shows also the limitations of the internal rate of return; however, when the IRR is unique, it provides relevant information about the return on investment and is also used as a measure of investment efficiency. In fact, according to academic research, three-quarters of Chief Financial Officers use the IRR method to evaluate capital projects.

Time value of money

To compare the cash flows available at different times, we must therefore include the time value of money, which states that there is a difference between the future value of the payment and the present value of the payment itself. So, to know the discounted cash flows of the project, therefore, it is necessary to discount the future cash flows through the discounting process. The reverse process, to be able to compare cash flows in the future, is called compounding .

Present to Future (compounding)	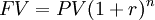$FV = PV (1 + r)^n$
Future to Present (discounting)	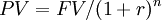$PV = FV / (1 + r)^n$

The monetary value of project investment is the value of the project's future cash flows (or net benefits) less the required investments (or initial costs). A key consideration regarding discounted cash flow methods is the Time Value of Money (TVM). In finance, an amount of money available today or in the future has a different value because we have to consider that also time has a monetary value. In other words, $ 100 today is not $ 100 tomorrow. The reason is that today you have the opportunity to invest money and thus grow, according to the time horizon and the interest rate. Another reason for the time value of money is the purchasing power of money which changes over time due to inflation or deflation. Hence, the time has a monetary value and we have to consider it if we want to compare money available in different moments . It is, therefore, necessary to briefly underline three fundamental terms about investments to clearly understand the time value of money:

• The Present value PV: the sum of money available today that can be invested [$];
• The Interest rate (or opportunity cost if we decide not to invest) r: the amount of interest due per period, as a proportion of the amount deposited or borrowed [%]
• The Future value FV: is the value of a current asset (present value) at a future date based on an assumed rate of growth (interest rate) [$].

Example 1

Would you rather have $ 100,000 today or the same amount in 1 year from now?

To calculate how much money will be $ 100,000 in a year from now, supposing an interest rate r = 3%, we can apply the formula for the future value:

$FV = PV * (1 + r)^n = $ 100,000 * (1 + 0.03)^1 = $ 103,000$

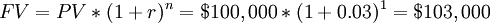
So having $ 100,000 now is equivalent to having $ 103,000 in the future considering an interest rate of 3%. If we agreed to receive $ 100,000 in one year instead of now, we would be $ 3,000 less. As shown, the present value and the future value differ by a factor of 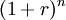$(1+r)^n$; this difference represents the time value of money. It can be concluded that to compare the money available in two different moments it is necessary to consider the time value of money, which allows us to discount money available in the future and consider it in the present or vice versa; only then can we compare the two amounts.

Example 2

Considering an interest rate of 9%, is it better to receive $ 150,000 today or $ 180,000 in three years? What amount of money do you have indifference of choice?

If we invest the present value at an interest rate of 9%, in three years we will have a future value of:

$FV = PV * (1 + r)^n = $ 150,000 * (1 + 0.09)^3 = $ 194,254$

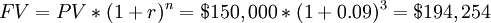
It is better to have $ 150,000 today because by investing it we will have $ 194,254 over three years, which is $ 14,254 more than $ 180,000. To be indifferent, therefore, the amount of money available in three years would have to be $ 194,254.

Example 3

After an initial investment of $ 100,000 for machinery, we expect future cash flows of $ 40 000 annually for the next 4 years, thinking to gain $ 60 000 (-100 000 + 40 000*3) at the end of the period. Is it true?

In finance, to calculate the profitability of a project considering future cash flows, it is needed to consider an alternative investment with almost the same risk to know the interest rate of the other investment. Considering an interest rate r = 7%, we can now calculate the time value of money because we have the interest rate. So,

	cash flow (0)	cash flow (1)	cash flow (2)	cash flow (3)	cash flow (4)
Today	- 100,000
1st year		+ 40,000
2nd year			+ 40,000
3rd year				+ 40,000
4th year					+ 40,000

Discounting all the cash flows with the PV formula:

$PV = FV / ( 1 + r ) ^n$

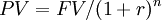
We obtain:

	cash flow (0)	cash flow (1)	cash flow (2)	cash flow (3)	cash flow (4)
Today	- 100,000
1st year	+ $ 37,383	+ 40,000
2nd year	+ $ 34,938		+ 40,000
3rd year	+ $ 32,652			+ 40,000
4th year	+ $ 30,515				+ 40,000
Total cash flow (0)	= $ 35,488

So, the investment is profitable because the total cash flow (0), or Net Present Value, is greater than zero ( $ 35,488). Furthermore, it is lower than $ 60,000 because of the time value of money. From this example, it can be seen two things:

• The Net Present Value is the present cash flow of the project and it is obtained by discounting the cash flows;
• The difference in value between future and present cash flows (time value of money) is inversely proportional to time and the interest rate. This means that the more a cash flow is in the future, the more its value will decrease if it is to be carried over into the present.

IRR: definition and formula

A good understanding of the methodological basis of Net Present Value is required to truly comprehend the essence of the internal rate of return method, as it is closely related to NPV and allows management to add valuable information on decision criteria rather than just look at NPV.

Net Present Value

Net Present Value is a discounted cash flow method used to analyze the profitability of a project and is the difference between the present value of cash inflows and the present value of cash outflows over a period of time. To calculate the NPV of a project with future cash flows, it is necessary to discount them considering the time value of money. The NPV is the sum of these discounted cash flows and reflects the profitability of the project . Mathematically:

$N P V =\sum_{n=0}^{N} \frac{\left(C F_{n}\right)}{(1+ r)^{n}}$

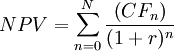
• n: years from 0 to N
• N: time horizon
• CF (n): cash flow relative to n-year
• r: discount rate

The NPV of an investment project reflects in monetary terms the project profitability. In fact, analyzing the formula for NPV it can be concluded that, according to the discount rate (r) considered in the formula:

• if NPV > 0: the discounted inflows are higher than the discounted outflows, hence the investment project will generate profit;
• if NPV < 0: the discounted inflows are lower than the discounted outflows, hence the investment project will generate loss;
• if NPV = 0: the discounted inflows are equal to the discounted outflows, hence the investment project will not generate profit or loss.

Example: A company wants to buy 10 new lathes for $ 50,000 each, considering an annual inflow of $ 10,000 for the first 3 years, $ 15,000 for the 4th and 5th years. How much profit (or loss) can this project generate? Consider three different discount rates: r1 = 11%, r2 = 6%, r3 = 5%. Using the formula for NPV:

$N P V (11%) =\sum_{n=0}^{5} \frac{\left(C F_{n}\right)}{(1+ 0.11)^{n}} = - $ 6780.12$

$N P V (6%) =\sum_{n=0}^{5} \frac{\left(C F_{n}\right)}{(1+ 0.06)^{n}} = - $ 179.60$

$N P V (5%) =\sum_{n=0}^{5} \frac{\left(C F_{n}\right)}{(1+ 0.05)^{n}} = $ 1,325.91$

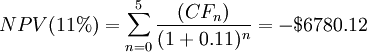
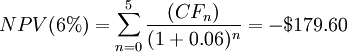
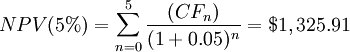
discount rate	NPV
11%	- $ 6780.12
6%	- $ 179.60
5%	$ 1,325.91

it is useful to observe that as the discount rate increases, the NPV decreases, and vice versa. Shortly, they are inversely proportional as shown by graph 1

[continue....]

Decision criteria

[continue...]

IRR > r IRR = r IRR < r

IRR in practice

[continue...]

Internal Rate of Return (IRR) vs Return on Investment (ROI) vs Net Present Value (NPV)

[continue...]

Limitations

Multiple IRRs [continue...]