MCDM-APH method in decision making

The MCDM-APH (Multi-Criteria Decision Making - Analytic Hierarchy Process) is a tool that makes complex decisions. MCDM is a systematic approach that evaluate conflicting criterias in decision making, one of these approaches is APH which uses a mathematic method to derive a relative importance of criteria in a decision problem.

The method was developed in the 1970s by Thomas Saaty , AHP is a mathematical method that is used to derive the relative importance of criteria in a decision problem. The idea behind the method is that a decision problem can be represented as a hierarchical structure, with the most important criteria at the top followed by the lesser important criteria at the bottom.

Decision-making is at the core of project management and yet it can be a daunting task, especially when the projects are complex and multi-facted projects. The pressure of making decisions in a timely and informed manner can be compounded when the criteria for success is not defined clearly, At time like this it not unusual that project managers may feel overwhelmed and unable to determine the most important factors to consider. This is where the APH-decision-making method provides a systematic approach to this challenge. This approach is addressing the complexity of decision making by Segmenting the process into manageable chunks. By following these steps the project manager can get a obtain a holistic view of the project's key performance indicators and success factors.

Project selection

A project manager in the current day is faced with a dynamic environment, where making the right choices based on fitting objective is a crucial factor for weather a organization is profitable or not. Simply completing a project and hope for the best outcome is no longer enough, as the projects are more complex with more risks and dynamic challenges this means that there is a higher demand for a strategic approach.

In order to accomplish this, organizations are using more resources in portfolio management which helps them structurize the projects so they are in alignment with the organizations strategic goals. One of the main part of portfolio management is cost-benefit, where projects with high benefits is given higher priority. The analysis takes into account the benefits of completing a project as well as the cost, as projects become more complex the cost-benefit analysis becomes as complex and hectic.

The analytic hierarchy process

Assuming that we have multiple criterias and alternatives, the weight of the criterias is first weighted using pairwise comparison, using saatys scale:

The foundation scale of absolute numbers
Intensity of importance	Definition	Explanation
1	Equal importance	Two activities contribute equally to the objective
2	Weak or slightly
3	Moderate importance	Experience and judgment slightly favor one activity over another
4	Moderate plus
5	Strong importance	Experience and judgment strongly favor one activity over another
6	Strong plus
7	Very strong	An activity is favored very strongly over another, its dominance demonstrated in practice
8	Very, very strong
9	Extreme importance	The evidence favoring one activity over another is of the highest possible order of affirmation
Table 1: Saatys scale

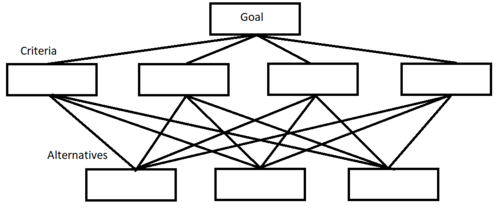
The APH method makes use of the hiracy approach, where the objective is at the top and criteria is below it and the alternatives are at the bottom.

Example for AHP

NOTE TO ME: NEED INTRO

1. Identify the objectives
2. Assign weights to the criteria by performing pairwise comparisons
3. Evaluate the performance of each alternative with respect to each criterion
4. Preform Consistancy test
5. Calculate the global priority of each criteria and ranking

Idenrify the objective

A company is in the process of implementing a PMO system and is considering 3 providors. The company have come up with three specific criteria, which are considered highly important when determining which product they should buy. These criteria are cost, technical support, and flexibility.

Assign weights to the criteria by performing pairwise comparisons

When the objective is identified and relevent emperical information is gathered, the next step is to determin the relative importance among the criteria that is under consideration. This process involves giving a specific weight to each criteria based on its percieved importance. This step establish a hierachy, it ensures that the most significant criteria is given appropriate attention. This is done by giving each criteria a relative importance in the Saatys scale 1-9 as shown in table 1, which a person decides. It should be noted that the sum of each row is computed, this is used for later calculations.

	Cost	Support	Flexibility
Cost	1,00	2,00	3,00
Support	0,50	1,00	2,00
Flexibility	0,33	0,50	1,00
Sum	1,83	3,50	6,00

Evaluate the performance of each alternative with respect to each criterion

The alternatives are assesed by making a pariwise comparision, just like the previous step. For this step the alternatives are compared against eachother with respect to each criterion the, where they are given a relative importance just like earlier, which a person decides. they are then compiled into tabels, shown below:

Alternatives with respect to cost
	Company 1	Company 2	Company 3
Company 1	1,00	7,00	2,00
Company 2	0,14	1,00	0,25
Company 3	0,50	4,00	1,00
sum	1,64	12,00	3,25

Alternatives with respect to support
	Company 1	Company 2	Company 3
Company 1	1,00	5,00	3,00
Company 2	0,20	1,00	0,50
Company 3	0,33	2,00	1,00
Sum	1,53	8,00	4,50

Alternatives with respect to flexibility
	Company 1	Company 2	Company 3
Company 1	1,00	0,11	0,13
Company 2	9,00	1,00	1,00
Company 3	8,00	1,00	1,00
Sum	18,00	2,11	2,13

In order to give a relative weight to each criterium, the matrices are normalised. This is done by dividing each value with the sum of the column value. Afterwards the priority is calculated, this is done by taking the sum and dividing with the number of elements, 3 in this case:

Criteria Normalised
	Cost	Support	Flexibility	Priority
Cost	0,55	0,57	0,50	0,54
Support	0,27	0,29	0,33	0,30
Flexibility	0,18	0,14	0,17	0,16

The values calculated under priority have a meaning in AHP, the values represent the relative importance of the criteria to the overall goal. In this case the company have decided that flexibility have a importance of 16% (this is the priority calculated in the above table).

Preform consistancy test

When preforming the consistancy the following is computed:

1. The largest eigenvalue, λ_max, of the matrix is calculated
2. The Consistency index (CI) and the consistency ratio (CR) is calculated

Math software, like maple, was used to find the largest eigenvalue of the matrix. The consistency index is calculated with the following formula:

$CI =\frac{\lambda_{max} - n}{n-1}$

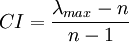
where n is the number of elements. RI is is called the random consistency index, to finx the consistency ratio the CI is divided by the RI. The consistency ratio can be calculated with the following expression:

$CR =\frac{CI}{RI}$

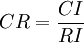
The values for RI is presented below:

Consistency of random matrices
matrix order	1	2	3	4	...
RI	0.00	0.00	0.52	0.89	...

The consistancy test is preformed for the criterum matrix,cost matrix, support matrix and flexibility matrix:

Consistancy test
	Criterium	Cost	Support	Flexibility
Lambda_max	3,009	3,002	3,004	3,002
CI	0,004	0,001	0,002	0,001
CR	0,008	0,002	0,003	0,001

Calculate the global priority of each criteria and ranking

The AHP ranking
	Cost	Support	Flexibility	Global Priority	Rank
Company 1	0,602	0,648	0,056	0,526	1
Company 2	0,082	0,122	0,481	0,160	3
Company 3	0,315	0,230	0,463	0,314	2

Critique of the AHP method

NOTE TO ME: look here

Inplementation of AHP method in organisations

NOTE TO ME Look at the conclusion