Feasibility risk assessments of transport projects using Monte Carlo-simulations

Abstract

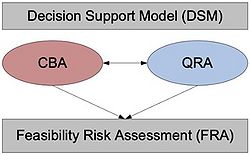
A common way of assessing the feasibility of an infrastructure projects (e.g., road or rail) is through a cost benefit analysis (CBA), resulting in an overview of the cost and benefits/ consumer surplus as the Net present value (NPV) or Benefit cost ratio (BCR) of the project. Values which can be compared to other projects/alternatives. The result of a CBA though relies on a single value where all assumptions, estimations and calculations are reduced to a single number. It can thus be difficult to describe the certainty of the result and due to the complexity of infrastructure projects a risk of cost overruns and overestimations of benefits are historically likely to occur . One way to challenge this problem is to perform a Feasibility risk assessment (FRA) moving from a single point result to an interval result.

One FRA technique trying to cope with some of the shortcomings of CBA are a stochastic approach based on Monte Carlo simulations using reference classes. Also called reference scenario forecasting (RSF). The idea of using reference classes is to gather all possible information regarding already implemented infrastructure investment projects, which thus can be used to provide a background for evaluation of future projects and identify probability distributions that can model the uncertainty of the project impacts. .

The result of the FRA using Monte Carlo simulation is a certainty graph and/ or certainty interval providing information about the certainty of achieving e.g., a BCR of at least one. That is potentially valuable information for decision makers describing in how many cases or how large the certainty is of obtaining a project that is feasible.

Reasoning behind and optimism bias

Decision support model towards the feasibility risk assesment

In order to get a social, environmental, and economical acceptance of an infrastructure project an assessment of the impacts is necessary. This includes travel time savings, emissions, accidents etc. as well as construction and maintenance cost summarised in a Cost Benefit analysis. The CBA has the advantage that it through the provided set of criteria sums up all aspects of the decision problem to one single monetary value and make the variety of projects comparable and consistent.

This though may also be considered a weakness as the methodology might be seen as a “black box” reducing all considerations and assumptions to one single value. Furthermore, the unit pricing principles and modelling of impacts involves uncertainties due to the unknowns of the future . Thus, the CBA only provides a single guesstimate on the feasibility of the project.

Megaprojects are inherently risky due to long planning horizons and complex interfaces and a systematic tendency to overstate some of the major impacts, such as user benefits and construction cost are demonstrated. This is also known as “optimism bias” where lessons learned are likely to be neglected with a with a common belief that the future will be better than the past and that ‘the same mistake won’t happen twice'. The traditional way of handling the above-described uncertainties is through a risk analysis. Here, the undesirable effects that the subsequent activities may impose are identified and quantified in a risk matrix and mitigation measures are determined. Each single project is thus handled as a unique project identifying what may go wrong within this context. The traditional Risk analysis of course gives some useful insights and provides the decision maker with a method by which he/her can gain information on the totality of any future outcome. By adding a quantitative risk analysis (QRA) it provides the possibility to differentiate the feature of risk information in terms of outcome by probability distributions </ref>. While the CBA is appealing to its adaptability and flexibility it often applies a ‘false sense of security’ where underlying model uncertainties are somehow forgotten. Complementing the CBA with a QRA in a “feasibility risk assessment” (FRA) thus provides additional knowledge on the viability of a project and handle the uncertainties present in the decision making by moving from a single point result in the CBA to an interval result with a corresponding probability.

Application

When applying the QRA and the subsequent FRA a common mistake is to choose an inadequate distribution. Several research studies have been made to find suitable distributions describing different transport impacts as construction cost, travel time savings, accidents etc. But in the end, it all comes down the level of knowledge about realised impacts of already implemented projects.

Choosing distribution

• The importance of choosing the right distribution

• Deriving probability distributions for risk modelling of transport projects

• Usage of a project database and reference classes - This includes benefits as e.g., travel time savings and construction cost

Monte Carlo simulation

• Briefly, what is Monte Carlo simulation

• Running the Monte Carlo simulation

Certainty graph

• Example of FRA outcome and how to interpret.

Limitations

Project database and reference classes

• The similarities between projects

Post analysis usually made on successful transport projects.

• Lack information on overestimated user-benefits

Other application areas

Project scheduling

• Optimism bias also applies to time planning.