Benefit Cost Ratio (BCR)

Abstract

This article discusses the application of the Benefit Cost Ratio (BCR) method in the Cost Benefit Analysis. The Benefit Cost Ratio is a profitability indicator, and it is the ratio of the present value of the benefit of the project to the present value of the cost. It is usually used to summarize the results of the cost benefit analysis (CBA) during the financial appraisal of a proposed program, project or portfolio. BCR indicates if the project is feasible or not, meaning the higher the BCR, the more attractive the risk-return profile of the project/asset. If the BCR value of a project is less than 1, the project's costs outweigh the benefits, and it should not be considered viable. Calculating the BCR of an asset or project is comparatively simple. In addition, the ratio considers the discount rate, hence the time value of the money.. Despite the fact that BCR is a tool to show the attractiveness of a project or an asset, cannot simply be the only determinant of a project's feasibility.

Initially, this article discusses the origin of the Cost Benefit Analysis and BCR. Then, it focuses on the formula for the calculation of the Benefit Cost Ratio and how it considers the time value of the money. Next, there is a comparison between BCR and other CBA methods. After that, the article introduces other formulas and applications of the BCR. Finally, it discusses the advantages and the limitations of the Benefit Cost Ratio.

Cost Benefit Analysis

Cost-benefit analysis (CBA) is a method of economic assessment that seeks to quantify the positive and negative impacts of a proposed decision or project. The technique has been used for centuries, with the earliest known examples dating back to the 1700s. However, the use of CBA were mandatory only after regulations were established by the US government in the 1930s CBA is often used to determine whether or not a proposed decision or project is worth investing in. It is also used to compare different options or to determine which option will provide the greatest benefit to its stakeholders. One of the earliest applications of cost-benefit analysis was in the transportation sector, where it was used to evaluate the feasibility and desirability of public infrastructure projects.

In the 1960s, there were economists such as Kenneth Arrow, Milton Friedman, and Richard Musgrave, who supported that CBA could be an important method for evaluating the efficiency of government programs.

After that, CBA was refined over the next decades due the advent of computers and still more sophisticated prediction modelsand is widely used in a variety of fields, including environmental regulation, health care, and transportation planning.

The last years the goal is to link CBA with other methods (hard and soft operation research techniques) and setting a focus on wider impacts, stakeholders and robustness. It is widely accepted that the use of only cost-benefit analysis (CBA) may not be sufficient to fully evaluate the complex social, economic, and environmental impacts of a particular decision or policy. As a result, there has been increasing interest in integrating CBA with other methods, such as hard and soft operations research techniques, as well as other forms of economic analysis. Moreover, there has been a focus on broader impacts beyond just the monetary costs and benefits, such as social and environmental impacts, and taking into account the perspectives of various stakeholders. This is often referred to as a "multi-criteria decision analysis" approach.

What is BCR?

The Benefit Cost Ratio is a profitability indicator, and it is the ratio of the present value of the benefit of the project to the present value of the cost. It is usually used to summarize the results of the cost benefit analysis (CBA) during the financial appraisal of a proposed program, project or portfolio. The origins of BCR can be traced back to the early 20th century when economists and engineers first began developing methods to evaluate the costs and benefits of public infrastructure projects. One of the earliest known applications of BCR was in the United States in the 1920s, when the Bureau of Public Roads began to use it to evaluate the economic benefits of road construction projects. BCR began to be used as more in the 1930s and 1940s, when economists and engineers needed to refine and standardize methods for estimating costs and benefits.

Today, the BCR is widely used by the public and private sectors to assess the economic viability of various projects and investments, such as transportation infrastructure, power generation facilities and public health initiatives.

BCR is another way of comparing the present value of a project’s costs with the present value of its benefits. If the value of BCR of a project is greater than 1.0, the project is expected to have also a positive NPV and to have an internal rate of return (IRR) higher than the discount rate used in the calculations. When the BCR has a value equal to 1.0, indicates that the NPV of expected profits equals the costs. If BCR of a project is less than 1.0, the project's costs outweigh the benefits, and it should not be feasible.

Time value of money

Benefits and costs have a higher value today than tomorrow. The time value of money is a basic financial concept used to calculate the present value of an amount of money today compared to its future value. This concept is based on the idea that money has a time value because it can earn interest over time. In other words, a dollar received today is worth more than a dollar received in the future due to the potential to earn additional.

There is a need for discounting when comparing any flow of funds (costs and revenues or benefits) over time. To consider the process of discounting in practice, consider two investment projects, A and B. The net cash flows of these projects are given as:

The values of each year need to be discounted to calculate the present value, and there is an example for these calculations making the usual assumption that the discount rate is constant from year to year.

Discount Factors for 10% and 15% Discount Rates

Discount Rate

The discount rate is the rate of interest used to calculate the present value of future cash flows in economic appraisals. It is used to discount the expected future cash flows to their present value. The discount rate used in economic appraisals is usually determined by the current level of interest rates. Discounting is used when monetary values are distributed in time and these values should be added together in a specific year. A simple way of understanding discounting is to see it as a weight with this weight (1+i)^t determined as a function of t and the discount rate is i, as it can be seen below:

$\frac{B_t}{(1+i)^t}$

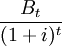
How to Calculate BCR?

$BCR = \frac{\sum_{t=0}^n \left(\frac{Bt}{(1+i)^t}\right)}{\sum_{t=0}^n \left(\frac{Ct}{(1+i)^t}\right)}$

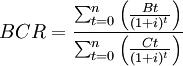
Where:

t: The calculation period in years

Bt: Benefits in year t

Ct: Costs in year t

i: The discount rate

Examples

Example 1

In this section, there will be an example of how BCR can be calculated in a scenario. A company decides to lease the equipment needed for a project for $50,000 rather than purchasing it. The discount rate is 2%, and the renovations are expected to increase the company's annual profit by $100,000 for the next three years.

$BCR = \frac{\sum_{t=0}^n \left(\frac{100000}{(1+0.02)^t}\right)}{\sum_{t=0}^n \left(\frac{50000}{(1+0.02)^t}\right)}$

$BCR = 5.77$

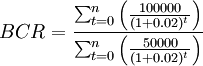
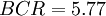
In this example, the BCR of the project is 5.77, which indicates that the project is feasible. Moreover, the company could expect $5.77 in benefits for each $1 of costs.

Example 2

The government is considering building a new highway, and they want to calculate the Benefit-Cost Ratio (BCR) of the project. They estimate that the construction cost will be $100 million and the highway will generate 30 million in benefits for each year over the next 4 years. The discount Ratio is 3%.

$B = \frac{30,000,000}{(1+0.03)^1} + \frac{30,000,000}{(1+0.03)^2} + \frac{30,000,000}{(1+0.03)^3} + \frac{30,000,000}{(1+0.03)^4}$

$B = $111.78 \text{ million}$

$BCR = \frac{B}{C} = \frac{111,780,000}{100,000,000} = 1.1178$

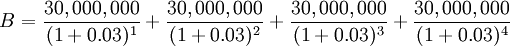
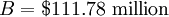
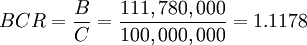
This means that for every dollar spent on the project, there will be $1.1178 in benefits over the next 4 years. A BCR of greater than 1 indicates that the project is economically viable.

Comparison Between BCR and NPV

BCR and NPV are two different methods of financial appraisal. BCR measures the ratio of benefits to costs, while NPV measures the present value of future cash flows. Both methods measure the profitability of an investment with different methods. BCR focuses on determining ROI, while NPV takes into account the present value of future cash flows.

Comparing or ranking two or more projects, again assuming no budget constraint, the BCR decision-rule can give incorrect results. For example, comparing two different projects A and B , where:

For the projects A and B, the BCR value is 1.67 and 1.78, respectively. However, using the NPV decision-rule would place A (NPV=40) above B (NPV=35). In this situation the NPV decision-rule would be the correct one to consider for ranking purposes, unless there is a budget constraint.

Other formulas of CBA

1. Payback Period BCR = Initial Investment / Annual Cash Inflow

2. Return on Investment BCR = Annual Net Income / Initial Investment

3. Net Present Value BCR = Net Present Value / Initial Investment

4. Internal Rate of Return BCR = Internal Rate of Return / Discount Rate

5. Profitability Index BCR = Present Value of Future Cash Flows / Initial Investment

Advantages of BCR

1. The BCR translates the absolute amounts of benefits and costs into a ratio.

2. It is a simple method and a good starting point in determining if a project is feasible or not.

3. For the calculation of BCR the time value of money through the discount rate is considered.

Limitations of BCR

1. The main limitation of the BCR is that it reduces a project to a simple number when the feasibility of an investment or a project relies on many factors and can be undermined by unforeseen events.

2. The calculation of BCR of a project depends in many assumptions. For example, an incorrect discount rate would lead to a flawed ratio.