Utilizing Value Functions for Evaluating the Performance of Project Alternatives

Value functions are a value measurement approach that is often used in multi-criteria decision analysis (MCDA), which strives to improve decision-making. MCDA is a decision support tool used to assess solution alternatives based on a wide range of criteria, which can be both monetized and non-monetized. To assess the various criteria, value functions can be utilized to assign value to the various alternatives fairly. Value functions are thus a mathematical model that translates stakeholder preferences into a measurable scale.

Value functions are especially useful when comparing different choices (this can be solutions, projects, or other decision-related alternatives) as it converts the different choices, or evaluation criteria, into a common scale for a fair and less biased comparison as value functions assign a specific value to each solution alternative, creating a preferential structure. Consequently, value functions can assess various aspects of a solution and give a concrete value to each solution alternative to support a less biased decision basis.

As the tool can support various decision-makers in their choices, it can be used in all sorts of decisions, depending on how the function is defined. For use in portfolio management, the value function should be defined based on how well a given project meets the organization’s strategic goals. The project which performs best on the value function(s) will thus display the project that is most beneficial to the portfolio. Likewise, program managers can use value functions to identify projects which best fulfill the program’s objectives, to find the project that best balances competing demands and possible trade-offs, and to find the optimal project pool. Finally, it can be used in projects to find the best alternative solution or support the resources allocated to project activities.

This article gives an overview of what a value function is and a guide on constructing various value functions. There will also be a discussion on how and when to use value functions and their application in program, project, and portfolio management. Finally, this article will discuss some of the limitations of value functions and suggest alternative tools for when value functions are not applicable or practical.

Value Functions

Value functions are a mathematical model which can translate stakeholder preferences and ideals into a less biased scale. Value functions should be used when the decision maker needs to choose a specific solution from a pool of solution alternatives. By creating a value function the decision maker will be able to identify the solution that will give the greatest reward. This is done by combining the indexes of all the alternatives into a measurable index of preferability. Value functions can be used to determine the value of a thing by looking at both tangible and intangible aspects. Thus, it properly evaluates all relevant aspects of a project, concept, or idea and their alternatives. A value function considers the value of a solution alternative on each of the criterions used in the decision basis. The primary function of the value function is to support the stakeholder in assigning value to each alternative, and then use the weight of each criterion to find the final benefit of the solution alternative. It should be noted that for each criterion a value function should be created. Value functions are useful when evaluating and comparing similar solution alternatives, as they assign a specific value to each solution alternative, creating a preferential structure. Often when evaluating a solution alternative or project several value functions are used, one for each of the performance criteria (also known as key performance indicators (KPIs) ). From these each solution alternative or projects performance can be assessed through the specific score/value that the solution alternative or project obtains on the value function scale. As value functions are a mathematical expression, they follow axioms, the most essential are that the preferences expressed by value functions should be coherent, thus they must be transitive and complete. This means that if project a is better then project b, and b is better then project c, then project a is better than c. It also means that either one project is better than the other or they are indifferent (project a is equally good as project b). Thus an alternative is only preferred to another alternative if its score on the value function is better than the other. If the scores are the same, then there will be indifference between the alternatives, meaning that they perform equally well.

Types of value functions

The most used value function model is the additive model:

$V(a)=\sum^n_{i=1}w_i *v_i(a)$

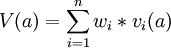
Here V(a) refers to the total value of the solution alternative, 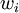$w_i$ refers to the weight (the importance) of criteria i, and $v_i$ refers to the value of the criteria for the solution alternative. The additive model is easy to use, and especially easy for stakeholders to understand, making it the most used value function. In decision making it is essential that the stakeholder understands the process and thus the indicated solution preference. The additive model looks at each criterions impact on the complete value. It is also easy to change, add, and remove criteria from the model.

An alternative to the additive model is the multiplicative model:

$V(a)=\prod^n_{i=1}v_i(a)^{w_i}$

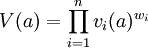
The multiplicative model is harder for stakeholders to understand, however it better accounts for interdependencies between the criteria on the solution alternative. Thus it is better suited for finding an alternative which performs well on all criteria. This form of value function is best suited when the weights for each criteria is well known. Once a value type is decided upon there are various ways of creating the value function. Two of these are divulged here, the bisectional method and the difference method.

The bisectional method

The bisectional method is a direct method which needs input from the stakeholder. Here the stakeholder will identify the two end points of the value function, so the maximum and minimum value an attribute can have (this will depend on the chosen scale, see the scales section below). Then the stakeholder will identify where, between the two endpoints, the value is half, so when would the stakeholder consider a solution to have half the value of the maximum outcome. As an example, let’s consider a program where an objective is reducing emissions. When choosing a project for this program it is thus beneficial to consider how it contributes to the reduction of emissions. The full 100% value (from a global scale) would be that the project has the potential to remove emissions completely and a value of 0% (for this criterion) would be that if it does not reduce emissions in any way (as it is decided to not continue with projects which go against the program objective). Then using the bisectional model the stakeholders will decide when half the value is reduced, so where is the solution valued half as much as the complete emission reduction is valued. So if the stakeholder has to reach certain emission reductions, they would value a larger reduction far more than a small reduction, placing the halfway point closer to the 100% value. Then the same practice is done for the 75th and 25th quartile. Where the 75% value is given between the 50% and 100% marker, and the 25% value is given between the 0% and 50% using the same logic as previously. Once these five points have been identified it is possible to sketch out the value function and then assign value to the alternatives based on the function.

• • • A depiction of the value function example will be added here***

The difference method

An alternative to the bisectional method is the difference method. Here the stakeholder is presented with a segment of the different values and has to rate them. Here the ranking will provide an idea of the value function, which can be sketched out. Using the example above, it is possible to use the difference model by taking the 0 CO2 emission and the current emission (lets say it is a 1 ton ) then using the difference method the difference between these would be segmented into a n categories. For simplicity’s sake it is here divided into four categories: 0-250 kg, 251-500 kg, 501-750 kg, and 751-1000 kg. Then the stakeholder will rate theses categories with an increase in value, lets say the larger the reduction the better, as they wish to be frontrunner, and reach their emission reduction targets. Then the stakeholder will rank the 751-1000 reduction as the most important, then the 501-750, the 251-500 and finally the 0-250 will be valued the least. Once these preferences have been found it is possible to sketch out the value function and then assign value to the alternatives based on the function.

• • • A depiction of the value function example will be added here***

Scales

To assign value to a value function through the methods above it is necessary to define the scale. Once a scale has been defined it is possible to assign value to the alternatives, and later find the weights of each criterion to get the final value. There are two scales, local and global, the former is defined based on the current alternatives, while the other is based on a broader range of possible alternatives. This means that the local scales outer boundaries are based on the best and worst performing alternatives, where the best will get a value of 100 and the worst will get a value of 0. Meanwhile the global scale will assign the best value to the best possible outcome, and the worst to the worst possible outcome. The global scale should for practical reasons only consider reasonable extremes. An example of the global scale could be the wish to reduce burning accidents, from a project stand point the best performance would then be a solution which ensured that no burns accidents could happen, while the worst performance would be a project which increased the current burning accidents, or which did not improve at all. There are different benefits to both the local and global scale. The local scale allows for easier and quicker assessment of the alternatives and is beneficial if a rough estimation is fine for the criteria, and if time resources are limited. The global scale, while more time-consuming, is more generic, after creation it will be easier to access new alternatives.

Application

Value functions can be used whenever a variety of criteria must be taken into consideration when making a decision. Thus, they can be favorably used in project, program and portfolio management to support the decisions. How to formulate value function can vary as much as the setting it is applied in. However, the procedure is quite similar. The most essential aspect of creating value functions is to ensure complete transparency for the decision-mkaer, only when the decisionmaker participates in the process will they be able to effectively understand and use the output of the value functions. This is a natural part of the process, as the value function concept expressed here is focused on supporting various multi-criteria decision analysis techniques, which to various degrees include stakeholder opinions and input. Value functions are created at different stages of various MCDA techniques, thus they can be hard to differentiate. What is essential for all application however, is to have well-defined alternatives and criteria. Once a decision-maker has identified said alternatives and criteria they will be able to define the value functions.

The first step to creating a value function is to define scale. As mentioned previously the decision maker must decide whether this scale should be representative for current and future use, in which case it should be global. Otherwise, if the scale should be easy to create for a quick comparison then the decision maker should use a local scale. Once one of these scales are chosen, a measurable criterion scale should be defined. This means that it should be possible to measue the different solution alternatives performance on the criteria directly. Such a scale could be cost, time, or weight as seen in the emission example. This should be a well-defined scale, if it is not possible to find an suitable scale, then a qualitative scale can be constructed, though this leaves room for further subjectivity and confusion. For more information on this please see Belton and Stewart. The next step will be to decide on what method to use when creating the value function. The choice of which mainly depends on stakeholder and decision makers preferences.

Using the methods described above it is possible to understand the stakeholder and decision makers preferences by attaining their preference structures. It can be beneficial here to ask the decision maker what they value most or to obtain certain goals or milestones they have and link it to the output of the project, program and portfolio. By matching criteria to the stakeholders objectives it can help measure where most value should be assigned. Sometimes it is more valuable to reach a target, and anything above this target is merely a bonus, while at other times it is more beneficial to get as much or little as possible. This will have to be an individual assessment for each criterion and thus each value function.

It can be a help to discuss the flow of the value function with the decision maker and stakeholder. A value function can have three different looks; monotonically increasing against the natural scale, monotonically decreasing against the natural scale, and non-monotonic. Value functions which is monotonically increasing against the natural scale assigns the most value to the solution alternative that has the highest scale value. For example, the higher the perceived profit the better the value. Oppositely a value function which is monotonically decreasing against the natural scale assign the most value to the solution alternative that has the lowest scale value. For example, the lower the perceived resource consumption (time or money) the better the value. Non-monotic value functions have interspaced peaks, meaning that the highest value and lowest value is not at the endpoints. An example could be project integration in programs, as there might not be a linear relationship as there is a difference between integrating a few highly integratable projects and many less integratable projects.

• • • Depiction of all three will be inserted here***

Generally non-monotic value functions should be avoided, as value functions should strive to be as linear as possible. If the created value functions are far from being non-linear it is possible that the criteria should be redefined. However, a bit un-linearity is to be expected to ensure that the problem is not oversimplified. The bisectional and difference method both assume that the value function is monotonically increasing or decreasing against the natural scale. After having created the value function using the difference or bisectional method, the value function is ready for determining the value of each of the solution alternative. This can most easily be measured visually by taking the solution alternatives performance value and measuring it up to the value functions value axis. When all solution alternatives have been measured against each criterion it is possible to find the aggregated results by using the formulas above. Hereafter each solution alternative will have a specific value, the higher the value the more beneficial the solution.

Limitation

While value functions can be useful, they are not applicable everywhere, and it is essential to be aware of their limitations. For one value functions are less suitable when there is limited data and where it is hard to connect reliable assumptions from the stakeholders. Besides the applications there are also certain issues with the method that any user should be aware of. First of value functions are subject to objectivity and bias. Despite the mathematical properties, all preferences and inputs are based on subjective opinions. It is thus essential to include several stakeholders opinions as the results can vary based on stakeholders preferences towards various solution alternatives and criteria. The overall solution derived from the aggregated value functions will also be subject to uncertainty if all criteria have not been identified as this can misrepresent the complete solution.

When working out the value functions there is also the issue of human input. As mentioned previously value functions use human input, thus they are subject to human errors. This means that there can be an inconsistent preference structure. As mentioned previously some non-linear preferences are allowed, but to much can skew the results. It is thus necessary to ensure that the value functions follow the axiom of transitivity, and have a linear tendency.

Another limitation to be aware of is the understanding and interpretation of the finished value function. The decision maker must understand the procedure and the results properly. They must be comfortable with the solution and trust it enough to take the results into account, otherwise the work will not be used. It is also essential for the stakeholder to understand the procedure otherwise their preferences and weights will not be as clear and trustworthy. When these limitations and issues cannot be handled properly other alternatives for determining the weight of the criteria. Such alternatives could be construction of qualitative value scales, or direct rating of the alternatives.

References

von Winterfeldt, D., and Edwards, W. Decision Analysis and Behavioral Research. Cambridge University Press

Belton, V., and Stewart, J.T. Multiple criteria decision analysis: an integrated approach, Kluwer Academic Publishers, London.

Stewart, T. J. Use of Piecewise Linear Value Functions in Interactive Multicriteria Decision Support: A Monte Carlo Study. Management Science 39, pp. 1369-1381, Informs.

Stewart, T. J. Robustness of Additive Value Function Methods in MCDM. Journal of Multi-Criteria Decision Analysis 5, pp. 301-309, Wiley.