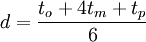Dealing with schedule planning by the Critical Path Method

Developed by Kasper Kjær Rasmussen

A project usually involves a large amount of activities and tasks needed to be done. Even for the most experienced project managers it can be a bit of a challenge to control the huge amount of complexity in a project. By mastering the concept of planning a schedule a project can not only be more structured. Sufficiently planning can reduce the overall costs and limit the time duration of the project. The Critical Path Method is one of the tools a project manager can use to plan the project in the best possible way. The basic idea behind the method is to identify all the dependencies and interactions between the tasks and point out the essential tasks that drive the project timeline

This article analyses the Critical Path Method. It takes a closer look at how to use the method and discus the advantages and limitations of the method.

The article starts by clarifying the idea behind the method, and then showing the general application of the method with an illustrating example. This is carried out with an example by hand as well as by a more general approach with use of digital tools. The article then reflects on the use of the method. This is done by looking at the limitations of the Critical Path Method and comparing the method to other approaches of project scheduling. Furthermore, suggestions to improve the method are discussed.

The idea behind the method

A project has several tasks that needs to be done in order of the project to progress. The tasks can have dependencies on each other and some of the tasks needs to be completed before others can start. The tasks can also be dependent in a way that they should be done at the same time. The dependencies of the tasks can be divided into three main cases .

• Technical dependencies - Beams cannot be placed without any supports and the construction of the beams therefore depends on the construction of supporting columns.
• Organisational dependencies - Walls can be painted before the installation of the roof is completed, but the risk of damaging the painting by dust and other things by this schedule planning is high. It therefore might be a good idea to reverse the order of the two tasks.
• Spatial dependencies - The installation of electricity and water pipes does not have any technical dependencies, but they often require the same space. In other words, they have spatial dependencies and therefore needs to be completed parallel or close to each other.

For even small projects the amount of complexities of these dependencies can easily be high. To handle the dependencies a technique known as the Critical Path Method has been developed. The method was developed separately during the late 1950’s by the U.S. Navy and the American company DuPont . The basic idea behind the method is to identify all the dependencies and interactions between the tasks and point out the essential tasks that drive the project timeline. By doing so, the planning can be optimized to know which tasks that can be delayed and which ones that will affect the whole time of the project if not completed on time. The minimum length of time to complete the project is identified as the length of the sequence of tasks defining the critical path. Delaying any of the tasks on the critical path by either starting or finishing a task later then planed the whole project will be delayed. If any tasks outside the critical path are delayed, it would not affect the project, unless the delays are so extreme that these tasks become the new critical path. To reduce the time duration of the project, the project manager then knows which sequence of task that should be focused on, because more resources on tasks which are not on the critical path, will not affect the overall duration of the project. It is important to realise than even though many projects have only one critical path, multiple critical paths can occur.

Application and guidance of the method

In the following section the application of the method will be described. This is done in a general manner alongside with an illustrating example. The essence of the application is to fill out a sequence of critical path descriptors, as seen in Table 1. Based on the sequence of task descriptors, the critical path can be identified .

Table 1: Critical path task descriptor

Step 1: Identifying the dependencies

To apply the method all the dependencies of the tasks needs to be identified. The network of dependencies can then be illustrated as seen in Figure 1. The duration estimates of the tasks will be explained later in this article, but for now the durations are shown with no comments. The durations are given in days, but the time unit is in principle not important for the example.

Figure 1: Project network of dependencies

Step 2: Calculating the earliest start and finish

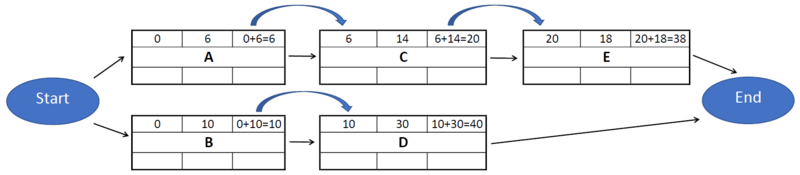
As soon as the dependency network is established, the earliest start and the earliest finish of every task in the project can be calculated. This is done by carrying out a forward pass computation. The earliest start of a task is given as the earliest finish of the previous task in the dependency network. This is because a following task cannot begin before the previous has ended. The earliest finish is given as the sum between the earliest start date and the duration of the respective task. For the given example, the earliest start and finish of all the tasks are shown in Figure 2.

Figure 2: Project network of dependencies with forward pass computation

Step 3: Calculating the latest start and finish

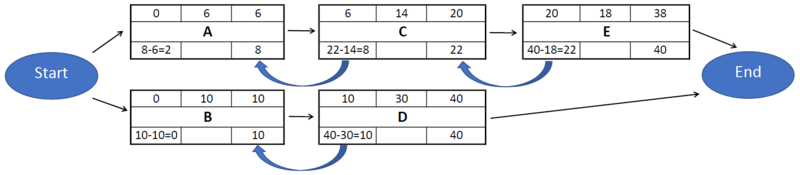
Based on the computed dates of the earliest start and finish the latest start and finish can be calculated. This is done in a similar way as shown in Step 2, but this time by backward pass computation. The latest finish of the last task in a sequence is set equal to the earliest finish of the last task in the project. The latest start is then calculated as the difference between the latest finish and the duration of the task, as seen in Figure 3.

Figure 3: Project network of dependencies with backward pass computation

Step 4: Calculating the slacks of each task

The allowable slack in the tasks can then be calculated. The slack for each activity is given as either the difference between the earliest start and finish, or the difference between the latest start and finish. The slacks in all the tasks in the example are shown in Figure 4.

Figure 4: Project network of dependencies with slack computation

Step 5: Identifying the Critical Path

The critical path can then be identified as the sequence of tasks without any allowable slack. For the illustrating example the critical path is the sequence of task B and D, as shown in Figure 5. Since there are no slack in those tasks the earliest and latest finish of the tasks are equal. A delay in any of them will extend the total duration of the project. It is noted that the critical path not necessarily is the sequence with most tasks. The critical path is the path that takes the longest time to complete.

Figure 5: Project network of dependencies with the critical path identified

Digital tools

For large projects the level of complexity is enormous and it will take long time to establish the critical path by hand. It is therefore obvious to use a digital tool to speed up the calculations. One of the most used programs in schedule planning is Project 2016 developed by Microsoft. In the following section, Project 2016 is used to compute the critical path for the illustrating example, dealt with in the previous section .

When Project 2016 is opened and an empty template is chosen, the screen will look like the shown in Figure 6.

Figure 6: Start up picture in Project 2016

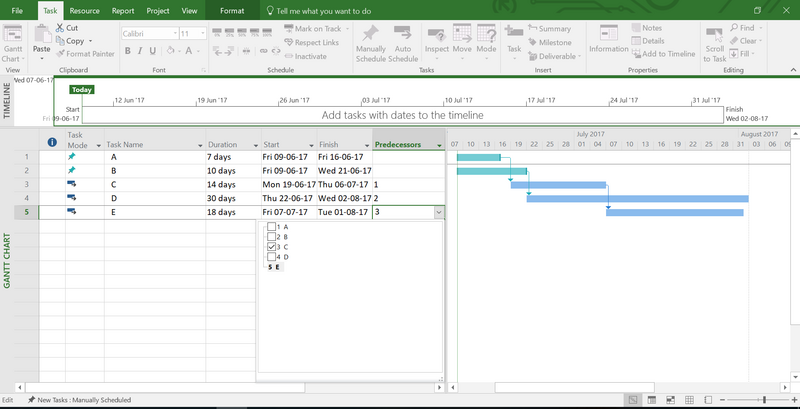
The task names, the durations of each task as well as the dependencies between the tasks should afterwards be defined. In the left side of the worksheet, a column describing the task mode is given. This column can either be set to manually scheduled or auto scheduled. The name of the task is then given and the durations are inputted. The durations can be inputted in all time units, but the standard is days. The dependencies between all the tasks are defined in the column Predecessors. By double clicking in the Predecessor column for each task the dependencies can be marked as shown in Figure 7. After all the tasks are inputted a Gantt Chart is shown in the right side of the window.

Figure 7: Project network of dependencies in Project 2016

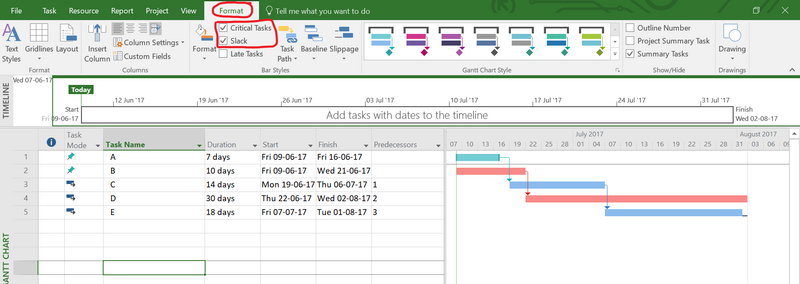
The critical path and the possible slacks for tasks outside the critical path is found. In the menu line go to Format and check the boxes “Critical Tasks” and “Slack”. The critical path then appears as red boxes, as seen in Figure 8.

Figure 8: Project network of dependencies with the critical path identified in Project 2016

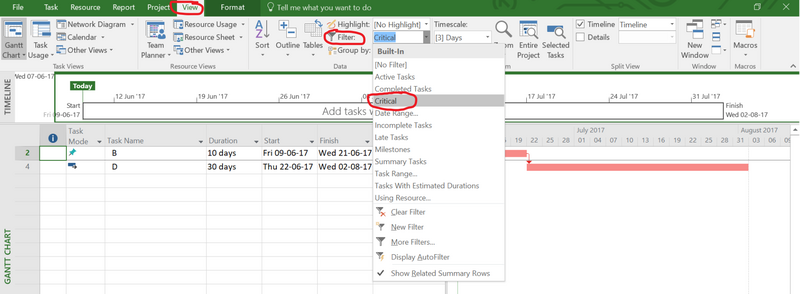
For small projects, it is easy to have an overlook of the entire project. For larger projects, on the other hand, there are so many tasks and dependency relations that it can be difficult to identify the critical path, even though the critical path is highlighted with red. A feature in Project 2016 handles this issue. If one goes into the View tab and click the Filter box, and afterwards chose the option “Critical”, then only the critical path is shown as illustrated in Figure 9.

Figure 9: Critical path identified in Project 2016

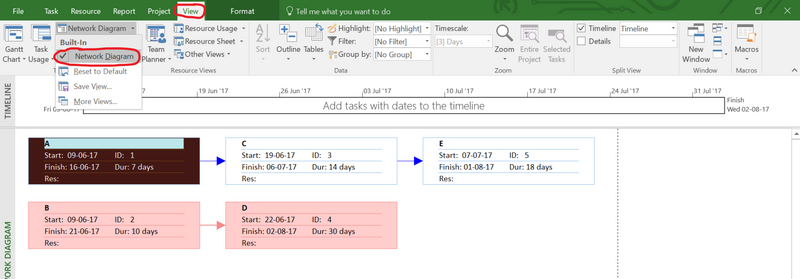
Another useful feature can be found by clicking the View tab again and choosing the option “Network diagram”. The entire network diagram is then shown, as illustrated in Figure 10.

Figure 10: Project network of dependencies with the critical path identified in Project 2016

Estimating the time duration

One of the most important assumptions regarding the Critical Path Method is that the time durations for each task are known. When estimating the time durations there are generally two sources of knowledge .

• The time estimates can be based on measuring from previous projects with equal or similar tasks
• The time durations can be estimated by the people in charge of the respective tasks.

It is important to accept that the time estimates can be very uncertain. Unforeseen events such as the weather, material shortages or a flu epidemic can easily extend even the most reliable time estimates. In the estimations of the time durations it is therefore obvious to use probabilistic methods. Several probabilistic approaches of time estimations exist. One of the most known approaches is PERT, which are developed by the U.S Navy. PERT operates with three time estimates and it is assumed that the distribution between the three estimates follows a Beta distribution . Defining the most optimistic duration as 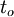$t_o$, the most likely duration as 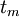$t_m$ and the most pessimistic duration as 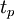$t_p$, the expected duration of a task can be estimated to be

$\begin{align} d & {} = \frac{t_o + 4t_m + t_p}{6} \\ \end{align}$

Speeding up the time schedule

Everything in a project has costs. The direct costs are a result of labours, materials and equipment. The indirect costs are things like maintaining facilities and sometimes they are also a result of penalties there are incurred because a deadline has been missed. Time-Cost models deals with the case that it might be more cost-effective to invest in more resources in order to speed up a task rather than delaying the whole project. This section deals with a Time-Cost model called The Time-Cost Trade-Off . The section describes the basic idea and application of the method and gives a small example.

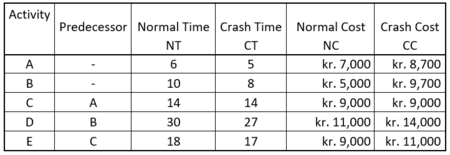
The basic idea behind the method is that when additional resources is added it might be possible to reduce the time duration of a task. This is known as crashing the project. It is common sense that when additional resources are added the costs to the tasks are increased. The method distinguishes between the normal time and cost, which are the duration time and cost that was originally planned, and crash time and cost, which are the time durations and cost by reducing the time schedule. Based on these values the cost per day to expedite a task can be computed. It can afterwards be evaluated whether the extra costs by crashing the project are economical beneficial for the project.

Let’s assume the same task and dependency relations as given in Figure 5. The job is to reduce the time schedule by two days. The following Time-Cost data shown in Table 2 has been estimated by the project manager in coordination with the contractor.

Table 2: Time-Cost data

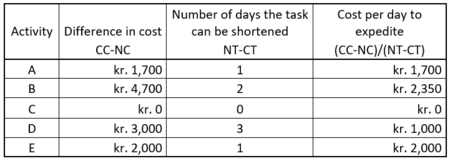
From the data in Table 2 the cost per day to expedite the project can be computed as shown in Table 3.

Table 3: Time-Cost calculation

As mentioned earlier in this article, the time duration of the project can only be affected by reducing task times at the critical path. These are task B and D for the shown example. The overall time must be reduced by two days. It is seen that it is cheapest to reduce task D by two days rather than reducing task B with two days. To reduce task D with two days, the overall costs of the project is increased by 2000 kr. The project plan is then given as shown in Figure 11.

Figure 11: Project network of dependencies with Time-Cost computation

It is noted that both the sequence of task A, C and E as well as the sequence of task B and D now defines the new critical path. It is further seen that the length of the project is reduced by two days to have a total duration of 38 days, as wanted.

Discussion of limitations and the current state of the art

According to Professor of project management Graham M. Winch, the Critical Path Method is highly recommended by both researchers as well as leading specialists in project management. Especially in its PERT application where probabilistic methods are used to determine the time durations. Even though, many projects do not go beyond the use of bar charts in its planning . The reason for this is explained in the limitations of the method as well as organisational problems in the implementation.

Requires extensive computer power

First of all, for large projects there will be thousands of tasks and dependency networks to control. Without any software help this analysis requires a lot of resources and can be difficult to control. In addition, a project almost never tends to follow the same schedule all the way through the project duration. Changes due to uncertainty and unforeseen events always occur and updates to the plan are required. Before the 1990s the computer power was not cheap enough to have on site and it was therefore difficult to use the method as an everyday tool by the planners. The method tended to be, as Professor Winch explain it, a “historical oriented control tool, rather than a future-oriented management tool” . What he means by this is that since the method required too many resources to be updated it tended to be used to control how far behind the schedule the project was, rather than using the method as it was intended to, by always managing the optimal plan given the circumstances. However, computers are now an everyday tool, and as it has been illustrated in this article, the software used for the analyses are easily managed, so those limitations are likely to disappear.

The problem with time estimates

Another important problem follows from the tender phase of the construction projects. The tender phase is usually so fast that the project managers don’t have time to analyse and develop a proper construction plan. Since the master plan is developed highly based on the tender plan, the planned task durations are therefore rather guesses then based on an actual analysis. As mentioned, one of the most important assumptions regarding the method is that the method assumes that the task durations are known very precisely. Imprecise time estimates make the whole method useless. Nevertheless, a change in the construction industry is observed and the project managers tend to have more time to plan the projects . In addition to the uncertainty of the time estimates, the construction industry is bounded by contracts and penalties. The people in charge of a task are usually held responsible if the time schedule does not hold. The risk of delaying the time schedule therefore incurs to design for worst case scenarios. This means that a lot of time buffers are included in the time estimates. This is of course on the safe side, but it limits the whole concept of the method because the analysis can’t optimise the project plan if padding is included in every task. The method is only as good as the time estimates.

An additional problem connected to time buffers is explained by Parkinson’s law which states that “the amount of work rises to fill the time available to complete it” . This means if you have more time to finish a task then you will also use the time. Since it’s the same amount of work that should be done, the effectiveness is reduced by including time buffers. A solution to overcome the two issues could be either to build up a huge database of required duration to do a given task through detailed work studies, or alternatively change the culture to allow delays without the risk of penalties. By removing the time buffers on local tasks, the project managers gain a larger control of the project. The project manager can then include strategic project buffers to protect the critical path.

The method does not account for resources and allocation of resources

An important limitation with the method is also that it does not account for resources and allocation of resources . Standard Critical Path Methods assumes that resources are unlimited. This means that for instance a worker can be expected to work on two different tasks at the same time. However, there can be situations where resources can be shared. This could be a crane that is excepted to do more tasks at the same time. If the crane is not effectively used the entire time, then it can be shared with other tasks at the same time as other tasks uses the crane. A task needs space to be executed. The Critical Path Method does not take spatial analyses into account. If the project manager estimates that shared resources and sufficiently space might be a problem to the project, other methods can be used to support the Critical Path Method. The Critical Chain Method address the problem with resources. It computes the longest resource-constrained path in the same way as the Critical Path Method. So, the method is actually a development of the Critical Path Method. The space problem can be analysed by use of the Critical Space Method. It addresses the problem similarly as the Critical Chain Method by considering available space as a resource.

Conclusion

The aim of this article has been to analyse the Critical Path Method to find the advantages as well as the limitations of the method. The main benefit about the Critical Path Method is that it identifies all the dependencies and interactions between the tasks and point out the essential tasks that drive the project timeline. Thus, the project manager can make a better planning by knowing which tasks to pay special attention to. Furthermore, the method makes it possible to decide which tasks that can be delayed and how much without impacting the project schedule. The method has some historic oriented organisational problems in the implementation which defiantly has affected the use of the method. However, the development of software to speed up the analysis has only strengthened the method. The method is highly based on time estimates and the most important limitation with the method is the uncertainty of the task durations. The article concludes that even though probabilistic methods are used, it is recommended to research in work studies to get more reliable task durations. In addition, the article recommends removing the tasks buffers by introducing a no blame culture. The article further points out that the limitations of the method regarding resources and space can be handled by other methods, if the project manager estimates that they might be a problem to the project.

See also the related articles

• Gantt Chart in Project Management
• Last Planner System as a project management tool
• The Critical Chain Method
• The Last Planner System in Construction Projects
• Application of Dependency Structure Matrix in Time Scheduling
• 4D-Planning in Construction Management
• Comparison of Schedule Managing Methods

Annotated Bibliography

Fondahl, John W. (1962), Non-Computer Approach to the Critical Path Method for the Construction Industry, Stanford University, Available at https://www.google.dk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0ahUKEwj1i9XcwrHUAhUCAZoKHULODKcQFgglMAA&url=https%3A%2F%2Fwww.mosaicprojects.com.au%2FPDF%2FJohn_W_Fondahl.pdf&usg=AFQjCNEeXEGpFYJMm3DCkRAStzaomZxf9Q&sig2=HUNuv7BsxK1fL3QdLUQkWw (Visited on 18/06/2007)

The book gives a detailed explanation of the Critical Path Method for the Construction Industry. The approach is an application without any computer assistance so the book really goes into details with the method done by hand. The book is written in 1962 so it also serves as a historical approach of how the method was around the time of its development in the late 1950s.

Weber, Sandra C. (2005), Scheduling Construction Projects: Principles and Practices, Prentice Hall.

This book explains a number of different concepts regarding scheduling plaining in construction projects. The books describes the methods in a general matter with easily read text and with many illustrating examples.

Winch, Graham M. (2015), Managing Construction Projects, Wiley-Blackwell.

Managing Construction Projects gives a very good overview of the art of managing a project. It covers most of the subjects in management both in width and in depth. After each chapter, the book furthermore suggests additional readings to go in further depth width the subject.