Monte Carlo Simulation of Risk

Abstract

”To dare is to lose one’s footing momentarily. To not dare is to lose oneself” - Søren Kierkegaard

Staying dynamic is a means of survival in today’s modern society, thus the expression the burning platform. In order for companies to stay competitive and sustain their businesses, they have to either become cost leaders or product leaders i.e. innovative. In order to realize this, companies have to dive into new areas of business, explore new possibilities in terms of evolving their products and/or processes. During the process of exploring and maintaining dynamism, uncertainty is inevitable due to the respective volatile nature of the markets within which the diverse companies operate in. Companies can’t foresee the future, hence don’t know how their respective markets will react to their new ways of doing business, new products or on the other hand if they are resilient enough to sustain unexpected drawbacks when exploring new paths. Thus it can be concluded that risk is incorporated in the DNA of any project, program or portfolio management, therefore “Risk Management” is a necessity for companies to continuously embark when exploring new dimensions in order to mitigate risk and suppress their corresponding consequences. There are several ways in which risk management can be conducted. This article provides a profound description of how to conduct a quantitative risk assessment by means of utilizing Monte Carlo simulations. Risk is random since its uncertain thus Monte Carlo Simulations are utilized to simulate it by means of a probability distribution.

• not complete*

Risk

It is basically inevitable not to associate risk and uncertainty to any human activity although they can vary from activity to activity, depending on what’s at stake. In literature, risk in management has been defined as the probability (chance) of an event occurring, which could eventually result (uncertainty) into a negative impact (consequence) on a particular project in context thus risk is an expected loss over time.

Risk = Probability of risk occurring ×Impact of risk occurring

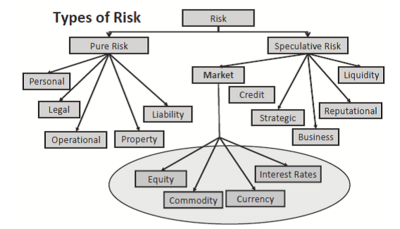
Risk can be categorized as either pure or speculative , as depicted in Figure 1.1 Regarding pure risk, there is no benefit or gain pertained to it, thus loss is the only possible outcome e.g. companies exposed to fraud or damage of assets etc. On the other hand, speculative risk can result into an uncertain degree of loss or gain e.g. a company can either gain or lose on investing in a new product, since there is a risk of market rejection. In this article emphasis is laid on speculative risk.

Figure 1.1: Categorize of risk.

.

Risk Management

When dealing with project, program or portfolio management it is crucial to understand that a lot of uncertainties (risks) are pertained to them, since their eventual benefits are projected into the future (vision/goal). These uncertainties occur randomly within the lifecycle of the different categorize of management, thus eventually resulting into delays, budget overruns and eventually terminations, if not managed hence the importance of risk management.

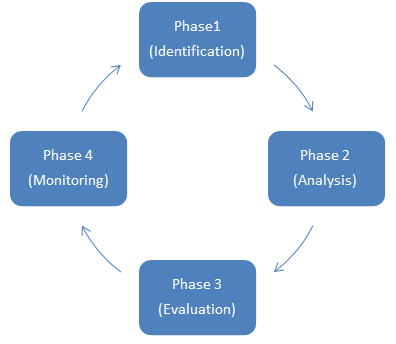
According to ISO 31000 risk management is the coordination of activities to direct and control an organization with regards to risk. In literature risk management can be decomposed into four continuous phases i.e. risk - Identification, Analysis, Evaluation and Monitoring as depicted in Figure 2.1 and elaborated below. Before embarking on a risk management course, it is crucial to commence with a risk management plan. Risk management planning is the structuring and detailing of how the risk management process is going to be conducted throughout the lifecycle of a project . Subjects such as methodology, practices, roles and responsibilities, sequence and timing of activities are pertained to risk management planning .

Figure2.1:Phases of risk management

.

• Phase 1: Risk Identification :

This phase involves the pinpointing of potential risks that might eventually affect a particular project in context and their causes. It is usually conducted by domain experts by means of brain storming

• Phase 2: Risk Analysis:

This phase involves the comprehension of the nature of the initially identified risks and an estimation of their consequences , since risk have different severity degrees. Risk analysis can be sub divided into qualitative and quantitative risk analysis. Both approaches can be utilized in one project but in order to conduct a quantitative analysis, estimates from the qualitative analysis is needed. On the other hand risk analysts can chose to stop with a qualitative risk analysis if the project is not too big.

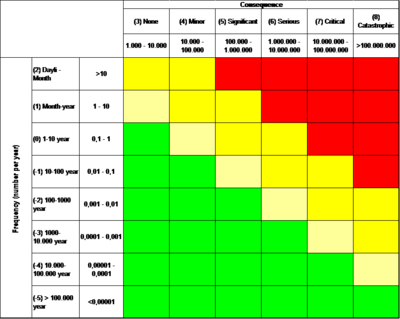
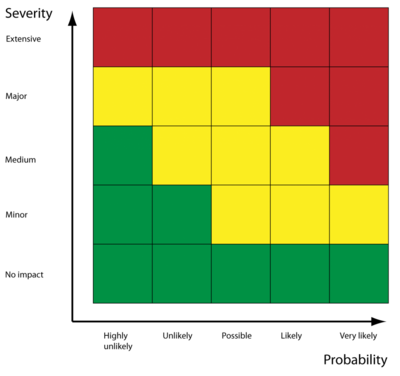
Qualitative risk analysis:In a qualitative risk analysis descriptions and estimates (mostly in monetary terms) of the different consequences pertained to the different risks, estimates of their occurrence (frequency) and means by which they can be mitigated are listed. Furthermore the different risks are prioritized, which provides the foundation for the evaluation phase. Figure 2.2 shows an overview of how the different risks can be prioritized according to severity.

Figure2.2:Risk Matrix for prioritizing risks bases on frequency and consequences in monetary terms

.

Quantitative risk analysis:Quantitative risk analysis is a process of quantifying various impacts of identified risks imposed on a specific project in context, by means of using their estimates from the qualitative analysis. The quantification process is conducted by allocating different probability distributions to respective risks and thus simulating hypothetical events (scenarios) of the identified risks

• Phase 3: Evaluation:

This phase involves the evaluation of the different risks by means of comparison in terms of severities and frequencies thus the establishment of tolerability levels. Organizations can in this phase chose to accept, try to avoid, transfer the risks or terminate the project if the risks are too high.

• Phase 4:Risk Monitoring and Control :

This phase involves the continuous monitoring, supervising and controlling of the different identified risks . New risks that were not initially identified could also surface along a projects lifecycle, thus the necessity of continuously reassessing and revaluating risks. Figure 2.3 depicts a more detailed process of Risk management.

Figure 2.3: Different processes pertained in the four phases of risk management

.

Monte Carlo Simulation

In order to elaborate on what a Monte Carlo simulation is, the following terms must be understood in order to facilitate the comprehension of the concept of Monte Carlo simulation:

• Random variable (Stochastic variable):

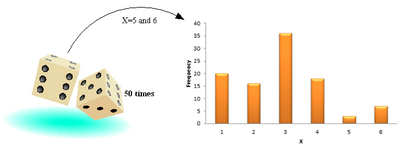
A variable is any defined characteristic that is subjected to variation either due to natural and /or imposed factors e.g. height, age, temperature etc. A random variable on the other hand is any function that allocates a numerical value to each possible outcome i.e. a measurement or a count of a variable (characteristic) that varies randomly according to a certain pattern. Random variables can be categorized into two categories depending on the type of outcome from a certain pattern; Discrete or continuous. Discrete random variables are outcomes of random variables that are either finite or countably infinite, whereas if the set of possible outcomes of a random variable is an interval, then it is continuous . E.g. when throwing two deices fifty times simultaneously as depicted in Figure 3.1, a player can’t predict what the outcome will be due to uncertainty, therefore when the outcome results into 5 and 6, the values are termed as random variables.

Figure 3.1: Frequency table of dice throwing

.

• Probability distribution:

Probability is the chance of something in particular occurring e.g. when playing Russian roulette with a six chamber revolver loaded with one bullet, the probability of pulling the trigger thus igniting the bullet is P(X=bullet)=1/6. A distribution on the other hand is the listing of viable/intervals of values of a characteristic (variable). A probability distribution can thus be defined as the probability structure of a random variable i.e. in other words the probability (chance) of a random variable taking on a value within a certain set of possible outcomes, whereas each of those outcomes have a certain probability of occurring. It should be noted that when dealing with discrete random variables, the probability distribution of the variable is referred to as the probability mass function, and on the other hand probability density function when dealing with continuous random variables .

Thus a Monte Carlo simulation can be defined as a quantitative approach of quantifying risks, by means of utilizing a probability distribution (Tysiak & Sereseanu, 2010). This is because risk is random and uncertain; therefore it can be classified as a random variable i.e. something that occurs by chance. Hence a Monte Carlo simulation of a particular project in context selects random variables from a given probability distribution of risk that is modeled by means of estimates. This is in order to figure out which risk has the highest certainty of occurring based on the probability distribution allocated to it. Furthermore, a Monte Carlo simulation enables the correlation of various risk factors, by means of incorporating a probability distribution for each conditional relationship (McCabe, 2003), (Hargreaves, 2011). This thus facilitates the process of comprehending and assessing the various impacts of risks associated to a certain project and the pinpointing of ways in which they relate to each other.