Financial Portfolio Optimization Methods

Quantification of Financial Risk TO BE EDITED,ADD BIBLIOGRAPHY AND FIGURES

In today's globalized market, financial risk and treatment of it that has gained great importance, especially after the Financial crisis of 2008, where factors which may affect the fragile global economy proved to be thousands and often unconnected to each other. Nations fail to pay their debts and giants of the finance industry bailed out . These financial institutions have developed various quantitative methods which can give a prediction of this risk level in financial portfolios. A financial portfolio is considered the summary of investments owned by an investor ( company or individual ). The first step for the quantitative measurement of risk in portfolios was made by Harry Markowitz in 1952 , with the development of the mean-variance model as risk measurement, which shows interest until today and it is used by investors. Thereafter, various other methods were developed, focusing on alternative risk measures that could lead to linearization of the portfolio optimization problem .

Models of Optimization

Background

The term efficient portfolios was developed in the 1950's by Harry Markowitz , . An efficient portfolio is one that at given level of risk provides the greatest return and at given performance holds the less amount of risk. According to this definition, an investor will choose from a set of possible portfolios, the portfolio which:

1. offers the maximum expected return for different levels of risk
2. offers the lowest risk for different levels of expected return.

Those portfolios that meet the before-mentioned requirements are considered as effective ones. Figure 2.1 shows an example where all the possible portfolios which are formed based on the expected return and risk relations. The set of efficient portfolios has the form of a parabola in between the axes of the expected return (vertical axis) and the level of risk (horizontal axis). Points A, B, C, D, E, F, show some of the possible portfolios. Of all the available portfolios, the most efficient ones are those found in "northwestern" part of the curve of efficient portfolios between A and F. All other portfolios are regarded as ineffective. For example, the A portfolio excels E because it offers the same performance with less risk. Similarly the C portfolio excels D because it offers more return at the same risk level.

(eikona tou efficient frontier)

Assumptions

A series of assumptions regarding the market and investors were made in order to quantify risk

• Investors are "reasonable" and behave in such a way to maximize their benefits according to the available capital.
• Investors have free access to a fair and accurate information concerning risk and expected returns.
• Markets are efficient and absorb information quickly and perfect.
• Investors avoid risk through the effort to maximize the profit and minimize the danger of investments.
• Investors base their decisions in accordance with the expected performance and a mathematically defined risk measure.
• Investors prefer higher returns than lower ones at a given risk levels.

Mean Variance Model

This model of optimization financial portfolios was the beginning of Modern Portfolio Theory and was the cornerstone for the study of risk in securities. It is still used because of its simplicity and its greater degree of physical understanding of the mathematical aspects, however its non-linear nature raises the complexity of solution in order to find the best portfolio compared to models that are linear and will be further discussed below. In the case of this model it is assumed that there are 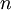$n$ bonds. 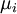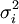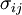Each bond $i$ has expected return $\mu_{i}$, the variation of performance is denoted as $\sigma_{i}^2$, and $\sigma_{ij}$ is the co-variance of returns in relation to another security 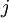$j$. 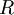If $R$ is the desired performance of the portfolio then:

$\begin{align} \min \quad & \sum\limits_{i=1}^n \sum\limits_{j=1}^n \sigma_{ij} w_{i} w_{j}, \\ \text{s.t} & \sum\limits_{i=1}^n w_{i} \mu_{i}\geq R ,\\ & \sum\limits_{i=1}^n w_{i} = 1,\\ & w_{i} \geq 0 , i= 1,2,3...n \end{align}$

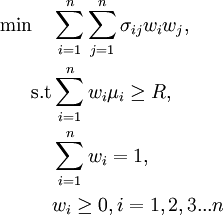
The term 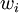$w_{i}$ represents the percentage of the capital that will be invested in each bond. This is a quadratic programming problem, and hence the solvability puzzled the financial industry for many years. Today, however, the available computational tools enable the solution of the above quadratic program even for large-scale data .

Mean Semi-Variance Model

An alternative to the problem of portfolio optimization using mean variance is to use the term of the average semi-variance, a proposal made again by Markowitz , . Because an investor is more concerned about minimizing under-performance instead of over-performance, the semi-variance was considered as a more appropriate measure of the risk variance .The difference is that semi-variance measures only downward deflection, not both negative and positive deflections as described in Mean Variance model . This model seeks to identify optimal portfolios considering the expected outcomes of each security and its the semi-variance such as discussed above . The efficient portfolios of the solution of this problem have little semi-variance for a given expected return, and maximum expected return for a given semi-variance. The set of all efficient portfolios form the efficient frontier in returns / semi-variance graph. The linear minimization problem formulized by the above is:

$\begin{align} \min \quad & \sum\limits_{t=1}^T z_{t}^{2}, \\ \text{s.t} & \sum\limits_{i=1}^n w_{i} = 1 \\ & \frac{1}{\sqrt{T}}\sum_{i=1}^{n}(r_{ti}-\mu_i)-d_t+z_t=0,\quad t=1,2,\ldots,T, \\ & \sum\limits_{i=1}^n w_{i} \mu_{i} \geq R, \\ & w_{i} \geq 0 , i= 1,2,3...n \end{align}$

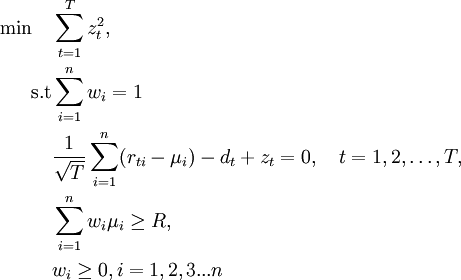
The above modeling led to the first form of utilization of risk of deterioration as a risk measure, which although it is computationally difficult in cases where further restrictions are added , it is a quite popular method .

CVaR Model

The Conditional Value at Risk, (CVAR) is an extension of the term value at risk (VaR) , in order to create a better estimation of losses in extreme adverse conditions and to address certain theoretical problems of the value at risk . For continuous distributions, CVAR is defined as the expected loss in those cases where the loss of an investment position exceed the corresponding VaR. However, for general loss distributions, including discrete distributions, the CVAR is defined as the weighted average of the VaR and losses that strictly exceed VaR . For general distributions, the CVAR, has more attractive properties from VaR[καινουριο paper CVaR]. CVaR is subadditive and convex . In addition, the CVAR has all the essential qualities of a reasonable risk measure, which does not happen in the occasion of VaR, according to Artzner , . Although CVaR is not fully accepted in the financial industry, it is gaining ground in the insurance sector [12]. Mathematical formulation of CVaR is :

$\begin{align} \min \quad &\eta + \frac{1}{T\beta} \sum\limits_{t=1}^T d_{t},\\ \text{s.t} &\sum\limits_{i=1}^n w_{i} = 1 \\ &\sum\limits_{i=1}^n w_{i} \mu_{i} \geq R,\\ & n+\sum_{i=1}^{n}{r_{ti}w_i}+d_{t}\ge 0,\\ &d_{t} \ge 0 \qquad t=1, 2, \ldots, T\\ &w_{i} \geq 0 , i= 1,2,3...n \end{align}$

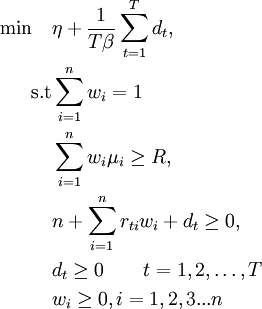
Optimization of CVaR minimizes VaR, since 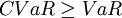$CVaR \geq VaR$ .Furthermore another advantage of CVaR against simple VaR is that it can be optimized by linear programming methods and thus creating optimal portfolio can become a process of solving a linear problem which is relatively simple to understand and easy to use as well as its implementation is undemanding .

Mean Absolute Deviation Model

The difficulties of solving the model of Markowitz and variants led Konno and Yamazaki in 1988 to present a model consisting exclusively of linear constraints , which utilizes as a measure of risk the mean absolute deviation (MAD) . Mean absolute deviation is defined as the average of the absolute deviation from the mean of the data. So the following formula was proposed as risk measure:

$\begin{align} MAD_{i} = \frac{1}{T} \sum\limits_{i=1}^n \left\vert r_{it}-\mu_{i} \right\vert \end{align}$

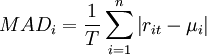
Extending this risk measure to financial portfolios it is observable that because of the absolute nature of risk measurement, the generated problem can not be linear. But it can easily be transformed to one by adding a further variable. So the problem presented for solution is the following:

$\begin{align} \min \quad & \sum\limits_{t=1}^T y_{t} , \\ \text{s.t} & \sum\limits_{i=1}^n w_{i}[r_{ti}-\mu_{i}]+y_{t} \geq 0 \\ & \sum\limits_{i=1}^n w_{i}[r_{it}-\mu_{i}]-y_{t} \geq 0 \\ & \sum\limits_{i=1}^n w_{i} \mu_{i} \geq R ,\\ & \sum\limits_{i=1}^n w_{i} = 1 \\ & y_{t} \geq 0 \quad t=1,2,3....T \\ & w_{i} \geq 0 , i= 1,2,3...n \end{align}$

The above modeling helps in examination of a larger number of securities due to the ease in solving a problem of linear constraints as well as the addition of constraints that make it realistic becomes more computationally viable .

Additional Constraints

In real situations where investors desire portfolios that meet different realistic features like minimum lots of transactions and transaction costs, solvability of linear models is a critical aspect. Even if the solution of quadratic models like Mean Variance and Semi-Variance has been treated for restrictions in the total number of shares and minimum transactions lots , the computational challenge to solve the big and realistic portfolio problems justifies the long tradition in literature of mixed integer programming for portfolio selection with pragmatic characteristics . The models extend the basic portfolio optimization models and result to increased complexity and difficulty of solution. However, the analyzes carried out are closer to reality and the parameters can be adjusted depending on the stock market and investor requirements. Such restrictions can be:

• Restriction in total number of shares. The investor chooses the maximum number of shares they want to invest.
• Limitation of minimum trading lots. The investor virtually round the percentages invested, due to limitations of the financial market.
• Limitations of transaction costs. Certain financial markets have set different transaction fee for different amounts of investments, parameter that the investor must consider at each update an existing portfolio.

Transaction Costs

Portfolio optimization, taking into account the cost of transactions aims to minimize the sum of transaction costs and risk. Once a subset of the securities is selected by the investor, the costs are easily calculated . The goal of this model is to determine the subset of the portfolio which minimizes these costs . Intuitively, if a transaction cost for a particular asset is too large, it may not be a positive change to include that security in portfolios. Alternatively, if the transaction price is small enough, it may be good to make the change even if this adds some transaction costs in to the whole investment. This problem may ,depending on the formulation, lead to complex quadratic problems with great amount of solving difficulties. It will be presented a linear edition of this problem as it is clearly easier to solve and realistic in terms of real-time portfolio management , . Modeling is based on the designation of transaction costs through a piecewise linear function, as it is assumed that the cost changes to specific threshold points of the trading volume, as shown in Figure !!. Implementation is expressed mathematically :

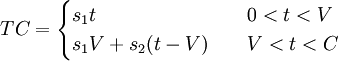
$\begin{align} TC = \begin{cas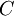es} s_{1} t & \quad 0 <t<V \\ s_{1} V+ s_{2}(t-V) & \quad V<t<C \\ \end{cases} \\ \end{align}$

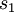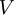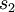as $C$ denotes the capital available for investment, $s_{1}$ is the cost for transactions that their value do not exceed a predetermined threshold $V$ and $s_{2 }$ is cost for higher amount of transactions (transaction costs are considered as a percentage of the transaction value). So the overall modeling of problems with transaction costs are:

$\begin{align} \min \quad & Z_{TC}=f_{obj}+\sum\limits_{i=1}^n(s_{1i}c_{1i}+s_{2i}c_{2i}),\\ \text{s.t} \quad &z_{i}=c_{1i}+c_{2i}\\ \quad &z_{i}\ge w_i - w_{0i},\\ \quad &z_{i}\ge w_{0i} - w_i,\\ \quad &w\in \mathcal{A} \\ \quad & 0 \leq c_{1i} \le V\\ \quad & 0 \leq c_{2i}\le C-V \end{align}$

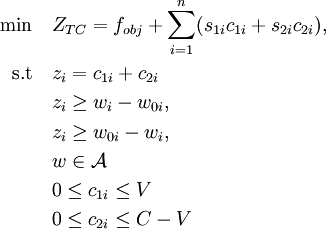
where 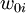$w_{0i}$ is the participation of share $i$ in a portfolio already possessed by the investor, as 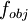$f_{obj}$ is symbolized the objective function of one of the major portfolio optimization models discussed above and 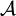$\mathcal{A}$ is the corresponding set of feasible solutions. The above modeling solves efficiently in terms of time the problem of transaction costs.

Transaction roundlots

In any stock market transactions take place in predetermined units (pieces) of each security. Such restrictions are common transactions requirements which means that investing in a security should be expressed as a multiple of a predetermined unit of transaction . The monetary value of each transaction unit is expressed as a percentage of the value of a portfolio [16] so that the composition of the portfolio ( percentage of participation of securities) shall be defined based on these percentages. Moreover limitation of budget becomes "flexible" by the introduction of deviation variables. 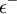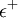These variables are denoted as $\epsilon^{-}$ and $\epsilon^{+}$ , which are minimized in order to limit the budget impbalances as little as possible at the optimal solution . To achieve this, the deviation variables should have very small values .

Disadvantages

In literature there has been reported that many of these assumptions do not seem realistic. Assumption of "reasonable investors" often seem to fall short as they generally prefer portfolios different from those resulting from analyzes . Moreover, the grade of complexity becomes greater as the problem grows and its solution becomes extremely difficult or even impossible. Finally, the assumptions mentioned do not take into account the uniqueness of each investor and consider everyone as a unified body, ignoring the behavior that each of them may present. So the difference of institutional and non-institutional investors can lead to values much higher than actual, due to herd behavior in the second category of investors, leading to systematic overvaluation of stock prices . This kind of disadvantages seem to gave birth to various approaches in the problem of portfolio optimization. Fuzzy handling of the problem , seem to solve various of the issues made due to the assumptions such as the nonuniform character of the information among the investors,pigi . Moreover multi-criteria analysis haw been implemented in order cope with the investor’s personal attitude towards risk and specific objectives he/she may have .

Other Implementations

These basic models of financial portfolio optimization, that basically derive from the Modern Portofolio Theory, seem to have the eligibility to be implemented in more than one applications. The ability to choose the most appropriate set of projects and allocate the amount of in the most efficient way is a desired practical aspect of this mathematical theory. The utilization of MPT in water resource portfolios enabled the researchers to reduce drought problems . Moreover, the same principles were implemented on intervening against the high nutrient loads at the river catchments and had as a main result better budget allocation on environmental investment decision processes . MPT is a valuable set of tools for every investor that works his way through uncertainty and vastness of the problem of budget allocation.