Epistemic vs. Aleatory uncertainty
Developed by Panagiotis Vounatsos
Contents |
Abstract
Uncertainty is embedded in many aspects of project, program and portfolio management. It is present in decision making for project integration and complexity, scope management, schedule management, cost management, and risk management as this is mentioned in PMI standards, and in risk management given in AXELOS standards.
Uncertainty derives from not knowing for sure if a statement is true or false. More specifically, it is the absence of information and if put more scientifically, it is the difference between the amount of information required to perform a task and the amount of information already possessed[1]. Uncertainty is considered crucial to be identified and mitigated as it can contribute to severe consequences to a project, program or portfolio. Depending on the level of the uncertainty and the consequence it may result in jeopardizing the outcome of an action or even of the whole project. It is worth mentioning that uncertainty is not only a part of project management but also a part of the technical implementation of a project.
Uncertainty can be divided in two types which are epistemic and aleatory uncertainty[2]. Epistemic uncertainty derives from the lack of knowledge of a parameter, phenomenon or process, while aleatory uncertainty refers to uncertainty caused by probabilistic variations in a random event [3]. Each of these two different types of uncertainty has its own unique set of characteristics that separate it from the other and can be quantified through different methods. Some of these methods include simulation, statistical analysis, and measurements[4]. The capability to quantify uncertainty and the potential impact in decision context is critical.
What is Uncertainty
Different definitions have been given for uncertainty in project management, but their common denominator is “not knowing for sure”. There is information that is known to be true and other known to be false, but for a large portion of information there is no knowledge whether they are true or false, and therefore they are mentioned as uncertain[1]. According to Lindley[5], uncertainty can be considered as subjective between individuals, because the set of information obtained from an individual can differ from another. Two facts that apply are: a) the degree of uncertainty between individuals may differ, meaning that one person may think that an event is more likely to happen that another person, b) The number of uncertain information is vastly greater than the number of information each individual is sure that is true or false[5]. These two facts deeply affect decision making, considering that uncertainty creates the contingency for the occurrence of risky events which lead to potential damage or loss.
Epistemic vs. Aleatory uncertainty
Uncertainty is categorized into two types: epistemic (also known as systematic or reducible uncertainty) and aleatory (also known as statistical or irreducible uncertainty)[6].
- Epistemic Uncertainty derives its name from the Greek word “επιστήμη” (episteme) which can be roughly translated as knowledge. Therefore, epistemic uncertainty is presumed to derive from the lack of knowledge of information regarding the phenomena that dictate how a system should behave, ultimately affecting the outcome of an event. [2][6].
- Aleatory Uncertainty derives its name from the Latin word “alea” which is translated as “the roll of the dice”. Therefore, aleatory uncertainty can be defined as the internal randomness of phenomena [2].
Key features of Epistemic and Aleatory Uncertainty
Key features characterizing pure epistemic and pure aleatory uncertainty are distinguished according to judgement and decision making.
Representation
Epistemic uncertainty targets single cases (or statements), while aleatory uncertainty focuses on a range of possible outcomes that can derive from the repetition of an event. Robinson et al. (2006) as cited in Fox and Ülkümen (2011)[7], carried out an experiment asking children to predict the color of a building block drawn from a bag containing only two colors. When the children were asked before the experimenter drew a block, they chose both colors as a possible outcome. When asked after the experimenter drew and before revealing a block, they usually made one choice based on their best guess. This experiment suggests that when the likelihood of a single or a group of events is calculated, this may prime epistemic and aleatory representation, respectively.
Focus of Prediction
Judgement of purely epistemic uncertainty generally leads to the evaluation of events that will be true or false. In contrast, purely aleatory uncertainty leads to the evaluation of the trend of each event on continuous unit interval. According to that, small changes in evidence strength greatly affect pure epistemic events leading them towards extreme values (true or false), compared to judgement of events that include aleatory uncertainty[7]. For example, if there is high confidence that a project is slightly costlier than another, then the probability that the first project is more expensive than the second one is judged as 1. However, if there is confidence that a project is marginally more innovative than another, then the probability that it will create more value is less than 1, e.g. 70%.
Probability interpretation
The interpretation of pure aleatory uncertainty is carried out as an extensional measure of relative frequency, while the interpretation of pure epistemic uncertainty is conducted as an intentional measure of confidence. In this manner, using relative frequency may trigger more aleatory thinking than drawing out probability numbers. Several studies indicate that erroneously judging a combined probable and improbable event as more likely to happen than an improbable event alone, occurs less often when judging relative frequencies than single event probabilities[7].
Attribution of uncertainty
Unpredictable outcomes that are treated as random (e.g. the result from the roll of a dice) relate to aleatory uncertainty. Events or outcomes that occur due to missing information/expertise (e.g. lack of knowledge) or inefficiency of an aleatory uncertainty model (e.g. whether the assumptions made for forecasting energy demand are valid) are associated with epistemic uncertainty. Behavior analysis shows that decision makers prefer choosing events with known aleatory uncertainty rather than events with high epistemic uncertainty. Ellsberg’s paradox is a widely known experiment that illustrates decision making under epistemic and aleatory uncertainty[7].
Information search
Epistemic uncertainty is attributed to missing information or expertise. Therefore, it can be reduced by searching for knowledge that will allow predicting its outcome with greater accuracy. On the contrary, the determined relative frequency of possible outcomes for aleatory uncertainty cannot be further reduced[7]. For example, a program manager must choose between projects which may or may not contribute to the program's benefits and outputs. An epistemic mindset would alter the choices exploring the combination of projects (size, type, complexity) that govern the sequence for success contributing to outputs. An aleatory mindset would find which combination of project size, type and complexity is more often successful and run only projects of these characteristics.
Linguistic Markers
Hutchins as cited in Fox and Ülkümen (2011)[7] has identified that natural languages reflect the intuitive distinguish of cognitive concepts from individuals. Epistemic and aleatory uncertainty incorporation in natural language was anticipated and empirically validated (Teigen and Fox, Üklümen and Malle as cited in Fox and Ülkümen (2011)[7]). For example, phrases “I am 70% sure that…” and “I think there is a 75% change that…” express epistemic and aleatory uncertainty respectively.
The following table (Table 1) summarizes the key features of pure aleatory and epistemic uncertainty.
| Epistemic | Aleatory | |
| Representation | Single case | Class of possible outcomes |
| Focus of Prediction | Binary truth value | Event propensity |
| Probability Interpretation | Confidence | Relative frequency |
| Attribution of Uncertainty | Inadequate knowledge | Stochastic behaviour |
| Information Search | Patterns, causes, facts | Relative frequencies |
| Linguistic Marker | “Sure”, “Confident” | “Chance”, “Probability” |
Causes of epistemic and aleatory uncertainty
Different causes of uncertainty can be recognized as given by Armacosta and Pet-Edwards, and Zimmermann cited in Zio and Pedroni [6].
- Lack of information (or knowledge). Lack of information can be categorized as lack of a precise probabilistic value (quantitative nature) or as lack of knowledge in mathematically analyzing the known probabilistic values (qualitative nature) of an event. Lack of knowledge also affects the detail of the mathematical method used to analyze the probabilistic values of an event. Approximation is the situation when there is not enough information or reason to describe the event in a high level of detail. An example is when a project manager takes into consideration several parameters to calculate the project’s cost. To what extent is it needed to calculate the value of few low-cost equipment down to two decimals, if the total budgeted cost exceeds several million units?
- Abundance of information (or knowledge). Humans are incapable of simultaneously assimilating and elaborating many pieces of information, and that leads to uncertainty from abundance of information. When there is overwhelming information, attention is only given to pieces of information considered as the most important, while others are neglected. For example, this uncertainty occurs when there are different models for the analyst to choose among, in order to analyze an event.
- Conflicting nature of pieces of information/data. This uncertainty occurs when some pieces of information give contradicting knowledge, and it cannot be reduced by increasing the amount of information. This conflict can derive from the facts that information is a) affected by unidentified from the analyst errors, or b) irrelevant to the event analyzed, or the model used to analyze the system is incorrect.
- Measurement errors. Uncertainty is created by errors in the measurement of a physical quantity and occurs either from an error of the measurement taker or from insufficient accuracy of the used instrument.
- Linguistic ambiguity. All communication forms can be structured in a way that can be differently interpreted depending on the analysis context. This cause of uncertainty is included in the “lack of information” category because it can be reduced by clarifying the context.
- Subjectivity of analyst opinions. This uncertainty emanates from the subjective interpretation of information by the analyst, depending on their personal experience, competence, and cultural background. This uncertainty can be reduced by taking into consideration the opinions of several different experts.
Uncertainty in Management
Project Management
Project management deals with uncertainty on several different levels.
- Integration and complexity. Uncertainty within an organization or its environment leads to the increase of a projects’ complexity. [8]. E.g. Team formation may prove difficult when there is uncertainty on interpersonal relationship of team members.
- Scope definition. High uncertainty may lead to initially misunderstand the project’s scope or leads the scope to evolve during the project [8]. E.g. What work steps are needed if the final product is not clearly determined and may change in the duration of the project?
- Scheduling. High uncertainty in the current competitive marketplace creates the necessity to effectively adopt development practices, including more effective project scheduling methods[8]. E.g. Delay in project tasks that are not in the critical chain may be tackled by proper rescheduling, in order not to delay project completion.
- Cost management. High degree of uncertainty leads to frequent changes and this fact does not permit detailed cost calculations. It rather calls for lightweight estimation methods providing an easily adjustable high-level forecast[8]. E.g. How many manhours should be calculated if there is uncertainty for the extend of the task to be carried out?
In order to reduce any impact of the risk associated with the uncertainty, Project Risk Management addresses risk (an effect of uncertainty) in individual objectives and in the overall of the project[8].
Program Management
At the beginning of the program where the outcomes are not yet clear, uncertainty is considered to be very high. Two factors that contribute to high uncertainty regarding the outputs, benefits, and outcomes of the program’s work are the internal organizational environment and the changes in the external environment. Within the organization’s environment, programs have higher uncertainty compared to individual projects. Programs can tackle some uncertainty for their goals, budget, and timeline by changing the direction and implementation of projects. However, this practice creates more uncertainty regarding the programs’ final direction and outcomes. For example, the program management style needs to be selected to properly identify and tackle the uncertainty created by the continuously progressing and altering the scope and content of the program. Uncertainty is also added by the fact that some of the projects may not actually create added value to the program’s outcomes and benefits, even though their completion was successful[9].
Portfolio Management
In portfolio management, uncertainty is a factor that is incorporated in risk taken in order to maximize the portfolio’s value. Balancing the risk of different actions is challenging, due to the complex nature of portfolios and the inherent uncertainty associated with risk. A source of uncertainty is imperfect or incomplete information, and the higher the uncertainty the more important risk attitude perception becomes. Uncertainty can also derive from not minimizing threats but rather embracing them in anticipation of high rewards. An example is investing in a new promising, yet unproven technology in order to be “the first in the market”, expecting highly profitable sales. In the previous case, uncertainty lies in the decision to trust a technology while at the same time accepting the possibility of the technology failing. Furthermore, uncertainty can originate from within the organization's internal environment based on different decision making actions, e.g. whether a management practice chosen is the appropriate one or whether depending on highly specialized external assistance should be implemented. Compared to projects and programs, uncertainty is higher at the portfolio level, because of the impact of uncontrolled variables on the portfolio. For that reason, when uncertainty is growing, solutions are based on the perception to fill in imperfect or incomplete information[10].
Project, program and portfolio management may seem to have epistemic uncertainty in different aspects, but decision making can be made by following the same methodologies. Depending on the level of knowledge of the decision maker for the system, the uncertainties can be aleatory, epistemic or a combination of these two.
Epistemic uncertainty, value uncertainty, and decision making
Decision making under epistemic uncertainty is categorized into four types [11], depending on the level of epistemic uncertainty and the uncertainty of the gained value.
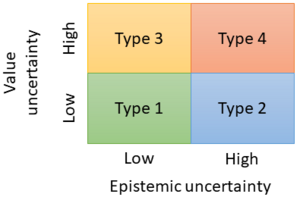
- Type 1 decision: I am sure what I want, and I know the odds. The decision maker has a lot of information regarding the precision of probability estimates, as well as clear personal preferences and values. Example: Consider a PC refurbishing company and a PC with two RAM memories. A decision needs to be taken regarding two available RAM. They can either be installed in the existing PC, checked if they are faulty and could create short-circuit, or thrown away. If the knowledge of the supplied quality is good, then the probability is known for the remaining RAM memories to be good. The epistemic uncertainty is low to non-existent and a PC with more RAM is far better than one with less or a burnt PC.
- Type 2 decision: I am sure what I want, but I do not know the odds. The decision maker has clear values and preferences, but the available information is poor regarding quality and quantity and is insufficient to represent uncertainty as a probability. Example: Consider that an organization wants to invest in new technology and can profit by being the first in the market. However, the technology is unproven and there is uncertainty in the organizational environment. In this case, the epistemic state is unknown as well as the magnitude and nature of the risks.
- Type 3 decision: I am not sure what I want, but I know the odds. The decision maker has poorly defined preferences and values. Furthermore, the information quantity and quality are good enough to calculate precise probabilities. Example: A subject considers investing all their money to a startup company in order to pursue an idea that will bring some good profit. After research, the subject identifies that startup companies have a high failure rate, and if this happens they end up bankrupt and in dept. The probability for such events is known to a reasonable precision through the existing corporate databases. This is a situation where the preference can be blurred and unclear due to lack of experience.
- Type 4 decision: I am not sure what I want, and I do not know the odds. In Type 4 decision neither the preferences/values nor the available information can be considered fixed or reliable. Example: A company has a social media platform. After several expensive marketing projects, the platform still has low market share, far lower than the minimum expectations. The estimation of the probabilities that the marketing project is going to be successful after some attempts, is becoming increasingly harder to make. That means that the epistemic state is unclear, and it deteriorates. This fact affects the preference (keep the social media platform running or not) and makes it increasingly unstable.
Despite the categorization of gained value and epistemic uncertainty into four types (Figure 1), the complete picture is more complex.
Quantification of uncertainty
Aleatory uncertainty quantification methods
For quantifying aleatory uncertainty, systematic probability and mature statistical tools are used. The most common representations of aleatory uncertainty are[12]:
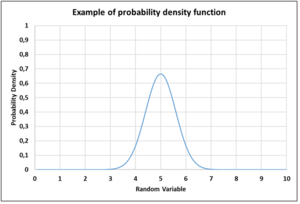
- Probability density function (graph example given in figure 2) is used to quantify the probability density at any point within the interval of a random variable.
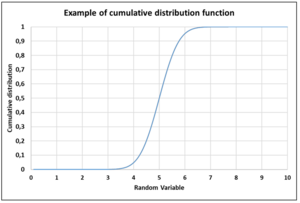
- Cumulative distribution function (graph example given in figure 3), gives the probability that a variable will be equal or less that a given value.
Epistemic uncertainty quantification methods
In literature, the most common methods of modeling epistemic uncertainty are the following.
- Bayesian probability is a method that appoints a frequency or probability of an event, based on an educated guess or a personal belief.
- Evidence theory, also known and as Dempster-Shafer theory or theory of belief functions. It is a generalized version of the Bayesian theory of subjective probability. The method bases the belief that an event is true on the probabilities of other hypotheses or events, which are related to the event under investigation [13].
- Interval analysis or probability boxes, assumes that the input variable is described by a range with lower and upper bound. This variable is subjected to interval mathematics that can result in providing all the possible values of the probability for the identified boundaries[13].
- Probability theory allows for better results than evidence theory because it represents uncertainty that includes a specification of more structure. The method can result in providing only the probability as a measure of chance [14].
- Possibility theory is a representation of uncertainty that allows a better structure compared to interval analysis. It provides a measure of the likelihood or subjective confidence for an event, for every state of the given event[14].
- Fuzzy set theory which can be extended to probability theory where membership functions are interpreted in possibility distributions [15].
- Generalized information theory which dictates that if uncertainty is adequately quantified, then the information (data or knowledge) that is gained from an action that leads to the reduction of uncertainty can be measured [16].
Limitations
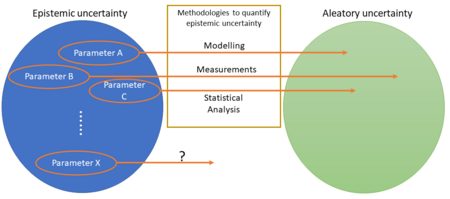
Uncertainty quantification is constrained by limitations. In some cases, uncertainty cannot be fully analyzed. Figure 4, is an example of the representation of the unknown parameters of an event (epistemic uncertainty), that after applying quantification methods are reduced to aleatory uncertainty representation. However, as mentioned in the causes of uncertainty there may be some parameters that the analyst still lacks the knowledge of how to transform them into aleatory. Therefore, the initial problem will still keep some epistemic uncertainty, and that fact can be considered as a limitation to fully identifying the underlying uncertainty.
Inability to quantify uncertainty due to:
- Lack of knowledge (we don’t know that something could affect our project)
- Total or partial lack of data (complete ignorance or uncertain knowledge of the extent that an event affects our project)
Limitations on quantification:
- Density function is calculated based on prediction, based on past data, model adequacy or expert opinion
- Past data may not describe accurately the future (unexpected event)
- The model used may not be adequate for forecasting
- Expert opinion may be biased due to education, knowledge or experience
- The chosen approaching method may not be optimal to describe a certain event/situation
- Approximation leads to inevitable assumptions and/or simplifications. It is dependent on the extent it makes sense to the analyst
- Measurement errors
- Time, cost and resources availability impose a constraint on the analysis depth
- Uncertainty propagation. In a sequence of events, there is combined uncertainty deriving by the uncertainty of the involved variables
Annotated Bibliography
- C. R. Fox and G. Ülkümen, "Chapter 1: Distinguishing Two Dimensions of Uncertainty," in Perspectives on Thinking, Judging, and Decision Making, Oslo, Universitetsforlaget, 2011, pp. 22-28. This chapter explains in depth the theory for distinguishing between epistemic and aleatory uncertainty, giving research finding that support the distinctions.
- D. V. Lindley, "Uncertainty," in Understanding Uncertainty, New Jersey, John Wiley & Sons, Inc., 2006. The whole book provides a good general introduction regarding the role of uncertainty in everyday life. It provides simple examples for everyday situations explaining the logic of uncertainty behind them. The book does not get involved with complex mathematical concepts, however it provides the reader with good understanding of aspects of uncertainty.
- Handbook of Risk Theory: Epistemology, Decision Theory, Ethics, and Social Implications of Risk, New York, Springer, 2012. Uncertainty is closely related to risk management. This handbook provides an overview for several aspects or risk theory, addressing several ones relative to the decisions that a projects/program/portfolio manager may be called to make (e.g. decision theory, risk perception, ethics and social implications). It aims to promote communication and information among all those who are interested in theoretical issues concerning risk and uncertainty.
- T. Aven and E. Zio, "Some considerations on the treatment of uncertainties in risk assessment for practical decision making," Reliability Engineering & System Safety, vol. 96, no. 1, pp. 64-74, 2011. This research paper presents how to treat and quantify uncertainty in risk assessment, when it comes to using risk assessment for supporting decision making.
- K. Rui, Z. Qingyuan, Z. Zhiguo, E. Zio and L. Xiaoyang, "Measuring reliability under epistemic uncertainty: Review on non-probabilistic reliability metrics," Chinese Journal of Aeronautics, vol. 29, no. 3, pp. 571-579, 2016. In this journal paper, a review of non-probabilistic reliability metrics is conducted to assist the selection of appropriate reliability metrics to model the influence of epistemic uncertainty.
- Project Management Institute, Project Management: A guide to the project management body of knowledge (PMBOK guide) – Sixth Edition, Project Management Institute, 2017, pp. 68, 133, 177, 234, 397. This book provides processes and knowledge areas that comprise best practices in project management. In the pages mentioned, it introduces the ways that uncertainty enters project management aspects. It casts light on how uncertainty is perceived and how it affects project management.
- Project Management Institute, "Program and Project distinctions," in The standard for Program Management - Fourth Edition, Project Management Institute, 2017, pp. 28-29. The book is a guide for individuals and companies aiming to improve their program management, by providing good practices applicable to all programs. In the proposed section, it provides information regarding uncertainty in Programs, and gives details regarding the differences between uncertainty in programs and projects.
- Project Management Institute, "Portfolio Risk Management," in Portfolio Management: The standard for portfolio management, 4th Edition, Project Management Institute, 2018, pp. 86-92. The book is a guide for portfolio management. It deals with the discipline of doing the right work and provides up to date portfolio management practices. In the given pages, it presents how uncertainty affects portfolio management and how it is incorporated into managing the portfolio risk.
Relative wiki articles
- Risk management in project portfolios, link: Risk management in project portfolios
- Managing Uncertainty and Risk on the Project, link: Managing Uncertainty and Risk on the Project
- Risk management process, link: Risk management process
- Concept of Risk Quantification and Methods used in Project Management, link: Concept of Risk Quantification and Methods used in Project Management
References
- ↑ 1.0 1.1 , Management of Uncertainty - Theory and application in the design of systems and organizations, London: Springer, 2009.
- ↑ 2.0 2.1 2.2 A. D. Kiureghiana and O. Ditlevsen, "Aleatory or epistemic? Does it matter?," Structural Safety, vol. 31, no. 2, p. 105–112, March 2009.
- ↑ S. Basu, "Chapter 2: Evaluation of Hazard and Risk Analysis," in Plant Hazard Analysis and Safety Instrumentation Systems, London, Elsevier, 2017, p. 152.
- ↑ T. Aven and E. Zio, "Some considerations on the treatment of uncertainties in risk assessment for practical decision making," Reliability Engineering & System Safety, vol. 96, no. 1, pp. 64-74, 2011.
- ↑ 5.0 5.1 D. V. Lindley, "Uncertainty," in Understanding Uncertainty, New Jersey, John Wiley & Sons, Inc., 2006, pp. 1-2.
- ↑ 6.0 6.1 6.2 E. Zio and N. Pedroni, "Causes of uncertainty," in Uncertainty characterization in risk analysis for decision-making practice, number 2012-07 of the Cahiers de la Sécurité Industrielle, Toulouse, France, Foundation for an Industrial Safety Culture, 2012, pp. 8-9.
- ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 C. R. Fox and G. Ülkümen, "Chapter 1: Distinguishing Two Dimensions of Uncertainty," in Perspectives on Thinking, Judging, and Decision Making, Oslo, Universitetsforlaget, 2011, pp. 22-28.
- ↑ 8.0 8.1 8.2 8.3 8.4 Project Management Institute, Project Management: A guide to the project management body of knowledge (PMBOK guide) – Sixth Edition, Project Management Institute, 2017, pp. 68, 133, 177, 234, 397.
- ↑ Project Management Institute, "Program and Project distinctions," in The standard for Program Management - Fourth Edition, Project Management Institute, 2017, pp. 28-29.
- ↑ Project Management Institute, "Portfolio Risk Management," in Portfolio Management: The standard for portfolio management, 4th Edition, Project Management Institute, 2018, pp. 86-92.
- ↑ 11.0 11.1 N.-E. Sahlin, "Unreliable Probabilities, Paradoxes, and Epistemic Risks," in Handbook of Risk Theory, New York, Springer, 2012, pp. 492-493.
- ↑ C. J. Roy and W. L. Oberkampf, "A Complete Framework for Verification, Validation, and Uncertainty Quantification in Scientific Computing (Invited)," in 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, 2010.
- ↑ 13.0 13.1 K. Rui, Z. Qingyuan, Z. Zhiguo, E. Zio and L. Xiaoyang, "Measuring reliability under epistemic uncertainty: Review on non-probabilistic reliability metrics," Chinese Journal of Aeronautics, vol. 29, no. 3, pp. 571-579, 2016.
- ↑ 14.0 14.1 J. C. Helton and J. D. Johnson, "Quantification of margins and uncertainties: Alternative representations of epistemic uncertainty," Reliability Engineering and System Safety, vol. 96, no. 9, pp. 1034-1052, 2011.
- ↑ L. A. Zadeh, "Fuzzy sets as a basis for a theory of possibility," Fuzzy Sets and Systems, vol. 1, pp. 3-28, 1978.
- ↑ G. J. Klir, "Generalized information theory," Fuzzy Sets and Systems, vol. 40, pp. 127-142, 1991.