Internal rate of return (IRR)
The Internal Rate of Return (IRR) is a powerful discounted cash flow method used in capital budgeting and corporate finance to estimate and evaluate the profitability of potential investments. Keeping in mind the formula for the Net present value (NPV), the IRR is defined as the discount rate that makes the present value of the costs (negative cash flows) of an investment equal to the present value of the benefits (positive cash flows). In other words, the IRR is the discount rate that gives a net present value of zero when applied to the expected cash flow of a project. This rate of return is called internal because the formula predicts a rate that depends only on the project, more precisely on the project's cash flows, and does not depend on external factors such as market interest rates or inflation [1]. One of the main advantages in using the internal rate of return to evaluate project investments, compared to other methods such as the Payback period or the Benefit-cost ratio, is that IRR considers the time value of money[2]. In general, due to the relationship between NPV and IRR, the higher the Internal Rate of Return of a project, the more desirable the investment to be made. This article shows also the limitations of the internal rate of return; however, when the IRR is unique, it provides relevant information about the return on investment and is also used as a measure of investment efficiency. In fact, according to academic research [3], three-quarters of Chief Financial Officers (CFOs) use the IRR method to evaluate capital projects.
Contents |
Big Idea
Relevance of Internal Rate of Return
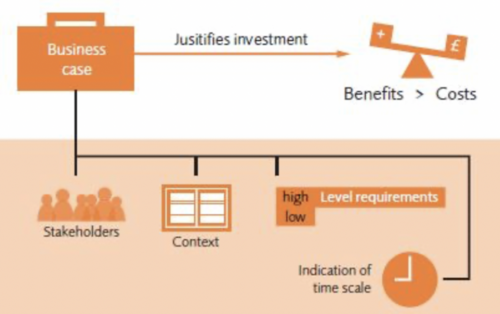
In a typical project lifecycle, there are some costs associated with running the project and, then, hopefully, there are some benefits that represents the value of doing the project. Are the associated costs worth the investment based on the potential future value generated? The management office often has to decide on whether or not to authorize investment in a project or among different projects options.
Effective project organizations focus their limited resources on the best projects, declining to do projects that are good but not good enough. The final decision depends on many factors such as the project feasibility, the costs, the probability to finish the project on time, the technical and commercial risks, the tangible and intangible benefits [5]. According to APM standard [4]: "the business case provides justification for undertaking a project programme or portfolio. It evaluates the benefit, cost and risk of alternative options and provides a rationale for the preferred solution".
The Project Management Institute (PMI) [6] defines the five primary steps for selecting, prioritizing, and coordinating projects to increase value to an organization. The focus of the third step is to select the best project according to the company criteria and there are two main approaches to define valuation criteria based on the consideration of the time value of money:
- Discounted methods
- Non-discounted methods
The difference between these two methods is the consideration of the monetary value of time, which is explained in detail in the next paragraph.
Time value of money
The first category listed above takes into account the time value of money. If it is needed to compare the cash flows available at different times, it is also needed to include the time value of money, which states that there is a difference between the future value and the present value of the same amount of money. So, to know the discounted cash flows of the project, therefore, it is necessary to discount the future cash flows through the discounting process. The reverse process, to be able to compare cash flows in the future, is called compounding [7]. In short, time is money hence having $ 100 today is different from having $ 100 tomorrow, and this paragraph explains why.
The monetary value of project investment is the value of the project's future cash flows (or net benefits) less the required investments (or initial costs). A key consideration regarding discounted cash flow methods is the Time Value of Money (TVM). In finance, an amount of money available today or in the future has a different value because we have to consider that also time has a monetary value. The reason is that today you have the opportunity to invest money and thus grow, according to the time horizon and the interest rate. Another reason for the time value of money is the purchasing power of money which changes over time due to inflation or deflation [8]. Hence, the time has a monetary value and we have to consider it if we want to compare money available in different moments. It is, therefore, necessary to briefly underline three fundamental terms about investments to clearly understand the time value of money:
- The Present value PV: the sum of money available today that can be invested [$];
- The Interest rate (or opportunity cost if we decide not to invest) r: the amount of interest due per period, as a proportion of the amount deposited or borrowed [%]
- The Future value FV: is the value of a current asset (present value) at a future date based on an assumed rate of growth (interest rate) [$].
| Present to Future (compounding) | 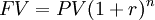
|
|---|---|
| Future to Present (discounting) | 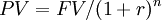
|
Example 1
Would you rather have $ 100,000 today or the same amount in 1 year from now?
To calculate how much money will be $ 100,000 in a year from now, supposing an interest rate r = 3%, we can apply the formula for the future value:
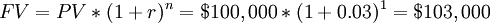
Having $ 100,000 now is equivalent to having $ 103,000 in the future considering an interest rate of 3%. If we agreed to receive $ 100,000 in one year instead of now, we would be $ 3,000 less. As shown, the present value and the future value differ by a factor of 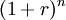 ; this difference represents the time value of money. It can be concluded that to compare the money available in two different moments it is necessary to consider the time value of money, which allows us to discount money available in the future and consider it in the present or vice versa; only then can we compare the two amounts.
; this difference represents the time value of money. It can be concluded that to compare the money available in two different moments it is necessary to consider the time value of money, which allows us to discount money available in the future and consider it in the present or vice versa; only then can we compare the two amounts.
Example 2
After an initial investment of $ 100,000 for machinery, the management expects an annual future cash flows of $ 40 000 for the next 4 years thinking to gain $ 60 000 (-100 000 + 40 000*3) at the end of the 4-year period. Is it true?
In finance, to calculate the profitability of a project considering future cash flows, it is needed to consider an alternative investment with almost the same risk to know the interest rate of the other investment. Considering an interest rate r = 7%, we can now calculate the time value of money because we have the interest rate. So,
| cash flow (0) | cash flow (1) | cash flow (2) | cash flow (3) | cash flow (4) | |
| Today | - 100,000 | ||||
| 1st year | + 40,000 | ||||
| 2nd year | + 40,000 | ||||
| 3rd year | + 40,000 | ||||
| 4th year | + 40,000 |
As described before, to compare money available at different times we have to make them available today, in other words, the discount of the time value of money applying the Preset Value formula:
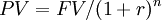
Hence, to obtain the table following table, we need to:
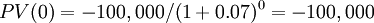 It is obvious to notice that the present value of a certain amount of money already available in the present is the same amount of money.
It is obvious to notice that the present value of a certain amount of money already available in the present is the same amount of money.
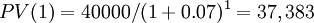
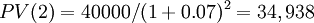
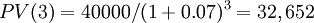
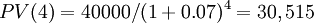
| cash flow (0) | cash flow (1) | cash flow (2) | cash flow (3) | cash flow (4) | Time value of money | |
| Today | - 100,000 | 0 | ||||
| 1st year | + $ 37,383 | + 40,000 | - $ 2,617 | |||
| 2nd year | + $ 34,938 | + 40,000 | - $ 5,062 | |||
| 3rd year | + $ 32,652 | + 40,000 | - $ 7,348 | |||
| 4th year | + $ 30,515 | + 40,000 | - $ 9,485 | |||
| Total cash flow (0) | = $ 35,488 | = - $ 24,512 |
We can suggest to the management that the investment is profitable because the total cash flow (0) (first column), or Net Present Value, is greater than zero ($ 35,488). However, it is lower than the expectation ($ 60,000) because of the time value of money. In fact, $ 60,000 - $ 24,512 = $ 35,488
From this example, it may be useful to note that:
- The Net Present Value is the present cash flow of the project and it is obtained by discounting the cash flows;
- The difference in value between future and present cash flows (time value of money) is inversely proportional to time and the interest rate. This means that the more a cash flow is in the future, the more its value will decrease if it is to be carried over into the present [9].
Understanding the Internal Rate of Return
A good understanding of the methodological basis of Net Present Value is required to truly comprehend the essence of the internal rate of return method, as it is closely related to NPV and allows management to add valuable information on decision criteria rather than just look at NPV.
Net Present Value
Net Present Value is a discounted cash flow method used to analyze the profitability of a project and is the difference between the present value of cash inflows and the present value of cash outflows over a period of time [10]. To calculate the NPV of a project with future cash flows, it is necessary to discount them considering the time value of money. The NPV is the sum of these discounted cash flows and reflects the profitability of the project [11].
Mathematically:
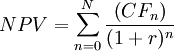
- n: current year
- N: time horizon
- CF (n): cash flow relative to n-year
- r: discount rate
The NPV of an investment project reflects in monetary terms the project profitability. Analyzing the formula for NPV it can be concluded that, according to the discount rate (r) considered in the formula:
- if NPV > 0: the discounted inflows are higher than the discounted outflows, hence the investment project will generate profit;
- if NPV < 0: the discounted inflows are lower than the discounted outflows, hence the investment project will generate loss;
- if NPV = 0: the discounted inflows are equal to the discounted outflows, hence the investment project will not generate profit or loss.
It is useful to observe that as the discount rate increases, the NPV decreases, and vice versa. Shortly, they are inversely proportional as shown by the graph above. [12]
Example
Suppose that management want to know the expected rate of return on their company's investment in the new project over the 5-year period. The investment consists of buying 10 new lathes for $ 50,000 each, supposing an annual inflow of $ 10,000 for the first, second and third year, $ 15,000 for the 4th and 5th years. How much profit (or loss) can this project generate? Consider three different discount rates: r1 = 11%, r2 = 6%, r3 = 5%.
Using the formula for NPV:
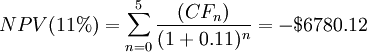
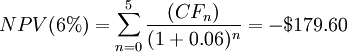
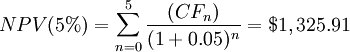
As expected, since the Net Present Value and the discount rate are inversely proportional, as one decreases, the other one increases. However, as shown by the example, as the discount rate changes, the value of the NPV also varies and therefore our decision to invest in the project can change.
The next paragraph is focused on the selection of the discount rate which is a crucial decision to decide if investing in a project or not, trying to answer these questions: what exactly is this rate? Are there any rules for determining the discount rate? How do I know if my decision is based on the correct discount rate?
Discount rate and WACC
The internal rate of return is the discount rate that makes the net present value equal to zero. Therefore, an introduction to the role of the discount rate and its influence on the decisions of companies regarding project investments is necessary.
A company decides to invest in a project only if the expected revenues exceed the expected costs; in short, if the project is profitable. In the "Time Value of Money" paragraph we saw the importance of time in discounted cash flow analysis; we have also seen that the difference between future value and present value is due to the time value of money and for this reason, $ 100 today is not $ 100 tomorrow. The discount rate makes it possible to have an estimate of the present value of the project's future cash flows in a discounted cash flow analysis because it reflects the time value of money [13]. As shown in the last paragraph, the discount rate plays a key role in discounted cash flow analysis and can make the difference between deciding to invest in a project or not.
Deciding which discount rate to apply in a project investment decision is an important point. There is not a single way to determine the discount rate, it depends on the company. Conventional management theory suggests to use the weighted average cost of capital (WACC) as the discount rate to decide investments on new projects [14]. In situations where the new project is considered riskier than normal business operations, the discount rate will be equal to the average cost of capital to which an additional percentage is added which corresponds to a risk premium because there is a risk that future cash flows will be lower than expected [15].
Looking at the NPV formula, it can be seen that the net present value and the discount rate are inversely proportional. The problem is that there is not a unique correct method to decide which discount rate to use in the formula, and by changing this rate in the calculation, the NPV also changes and consequently the investment decision also changes. It would be useful to have a specific discount rate that allows management to understand the threshold between investing and not investing in a project. In the next section, we discuss this useful discount rate and how management can make decisions quickly using it.
Application
IRR decision criteria
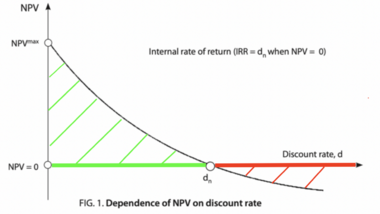
Looking at the graph of the relationship between the net present value and the discount rate, it can be seen that as the discount rate increases, the net present value decreases. And this is intuitive because:
- It is assumed that the discount rate is at least equal to the average cost of capital so that as the cost of capital increases, the profit will decrease;
- Mathematically, the discount rate is in the denominator and as it increases, the net present value decreases.
Furthermore, it can also be noticed that there is a particular discount rate, called the Internal Rate of Return, for which NPV is equal to zero and for each discount rate before the IRR, the net present value is higher than zero.
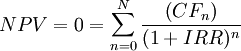
This is the reason why the IRR is an important method to use in evaluating a project because it allows the management to quickly understand with a single calculation which is the most convenient project. The higher is the IRR, the greater the amount exceeds the Weighted Average Cost of Capital (WACC) and the more net cash the project generates for the company (graphically, the NPV area is larger).
Example
Knowing that the cost of capital (WACC) is 10%, a company have to decide to invest in one of the following projects:
| Project A | Project B |
|---|---|
| - $ 5,500 | - $ 2,500 |
| $ 2,200 | $ 900 |
| $ 2,400 | $ 1,200 |
| $ 2,100 | $ 1,000 |
| $ 2,000 | $ 900 |
| $ 1,200 | $ 800 |
CONTINUE
- table insert 1st column years
- graph
- result on excel
Once the most convenient rate of return of the project has been identified, the NPV will be calculated to obtain a monetary value of the expected cash flow
Hence, considering the weighted average cost of capital (WACC) as the minimum rate of return, it can be concluded that:
- If WACC < IRR (NPV > 0)
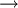 the project is attractive
the project is attractive
- If WACC > IRR (NPV < 0)
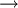 the project should be rejected;
the project should be rejected;
Because of the formula, the IRR is not easy to be calculated analytically and instead should be calculated iteratively or by using software, for example by Excel.
Example
Limitations
Multiple IRRs
The first limitation related to the internal rate of return is that sometimes this rate is not unique and this problem is called multiple internal rates of return [17]. It happens when the positive and negative cash flows are more than one. With multiple IRRs, the single IRR decision criteria rule is no longer valid. How can multiple IRRs be in accordance with the project cash flows? The answer is that the maximum number of IRRs obtained equals the number of sign changes in the project's cash flows. This is why this method is very useful in projects where there is an initial investment, followed only by positive cash flows, and not useful in projects with many positive and negative cash flows.
IRRs reinvested rate
The IRR reflects the profitability of a project, assuming that the profit of the project is reinvested at the same rate of profitability, which is the internal rate of return [17]. In practice occurs rarely because part of the profit is assigned to dividend, part is invested in another project that assumes less risk but at the same time is less profitable [16].
Overall size and scope of the project
The internal rate of return method only compares the cash flows to the initial capital spent to generate those cash flows, it does not take into account the size or scope of the project. If there are two projects that require very different levels of capital, the smaller projects tend to be overrated compared to the larger projects using the IRR calculation. For this reason, a company considers different metrics before making an investment [18]
Annotated bibliography
[continue...]
References
- ↑ BERNHARD, Richard H. Discount methods for expenditure evaluation-a clarification of their assumptions. The Journal of Industrial Engineering, 1962, 13.1: 19-27.
- ↑ Haight, Joel M.. (2012). Principles of Industrial Safety - 5.2.5 Net Present Worth. American Society of Safety Professionals
- ↑ John R. Graham and Campbell R. Harvey, “The theory and practice of corporate finance: Evidence from the field,” Duke University working paper presented at the 2001 annual meeting of the American Finance Association, New Orleans.
- ↑ 4.0 4.1 APM Body of Knowledge 7t, 3.1.1 Business Case
- ↑ Lock: Project Management (10th Edition)
- ↑ Project Management Institute, Inc. (PMI). (2021). A Guide to the Project Management Body of Knowledge (PMBOK ® Guide) – 7th Edition and The Standard for Project Management. Project Management Institute, Inc. (PMI)
- ↑ Torries, Thomas F.. (1998). Evaluating Mineral Projects - Applications and Misconceptions. Society for Mining, Metallurgy, and Exploration (SME)
- ↑ Runge, Ian Charles. (1998). Mining Economics and Strategy - 5. Time Value of Money. Society for Mining, Metallurgy, and Exploration (SME)
- ↑ Khatib, Hisham. (2014). Economic Evaluation of Projects in the Electricity Supply Industry (3rd Edition) - 5.3.3 Benefit/Cost Ratio. Institution of Engineering and Technology (The IET)
- ↑ Project Management: "Managing Successful Projects with PRINCE2" 6th Edition (2017)
- ↑ Mular, Andrew L. Halbe, Doug N. Barratt, Derek J.. (2002). Mineral Processing Plant Design, Practice, and Control Proceedings, Volumes 1-2 - 21.2.7 Sample Calculation of NPV and IRR. Society for Mining, Metallurgy, and Exploration (SME)
- ↑ Temizel, Cenk Tuna, Tayfun Oskay, Mehmet Melih Saputelli, Luigi A.. (2019). Formulas and Calculations for Petroleum Engineering - 7.28 Present Value of an Annuity. Elsevier
- ↑ Clar, Michael L. Traver, Robert G. Clark, Shirley E. Lucas, Shannon Lichten, Keith Ports, Michael A. Poretsky, Aaron. (2015). Low Impact Development Technology - Implementation and Economics - 6.6.4.3 Calculate Cost-Effectiveness. American Society of Civil Engineers (ASCE)
- ↑ Corporate Finance Institute. "WACC."
- ↑ CHRISTINA MAJASKI, CHARLENE RHINEHART, SUZANNE KVILHAUG (2022). Cost of Capital vs. Discount Rate: What's the Difference?
- ↑ 16.0 16.1 Mackevičius, Jonas ; Tomaševič, Vladislav. «Evaluation of investment projects in case of conflict between the internal rate of return and the net present value methods, 2010
- ↑ 17.0 17.1 Marko Miletic, Domagoj Latinac. Internal rate of return method - a commonly used method with few advantages and many disadvantages?
- ↑ Internal Rate of Return Method Advantages and Disadvantages, 1st October 2018, Brandon Gaille