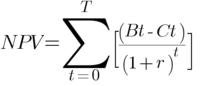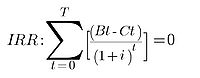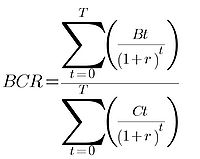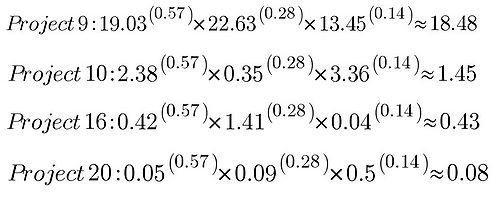Strategic Assessment: framework for combining CBA and MCDA

Developed by Giorgio Galasso - s212985

Risk management in portfolios, programs, and projects has the objective of setting goals and business objectives with the core vision and values of the organizations. Meanwhile, the formation of the Sustainable Development Goals (SDGs) and the required commitment from the organizations, has led to a formation of new core values and visions to be pursued. Consequently, the portfolio and project management process has developed significantly in the last years, portfolio managers must ensure that organizations competing in a dynamic and uncertain environment are aligned with their strategies , while program and project managers are responsible for implementing and successfully managing the different criteria generated by the external opportunities and threats. Yet, most of the assessments of projects belonging to portfolios and programs are limited on the application of the Cost-Benefit Analysis (CBA), mainly focusing on the profitability of projects. While the CBA provides a lot of insightful economic data (e.g., NPV, BCR, IRR), project assessments should consider also social and environmental criteria (e.g., economic development, public image, environmental sustainability) to strive for success. Therefore, the scope of the article is to set a framework for aiding the assessment process of program projects , through the combination of the traditional Cost-Benefit Analysis and the more recent Multi-Criteria Decision Analysis (MCDA), by providing a mix of tools which considers monetary goals, as also non-monetary strategic goals. This framework assumes that the pre-screening phase of the decision support system proposed by N.P. Archer and F. Ghasemzadeh has already been performed, and thus the set of criteria characterizing the program's projects have already been assessed.Moreover it will not provide an application example of the CBA, since the method is widely spread and used by most of the companies. Finally the article will consider the limitations of this framework, providing suggestions to mitigate the typical difficulties related to the tools, facilitating and aiding the decision-making process during risk assessments. In order to provide an effective and appliable tool for the reader, this article will focus on the application of the REMBRANDT technique during the MCDA phase, and then on the COSIMA approach, used to combine the results from CBA and MCDA.

Figure 1: Applicability of CBA and MCDA under different conditions .

Introduction

The purpose of quantitative risk analysis is to get a clear overview from a managerial perspective of which might be the uncertainties involved in a project, in order to estimate numerical, often monetary, values associated to each risk, which are usually considered costs. At the same time opportunities can be identified, and usually, once they are associated a value, they can be defined benefits. While in some cases quantitate risk assessments can not be conducted, and thus only a qualitative risk assessment can be executed, it is still essential to update the process of program/project risk assessment whenever it is necessary, in order to meet the requests of the many different stakeholders involved in the organizations. This framework can be used to evaluate which projects, independent between each other or not, should enter in a portfolio. Moreover, it can also be used to select which projects should enter a specific program whenever the resources are limited, and a selection has to be made. Yet, in the case of interdependent projects, as specified in the framework limitations, some adjustments should be made in order to aid the decision makers as much as possible With this purpose in mind, the article will be structured with an introduction on the CBA and MCDA methods, highlighting the values they provide, along with their limitations. Thereafter the application of REMBRANDT and COSIMA approaches will be explained in detail through Excel examples, after a theoretic background is provided. Finally, the limitations of this mix of tools/framework will be presented, followed by suggestions to avoid or mitigate the shortcomings exposed.

CBA

The Cost-Benefit Analysis became a popular tool in the 1960s and is mainly used for the risk assessment and appraisal of relevant projects, yet it can be used also for smaller projects. The aim of the CBA is to compare different projects considering both financial flows and economic impacts on the society, in a common and objective monetary metric . For example, a project involving railways construction, will not only consider the variation of the financial flows inside the organization, but also indirect impacts such as “Reduced time travel” and “Safety Increased”. As the financial flows and the economic flows are assessed, these are then confronted in order to measure the positive/negative impact on society’s welfare. One of the most important factors used in the CBA is the discount rate, which takes in account the assumption that benefits are more valuable in the present, rather than in the future. It is fundamental to not confuse the discount rate with the inflation rate. Thus, the value provide by a benefit decreases over time, and the costs will also decrease as the project goes on. There are many outputs once the CBA has been completed, the most relevant investment criteria for projects assessment are the following:

1. NPV:

The Net Present Value is an investment criteria utilized for determining whether or not a project will be profitable. It considers the difference between benefits (e.g, user impacts/benefits) and costs (investments cost, maintenance), discounted during all the period of the project. The requirement to fulfill the profitability condition for a project is NPV>0. When comparing projects, the ones with higher NPVs should be selected. A NPV-based selection is recommended whenever the program consists of projects that are dependent between each other, i.e., if the execution of a project excludes or limits the possible execution of a different project.

Figure 2: NPV formula

2. IRR:

The Internal Rate of Return determines the discount rate which balances costs and benefits of the project. The higher the discount rate determined, the higher the value of the project when compared between other projects in the same program.

Figure 3: IRR formula

3. BCR:

The Benefit-Cost Rate takes in account the rate between discounted benefits and discounted costs during the whole project duration. The requirement for a profitable project is to have a BCR>1. A BCR-based selection is recommended whenever the program consists of budget-constrained projects, which are also independent between each other.

Figure 4: BCR formula

In the suggested framework, the BCR, as well as the sum of the benefits and the costs, will be used as inputs during the COSIMA approach.

Limitations

The most important limitations regarding the CBA are the following:

1. Long term and strategic impacts:

Some impacts are impossible or very hard to assess, especially strategic impacts, e.g., decrease of stress among workers.

2. Discount rate:

The discount rate principle relies around the conception that a benefit is more valuable today rather than tomorrow, therefore privileging present generations instead of the future ones. This concept goes against many definitions of sustainability and it displays the need to update and combine the CBA with other assessment tools.

3. Unit prices determination:

The estimation of unit prices for non-marketable impacts, such as pollution reduction and safety improvements, may be quite difficult, leading to assumptions and more subjective-based unit prices. This problem can lead to misunderstandings and conflicts with the stakeholders involved in the project assessment, in fact the goal of the CBA is to provide an objective economic analysis.

4. Hypothetical results and uncertainty:

Even if the CBA makes estimations based on forecasts and the aggregated willingness to pay, there is no actual cash-flow, making the project appraisal process results debatable.

MCDA

Multi-criteria decision making has its roots in ancient times, with some raw early applications by characters like King Solomon, going to more recent times with Benjamin Franklin and with further developments during the 20th century, which led to the creation of many different theories and schools of thought.. In the last years, especially since the financial crisis of 2008, the involvement of stakeholders has become essential for the companies who strive for success, many organizations have already adopted an open-system mindset, trying to optimize the flow of resources with the external environment. Thus, when making the screening of projects for a portfolio or when comparing projects belonging to the same program, it has become necessary to utilize a Social Responsible Investment process (SRI), which considers also social, environmental and ethical criteria during the investment decision making. As in every decision support system there is the need to decompose the problem in smaller, so does each MCDA method. The first step is to determine the set of alternatives (pre-screening), secondly the alternatives' characteristics are defined through a set of criteria, and finally a preference structure for the decision makers is generated, by transforming preferences in weights. There are two main schools of MCDA, the French school and American school. The first one assumes that the decision makers don't have an ordered preference system, except for a preference in criteria, thus it focuses the outranking methods that can be used in the pre-screening phase. The American school assumes instead that the decision makers have already a preference system. The methods applied in this article are part of the American MCDA school. The most applied methods are the following:

1) The Simple Multi Attribute Rating Technique (SMART)

2) SMART Exploiting Ranks (SMARTER)

3) The Analytic Hierarchy Process (AHP)

4) Ratio Estimation in Magnitudes or deci-Bells to Rate Alternatives which are Non-DominaTed (REMBRANDT or Multiplicative AHP)

The MCDA technique used in this framework is the REMBRANDT, but independently from the chosen MCDA method, it is of extreme importance that the criteria chosen during the MCDA are not overlapping with the impacts measured in the CBA, since this would lead to double-counting errors during the composite analysis.

Limitations

As represented in Figure 1, the MCDA provides more value when considering strategic/political objectives, and it serves as a supplement to the CBA, yet some common weaknesses can be identified in the MCDA methods.

The most problematic MCDA limitations are the following::

1.Criteria Selection

It can happen that the decision makers find difficulties in determining the set of criteria on which to assess the projects. The criteria used in the pre-screening may be useful, but it may happen that these ones overlap entirely or partially with the impacts covered by the CBA. This would lead to an inaccurate and low-value analysis.

2.Time and resource intensive

Given the participatory nature of the activities to be performed during the MCDA, the amount of time and resources used during the appraisal of projects will increase considerably. Yet, there are some uplifts, since this is a way to improve the knowledge sharing inside an organization, moreover the analysis will be made considering the insights generated by different stakeholders, increasing the probability of effectiveness of the project.

3.Criteria weights

Arguably the most difficult step of the MCDA depending on many factors. There are many methods for eliciting weights, with many of them being too complex to being implemented in an environment with non-high-knowledge stakeholders. Making sure that everyone understands the importance of assigning weights and the functioning of the weighting process is fundamental in order to avoid potential conflicts and to increase the transparency of the whole assessment. There may be times where the recommended solution will not be the one hoped in the beginning.

Application

The application of this framework starts with a MCDA method, REMBRANDT, where the different projects will be evaluated basing on a set of criteria, then they will be weighted, providing the best performing alternative basing on the decision makers preferences. In order to ensure the quality of the process, also sensitivity and consistency analysis will be performed. After the results from the MCDA are available, those will be combined with the main outputs from the CBA, through the COSIMA approach. An alternative to COSIMA for combining CBA and MCDA is SIMDEC, but given that COSIMA is much more simpler to understand for the stakeholders, especially those who are acquainted with the CBA, the framework won't make use of the SIMDEC method.

REMBRANDT technique

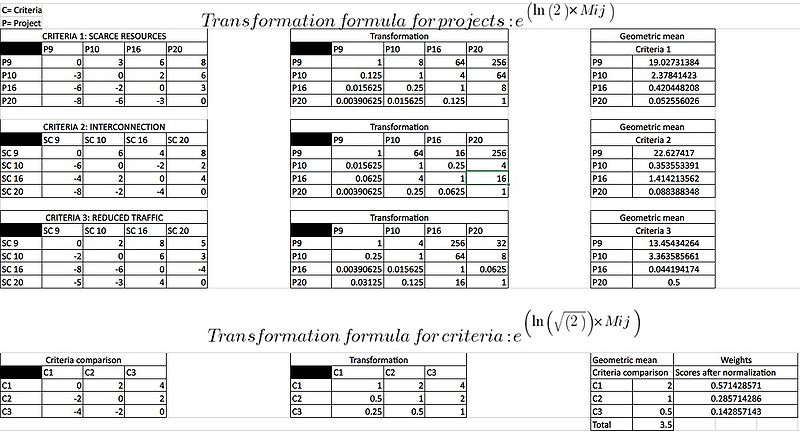
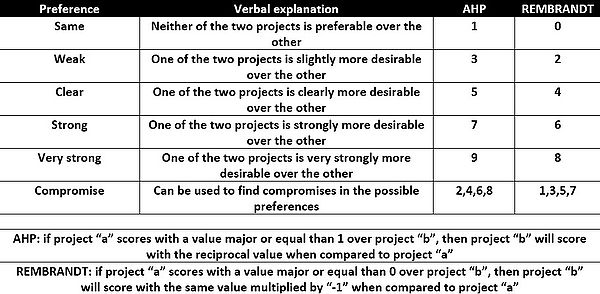
The origin of REMBRANDT sets in 1992, as a response to the critiques characterizing the AHP, in fact the two methods are very similar. The REMBRANDT, as the AHP, makes the decision makers assess the different alternatives/projects between each other on each criteria, making use of a numerical scale to translate verbal opinions into numbers. Once the scores for all the alternatives under each criteria are assessed, those will be transformed by using an exponential equation which considers a progression factor. Finally, the different projects for each criteria are given a value basing on the geometrical mean of their performances when compared to the other projects under the same criteria. The same process but with minor differences is repeated with the criteria, first they are assigned a score from the REMBRANDT scale, then transformed with a different progression factor, after which the geometrical mean for each criteria performance is calculated. Finally, the criteria performances will be normalized, providing the weights for determining which project is the most desirable. An example of calculations will be shown in Figure 6.1 and 6.2.

Figure 5: REMBRANDT and AHP scales

Steps

Criteria selection

A set of criteria on which performing the analysis is required, is possible to implement the same ones used in the pre-screening of the portfolio project selection, even the criteria which characterize the program can be chosen. Yet, as written before, it is fundamental to not choose criteria which take into account impacts already assessed in the CBA. Examples of possible criteria may be: Reduced Work Stress (if a program is characterized by projects related to the implementation of structural changes inside an organization) or Reduced Scarce Resources (if the program involves construction projects). As long as the set of criteria does not overlap with the CBA impacts, and as long as the criteria chosen are somehow measurable (otherwise it would be difficult to assess the project performances under each criteria), the set of criteria can be used in REMBRANDT.

Alternatives pair-wise comparisons and relative scores

Once a set of criteria has been decided, the alternatives are compared between each other by making use of the REMBRANDT scale for pair-wise comparisons (Figure 5). Once the comparisons are completed, the scores will be transformed by using the transformation formula in Figure 6, finally the alternatives' performances under each criteria will be scored through the use of the geometric mean method (geo. mean for each row).

Criteria pair-wise comparisons and weights determination

The process for making criteria pair-wise comparisons is the same as the one for alternative. The only exception consists in a different progression factor (square root of 2 instead of 2). After the values are transformed and the geometric mean is calculated, all the scores are summed in order to normalize each criteria score. The final normalized criteria scores correspond to the weights

Figure 6.1: REMBRANDT example on project comparison and criteria weight assessment, including the transformation formulas

Final scoring

The final scores are calculated by multiplicative aggregation. The performance of each project under each criteria is raised to the power of the corresponding criteria weight and multiplied with its weighted performances under all the other criteria. This process repeats for all the projects, providing a score for all the different projects, which can be normalized. An example of final scores calculation can be found in Figure 6.2, which continues the example introduced in Figure 6.1.

Figure 6.2: REMBRANDT example project final scores

Consistency analysis

Sometimes decisions and preferences, especially in the pair-wise comparisons, can generate inconsistencies, thus it is important to check if the matrixes generated during the REMBRANDT are consistent. In order to do so, the scores must be converted from the REMBRANDT to the AHP scale (Figure 5). Once the conversion has been completed, the largest eigenvalue of the matrix has to be found to calculate the Consistency Index (CI) and the Consistency Ratio (CR). The formulas can be found in Figure 7. A consistency ratio minor or equal to 0.1 is acceptable.

Figure 7: Consistency Index and Consistency Ratio formulas

Sensitivity analysis

A sensitivity analysis in recommended to assess under which conditions the suggested solutions shift. Therefore, it is necessary to change the value assigned to the set of criteria, (i.e., changing the preference system) and observe the consequences on the suggested solutions. There might be, especially when many criteria and projects, may different shifts in the solution, which can give some insight to the decision makers.

COSIMA approach

The principle of COSIMA (composite modelling assessment) is to incorporate the missing strategic criteria from the CBA, by incorporating the ones assessed during the MCDA. The application revolves around the concept that the final score when assessing the desirability of a project, the Total Rate of Return (TRR), which is the rate of the Total Value (TV) for each project and its costs. The TV is the sum of the value created by the CBA impacts and the value created by the MCDA criteria. In order to assign a monetary value to the MCDA benefits, a calibration factor (α) is introduced as a trade-off between CBA and MCDA. This factor can be explained easily to the decision makers as an MCDA%. An MCDA% of 0% will mean that all the benefits are credited to the CBA results, an MCDA% of 50% and CBA% of 50% will mean that the decision makers perceive CBA and MCDA equally valuable. Once the MCDA% has been determined, the project with highest BCR is selected for determining a set of prices. COSIMA relies on the assumption that the BCR is the best investment criteria, and thus if the MCDA should account as, for example, 50% of the value provided by the CBA, then the sum of all the benefits of that project is used as starting point for determining the shadow prices. In the following section an application of the method will clarify the process, while in Figure 8 can be found the TRR and TV formulas.

Figure 8: TV and TRR formulas

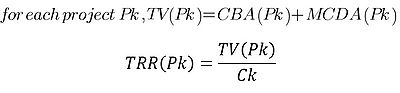
Steps

Inputs from CBA

The inputs required from the CBA application, are the sum of all the benefits, the sum of all the costs and the BCR. The benefits are needed to calculate both the Total Value and the shadow prices. The costs are needed to determine the Total Rate of Return. An example is shown in Figure 9.

Figure 9: CBA inputs for COSIMA

Inputs from REMBRANDT and value function scoring

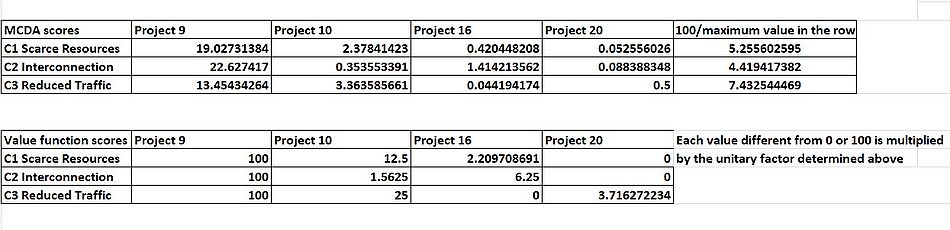
In this step it is necessary to transform the scores for each alternative under each criteria in value function scores. In order to do so, the highest scoring project under one criteria is assigned the value of 100, while the worst performing project is assigned the value of 0. The other values for the projects in between can be identified in many different ways. One way consists in dividing 100 by the score that the best performing project has under that criteria, obtaining the value needed to achieve the value 1 in the value function scale. Subsequently that value needs to be multiplied with the remaining REMBRANDT scores. An example which follows the values obtained by the MCDA example in Figures 6.1 and 6.2 is shown in Figure 10.1

Figure 10.1: Transformation from REMBRANDT scores to Value Function scores

MCDA% and calculation of shadow prices

Now that the value function scores have been assessed, the set of shadow prices must be calculated basing on the MCDA% chosen for the analysis. In order to apply the formulas, the CBA value to be considered, as mentioned before, is the sum of the benefits of the highest BCR project. Once the MCDA value has been calculated, the value function scores of the projects are multiplied with the price associated with each criteria. In order to pass from an equation with as many variables as the number of projects, to one that has only 1 variable, instead of using different prices for each criteria, the price will be the same for all the criteria, but each one will be weighted differently. Each price, other than the related value function score, will multiply the weight of the criteria obtained in REMBRANDT (Figure 6.1) corresponding to the value function score, divided by the weight of the criteria where the project performs better. Formulas and example calculations are in Figure 10.2.

Figure 10.2: Shadow-prices determination

Determination of the TRR

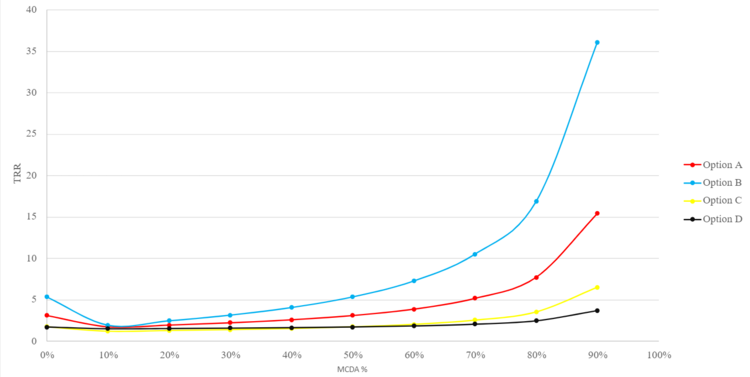
Now that the prices corresponding to the value provided on each criteria have been found, those have to be multiplied with the relative value function score for all the projects (Figure 10.2). The result of this multiplications is the MCDA value of each project under each criteria. When summed all together, the total MCDA value of the Project is determined. Finally, the projects TRRs are determined by the sum of the total CBA value and total MCDA value, divided by the total investment cost. As it is possible to see in Figure 10.3, the best performing project when considering an MCDA% of 50% is Project 9. The TRR expresses the desirability of a project basing on the decision makers preferences, and doesn't directly state which project will be the most valuable.

Figure 10.3: Projects TRRs

Comparison of the different projects/alternatives basing on the MCDA%

During the COSIMA analysis, the decision makers shouldn't start with a precise mindset on which balance to give between the CBA and the MCDA benefits. Instead, determining the TRRs considering all the possible percentages can generate many insights if the decision makers are unbiased. By changing these, desirability reversals between projects happen often, providing valuable conversations and different perspectives. The percentages to be considered should go from 0% (only CBA benefits) to 100% (only MCDA values) by a 10% factor. The range most interesting to analyse is usually between 30% and 70%. The results should be presented as a chart, in order to make the results analysis accessible to certain types of stakeholders. In Figure 11 a possible chart design is shown for 4 options, even if it is not correlated with the example shown above.

Figure 10.3: Projects TRRs

Framework's limitations

-The involvement of stakeholders in the MCDA can lead to many improvements for both the organization and the portfolio, program, and project risk assessment process, yet it requires many resources. Particularly, the pair-wise comparisons used in REMBRANDT can lead to many disagreements and much time spent. It is recommended the use of facilitation techniques for maintaining high the morale of all the decision makers.

-The use of COSIMA implies that the decision makers will have high consideration of the BCR during the assessment and the risk analysis process. In fact, the basic assumption of COSIMA is that the most desirable project from the CBA is determined by the highest BCR.

-The BCR is recommended for inter-independent project, which is not always the case, especially when evaluating projects in a program instead of a portfolio. Therefore, in the case of assessment of projects in the same program, during the COSIMA approach the choices regarding the best performing project should be made considering the NPV instead of the BCR. In fact, the NPV is recommended for projects with inter-dependencies in terms of resources.

-This framework doesn't consider which stakeholders should be involved during the process. With this regard, many stakeholder engagement techniques can be used to consider which people should be involved whenever needed.

-Some of the procedures during the application can be quite hard to understand for stakeholders with few practical knowledge of mathematics and finance practices. Communication about details regarding the most logically-difficult concepts, such as the alpha factor used in COSIMA, should be avoided to avoid perplexity. At the same time this way of action slightly decreases the transparency of the decision making process, from the point of view of those stakeholders. The way of tackling this problem mainly depends on which stakeholders are being engaged.

Annotated bibliography

1) Barfod, M. B., & Leleur, S. (Eds.) (2014). Multi-criteria decision analysis for use in transport decision making. (2 ed.) DTU Transport. Available at :https://backend.orbit.dtu.dk/ws/portalfiles/portal/104276012/DTU_Transport_Compendium_Part_2_MCDA_.pdf

This compendium illustrates in detail the main theories used to create this framework, including extra tools that can be used as substitutes in order to combine CBA and MCDA. It has been used as the main source of data for the article, under the approval of the author. The reading is suggested for those who want to get more knowledge on the other MCDA techniques mentioned in this article, as well as those who want to explore further weight elicitation techniques.

2) International Journal of Project Management Volume 17, Issue 4, August 1999, Pages 207-216, An integrated framework for project portfolio selection Authors, N.P Archer, F .Ghasemzadeh Available online 9 February 1999. Available at: https://www.sciencedirect.com/science/article/pii/S0263786398000325

This article provides an overview of the decision support process for the selection of project portfolios, proposing a decision support system and a project portfolio selection framework, it also suggest the utilization of an MCDA technique, the AHP, providing another perspective on the MCDA phase. If the decision support system and processes for selecting projects are still unclear to the reader, then this article is recommended.

3) Multiple Criteria Decision Making : Applications in Management and Engineering Edited by Constantin Zopounidis , Edited by Michael Doumpos. Available at https://www.bookdepository.com/Multiple-Criteria-Decision-Making-Constantin-Zopounidis/9783319818603?ref=bd_ser_1_1.

This book gives an overview of the multi-criteria decision making process, while also providing many MCDM case studies and applications.