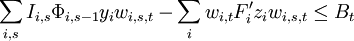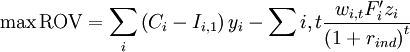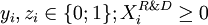Valuation methods in Project Portfolio Optimization - Focus on Real Options
Developed by Wilfried Genier
Contents |
Abstract
Valuation methods are critical supporting tools for any decision in Project Portfolio Management, so as to optimize the project portfolio in terms of expected return for the different values (e.g. money, knowledge, strategic alignment). This article quickly presents general valuation techniques for generic portfolio management (NPV, DCF, see below), but might be more relevant as applied to R&D portfolio selection and optimization.
A project portfolio is optimized by evaluating a multi-objective ranking based on (1) the expected return, (2) the uncertainty, and (3) the strategic fit, while optimizing several budgets allocation:
- Financial budget,
- Technological or knowledge-based budget,
- Budget based on the market uncertainty
- Critical resources allocation budget
R&D portfolios optimization is based on project valuation, and an alternative to classical, individual evaluation, methods such as NPV (Net Present Valuation) is the real options valuation.
The core principle is similar to the principle of financial options: holding a decision which is to be made is equivalent to have an option, which can be valued. The only difference is the materiality of the option (‘real’), as opposed to the abstract nature of a financial option.
The real option valuation is based on a mixed set of input data, balanced between the expected return, the expected consumed resources and the different risk factors.
Project Portfolio Optimization (PPO), in short
Key Highlights on Project Portfolio Management and Project Portfolio Optimization
Project Portfolio Management is the “bridge between strategy and operations”, as state Morris and Jamieson, [1] [2]. A successful Project Portfolio is therefore a portfolio that will have enabled the company to achieve a sustainable competitive advantage[3]. However, making this portfolio management and optimization is not an easy thing, as it presents several major difficulties :
- projects may have conflicts in their objective. Indeed objectives can be hard to compare, align or match, as some are tangible and others intangible[4]. Some objectives might also be contradictory.
- the uncertainties associated with project parameters, costs and risks make each comparison harder to make and each decision harder to take, as accurate forecasts are hard to achieve [5][6]. These strong interdependences are generally in the areas of limited resources consumption, risk balancing and strategy alignment.
- some projects are highly interdependent, with some projects benefiting to others, some project tying up resources for others, etc. Therefore considering the portfolio as a sum of singl projects is an inaccurate vision, potentially severely misleading. The portfolio has to be modelled as a whole [7]
A litterature review also shows that there are two main factors leading to a failure of a portfolio to contribute to the implementation of the chosen strategy. The first one is implementing too many projects, outreaching the capacities and abilities of the organization [8] [9] [10] [11] [12] [13] [14]. The second one is satisfying short-term exigencies at the expense of long-term perspective, which may compromise long-term success. Taking a decision and choosing a project implies to bound the necessary resources to this project, resources that may be critical or strategic resources. Making the 'go' decision for a project based only on short-term views, and without considering the associated opportunity costs, may lead to refuse a truly good opportunity or prospect which would appear later in the future, because of the lack of resources, as the necessary resources to pursue are being tied up in marginal undertakings [15] [16][17].
Selection and Prioritization of Projects in a Portfolio
The main criteria for selection and prioritization are[18][9] [5] [7] [12]:
- alignment with corporate strategy: corporate strategy must be reflected in the project composition or mix of the portfolio, as well as in the resource allocation to projects within the portfolio;
- maximizing the value, either financial, with metrics such as NPV or ROI, or broader, though weighted scored models for instance;
- balancing of the portfolio, particularly balancing risk and return, long and short terms benefits, time to completion.
Classical Valuation Methods, for single projects
[[File:ECV docPortfolioManagement.png|thumb|400px|Determination of ECV by Cooper, Edgett and Kleinschmidt[19]]
The classical methods for evaluating projects are often DCF-based (Discounted Cash Flow), such as the classical NPV (Net Present Value) formulas. The following metrics can also be used: the IRR (internal return rate), ROI (Return Over Investment), ECV (expected commercial value), EV (Earned Value).
The project NPV (Net Present Value) can be calculated very simply [20]:
Project NPV = PV of free cash flow in production phase - PV of investment cost
where PV stands for Present Value, and is calculated as follows:
-
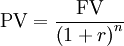 in discrete time, or
in discrete time, or
-
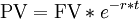 in continuous time,
in continuous time,
where FV is the future value of the cost (its estimate, or expectation), 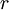 the discount rate,
the discount rate, 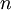 the number of (discrete) time periods between the future estimation and the present date, and
the number of (discrete) time periods between the future estimation and the present date, and 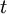 the amount of (continuous) time between the future estimation and the present date.
the amount of (continuous) time between the future estimation and the present date.
But these models can underrate some projects, particularly the riskier ones, in dynamic and fast-changing environment [6]
. Especially for R&D project portfolios, these methods might induce 2 main kinds of errors [6]
- Ignorance of the management flexibility, assumption of static cash flow. Does not take into account the possibility to interrupt a project to avoid more losses, for instance in case of technical failure (for instance tests failure, or other technical risks) or any economic risk, such as negative market variations. - Assumption that risk can only decrease the project value
Real Options for projects portfolios
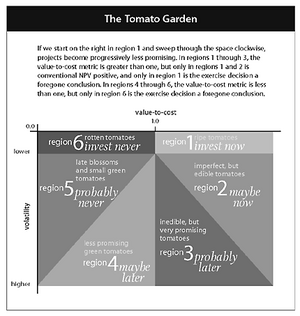
To explain how Real Options can prove useful in strategy and in portfolios, Luerhman [21] takes the metaphor of a tomato garden, with the gardener basically having the option to pick or not a tomato. This enables to describe the different kinds of options - see the picture 'The Tomato Garden' besides, and to describe the different behaviours that one can have. Whereas a passive gardener would merely walk and look in the garden, therefore only exercising his pick option or not-pick option, an active gardener would also monitor the tomatoes' evolution (thus monitor the options) and try to influence it in order to maximize his output from this garden.
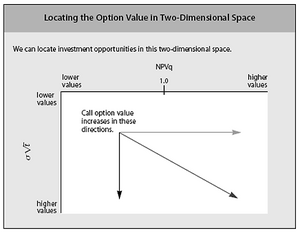
Luerhman offers two metrics for representing the options in a 2 dimensional options space. The first one is related to the output value, and is value-to-cost, defined as the ratio of the underlying assets intended to be built or acquired for the project over the present value of the expenditure required to build or acquire them. The second one is related to risks, and is a volatility metric (the cumulative volatility), defined by 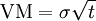 , where
, where  is the variance per period of asset returns, and
is the variance per period of asset returns, and  the time to expiration. Compared to the classical unidimensional representation, this bidimensional representation enables to differentiate more accurately among the options, and create the different regions shown on figure "The Tomato Garden", namely "now", "maybe now", "probably later", "maybe later", "probably never" and "never". Representing on a 2 dimensional space also gives more degrees of freedom in the possible movements, that is, more possibilities of action to move a project in a more interesting region. This representation can also be used for nested options, as illustrated in the example of Luerhman [21]
the time to expiration. Compared to the classical unidimensional representation, this bidimensional representation enables to differentiate more accurately among the options, and create the different regions shown on figure "The Tomato Garden", namely "now", "maybe now", "probably later", "maybe later", "probably never" and "never". Representing on a 2 dimensional space also gives more degrees of freedom in the possible movements, that is, more possibilities of action to move a project in a more interesting region. This representation can also be used for nested options, as illustrated in the example of Luerhman [21]
The aim of the real options approach for project selection in PPO is to ensure that the right projects are selected, with the right scope and at the right time, whereas the ‘not right enough’ projects are kept in nurturing until having reached their full potential to become a candidate for the portfolio value and entering the portfolio pipeline. (i.e. projects being in development) [22]
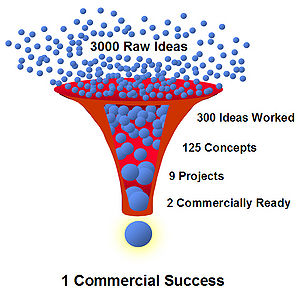
Real Options Valuation, a Simplified Model
From Financial Models to Real Options for Portfolio Management
The equivalence from Financial Options to Real Options is done through the translation of the input variables, according to the following table
| Input Variable | Financial option | Real option |
| S |
Underlying asset value |
Present value of the project expected incomes |
| X |
Exercise price |
Present value of the project investment costs |
| T |
Time to maturity |
Length of time in which the investment opportunity exists |
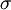
|
Volatility of returns on stock |
Volatility of project cash flows |
| r |
Riskless interest rate |
Riskless interest rate |
There are 5 main kinds of real options [6]
- Growth option, by adding new products or knowledge (R&D) to the portfolio or the project - Abandon option, which is the option to abandon at any stage of the project - Defer and wait, to reduce uncertainty - Contraction, meaning temporary or permanently suspending - Switch or transition option, for instance changing the product mix (output mix), or the resource mix (input mix)
Generally, the decision to put a research project in a portfolio can be considered as a growth option, which is equivalent to a financial call option [6] . The necessary input values can be selected as follows, based on the work of Merck mentioned in Enea, G. & Lo Nigro, G. (2011) [6]
- Underlying asset value: expected present value of the cash flows deriving from the commercialization of equivalent products - Exercise price: investment cost at the launch of the project (for instance facilities investment, patent exploitation licenses cost, start-up cost) - Time to expiration: expected completion time of the project - Volatility: for instance, standard deviation of the annual revenues for the concerned industry
This kind of option can be modelled in a closed form, with the Black & Scholes formula for instance [6]
. As mentioned previously, it is important to consider a research portfolio, and more generally a projects portfolio, as a whole and not only as a collection of individual projects, as there may be interdependencies. Therefore, the modelling of a portfolio is more likely to be done through a compound option, whose value can be estimated with a Geske model. A stochastic optimization model called OptFolio has been developed by Roger & Al [24]and simplified by Enea, G. & Lo Nigro, G. (2011) [6] into a model called OptFolio Light, which is presented below. The OptFolio maximizes the overall Real Options Value (ROV) of the portfolio, aiming at identifying the most valuable projects among the whole R&D projects portfolio of a company. It therefore can be used to select the best candidates from a set of R&D projects, those to be injected into the portfolio pipeline. In the original OptFolio, each R&D project process is modelled as a sequence of continuation/abandon (“go/kill”), with these decisions being taken at the beginning of each development phase of the project. Therefore, this is equivalent to financial Bermuda options, which are potions that can only be exercised on predetermined dates. In order to reduce the complexity of the model in OptFolio Light, Enea, G. & Lo Nigro, G. modelled the R&D process as a growth option instead of abandon, or as a sequence of growth options, depending on the number of development phases in the project. The simplified model also assumes that if a project is interrupted at any phase, it is dismissed from the optimal portfolio.
The Model OptFolio Light
Sets and variables
- Product:
![i \in [\![1;P]\!]](/images/math/1/8/9/189c5abe5aacca80568436dc3df0aabf.png)
- Stage of project development:
![s \in [\![1;S]\!]](/images/math/c/8/5/c8501309e598537833e2c2e252383ae5.png)
- Date, within the maximum time horizon T:
![t \in [\![1;T]\!]](/images/math/5/2/e/52ed75ac7448452a9b90df582f538b31.png)
Parameters
-
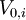 = current value of project
= current value of project  (at
(at 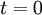 )
)
-
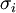 = estimated market volatility for project
= estimated market volatility for project 
-
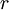 = risk-free interest rate
= risk-free interest rate
-
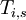 = length of stage
= length of stage 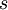 for project
for project 
-
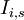 = investment cost of stage
= investment cost of stage 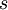 for project
for project 
-
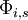 = probability of technical success of stage
= probability of technical success of stage 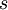 for project
for project 
-
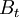 = budget constraint at date
= budget constraint at date 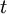 (for instance if the time scale is in year,
(for instance if the time scale is in year, 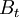 is the budget for year
is the budget for year 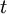 )
)
-
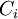 = real options value of project
= real options value of project 
-
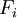 = annual cash flow brought by project
= annual cash flow brought by project 
-
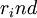 = rate of return in the concerned industry
= rate of return in the concerned industry
-
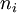 = expected duration of commercialization of the output of the project
= expected duration of commercialization of the output of the project 
-
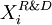 = percentage of cash flows of project
= percentage of cash flows of project  invested in R&D
invested in R&D
-
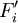 = amount of annual cash flow of project
= amount of annual cash flow of project  invested in R&D
invested in R&D
The real option value of project  can be calculated accordingly to the number of development stages [6]
can be calculated accordingly to the number of development stages [6]
| Number of development stages | Corresponding formula | |
| 1 stage of development |
Simple investment decision, therefore: |
|
| 2 stages of development |
Black and Scholes formula: where:
| |
| 3 stages of development |
Traditional Geske formula (see [25]) | |
| 4 or more stages |
Extended Geske model, developed by Cassimon & Al ([26]) |
The value of the uniform cashflow 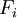 resulting from project
resulting from project  during
during  years is calculated with:
years is calculated with:
-
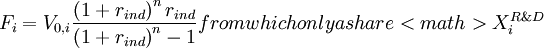 is reinvested in R&D, therefore:
is reinvested in R&D, therefore:
-
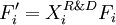
Decision variables
-
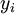 , binary variable which is equal to 1 if the project
, binary variable which is equal to 1 if the project  is selected in the portfolio, 0 otherwise;
is selected in the portfolio, 0 otherwise;
-
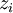 , binary variable which is equal to 1 if part of the cashflow of the project
, binary variable which is equal to 1 if part of the cashflow of the project  is reinvested in R&D, 0 otherwise; therefore we have a natural constraint
is reinvested in R&D, 0 otherwise; therefore we have a natural constraint 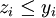 appearing, by definition of the variables.
appearing, by definition of the variables.
-
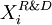 , a continuous variable belonging [0;1] and representing the percentage of cash flows of project
, a continuous variable belonging [0;1] and representing the percentage of cash flows of project  invested in R&D. identically, by definition, we have
invested in R&D. identically, by definition, we have 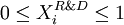
One more constraint is needed, the budget allocation one:
Complete Model
Finally, the complete OptFolio Light model formulation is:
s.t.
Note on indexing: there is a lag between the decision and its effect, therefore decision in present time (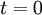 ) will influence the first development stage (
) will influence the first development stage (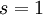 ), and identically for the following decisions and stages.
), and identically for the following decisions and stages.
Extensions
- Fuzzy models
- Sensivity analysis (directly reference the two articles on sensivity analysis)
Vocabulary (wip)
(wip) opportunity cost (wip)
Annotated Bibliography
Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE A thesis based on a case study in Vietnam, giving a good overview on Project Portfolio management goals, methods and techniques.
Enea, G. & Lo Nigro, G. (2011), A Real Options Based Model To Select a Balanced R&D Portfolio, University of Palermo and Geske, R. (1979); The Valuation of Compound Options. Journal of Financial Economics 7 (1979) 63-81. The two main documents of work for mathematical aspects.
Strategy as Portfolio of Real Options, Luehrman
Kodukula P., Papudesu, C. (2006) Project Valuation Using Real Options: A Practitioner's Guide, J. Ross Publishing
== References ==
[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][24][25][26]
- ↑ 1.0 1.1 Morris, P. & Jamieson, A. (2004). Translating Corporate Strategy into Project Strategy: Realizing Corporate Strategy through Project Management. USA: PMI. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 2.0 2.1 Dey, P. K. (2006). Integrated Project Evaluation and Selection Using Multiple- Attribute Decision-Making Technique. International Journal of Production Economics, 103 (1), 90-103. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 3.0 3.1 Dietrich, P. & Lehtonen, P. (2005). Successful Management of Strategic Intensions through Multiple Projects - Reflections from Empirical Study. International Journal of Project Management, 23 (5), 386-391. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 4.0 4.1 Ghasemzadeh, F. & Archer, N. P. (2000). Project Portfolio Selection through Decision Support. Decision Support Systems, 29 (1), 73-88. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 5.0 5.1 5.2 Radulescu, Z. & Radulescu, M. (2001). ‘Project Portfolio Selection Models and Decision Support’, Research Paper, National Institute for Research & Development in Informatics, Romania Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 Enea, G. & Lo Nigro, G. (2011), A Real Options Based Model To Select a Balanced R&D Portfolio, University of Palermo
- ↑ 7.0 7.1 7.2 Ghasemzadeh, F.; Archer, N. and Iyogun, P. (1999). A Zero-One Model for Project Portfolio Selection and Scheduling. The Journal of the Operational Research Society, 50 (7), 745-755. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 8.0 8.1 Wheelwright, S. C. & Clark, K. B. (1992). Creating Project Plans to Focus Product Development. Harvard Business Review, 70 (2), 70-82. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 9.0 9.1 9.2 Archer, N.P. and Ghasemzadeh, F. (1999). An Integrated Framework for Project Portfolio Selection. International Journal of Project Management, 17 (4), 207-216. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 10.0 10.1 Englund, R. L. & Graham, R. J. (1999). From Experience: Linking Projects to Strategy. Journal of Production and Innovation Management, 16 (1), 52-64. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 11.0 11.1 Cooper, R. G., Edgett, S. J., & Kleinschmidt, E. J. (2000). New Problems, New Solutions: Making Portfolio Management More Effective. Research Technology Management, 43 (2), 18-33. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 12.0 12.1 12.2 Yelin, K. C. (2005). Linking Strategy and Project Portfolio Management. In Levine, H. A. (eds.) (2005) Project Portfolio Management: A practical guide to selecting projects, managing portfolios and maximizing benefit, pp. 137- 145. USA: Pfeiffer Wiley. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 13.0 13.1 Crawford, L.; Hobbs, B. & Turner, J.R. (2006). Aligning Capability with Strategy: Categorizing Projects to Do the Right Projects and to Do Them Right. Project Management Journal, 37 (2), 38-50. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 14.0 14.1 Blichfeldt, B. S. & Eskerod, P. (2007). Project Portfolio Management - There’s More to It than What Management Enacts. International Journal of Project Management, in press, corrected proof. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 15.0 15.1 Frame, J. D. (1994). Selecting Projects that Will Lead to Success. Reprinted in: Dye, L. D. & Pennypacker, J. S. (eds). (1999) Project Portfolio Management: Selecting and Prioritizing Projects for Competitive Advantage, pp.169-181, Critical point is resource allocation, as finite resource available. Therefore, crucial to wisely allocate resources, especially strategic ones, to support the corporate strategy.
- ↑ 16.0 16.1 Porter, M. E. (1985). Competitive Advantage. New York, USA: The Free Press. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 17.0 17.1 Johnson, G., Scholes, K. & Whittington, R. (2006). ‘Exploring Corporate Strategy’. 7th ed. Harlow, Essex: Pearson Education Limited. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 18.0 18.1 Sommer, R. J. (1999). Portfolio Management for Projects: A New Paradigm. In Dye, L.D. and Pennypacker, J.S. (eds.) (1999) Project Portfolio Management: Selecting and Prioritizing Projects for Competitive Advantage, pp. 55-60. West Chester, PA: Center for Business Practices. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ 19.0 19.1 Cooper, R. G., Edgett, S. J. & Kleinschmidt, J. E. (2002) Portfolio Management: Fundamental for New Product Success, Stage-Gate, a copy is accessible here: http://www.stage-gate.net/downloads/working_papers/wp_12.pdf (last access September 24th, 2016)
- ↑ 20.0 20.1 Kodukula P., Papudesu, C. (2006) Project Valuation Using Real Options: A Practitioner's Guide, J. Ross Publishing
- ↑ 21.0 21.1 21.2 Luerhman, T. Strategy as a Portfolio of Real Options, via Schwarz, E. & Trigeorgis, L. (2001) Real Options and Investments Under Uncertainty, Classical Readings and Recent contributions
- ↑ Gardiner, P. D and Carden, J. (2004). The “Benefit Pipeline” Approach to the Strategic Implementation of Projects. IRNOP VI Conference, Turku, Finland. Via Cao Le, M. & Tau Nguyen, V. (2007), Strategy for Project Portfolio Selection in Private Corportations in Vietnam, Master Thesis USBE
- ↑ [1]
- ↑ 24.0 24.1 Rogers, M. J., Gupta, Maranas, C. D. (2002); Real options based analysis of optimal pharmaceutical research and development portfolios Ind. Eng. Chem. Res. 2002, 41, 6607-6620 Via Enea, G. & Lo Nigro, G. (2011), A Real Options Based Model To Select a Balanced R&D Portfolio, University of Palermo
- ↑ 25.0 25.1 Geske, R. (1979); The Valuation of Compound Options. Journal of Financial Economics 7 (1979) 63-81.
- ↑ 26.0 26.1 Cassimon, D, Engelen, P. J., Thomassen, L., Van Wouwe, M. (2004); The valuation of a NDA using a 6-fold compound option. Research Policy 33: 41–51 Via Enea, G. & Lo Nigro, G. (2011), A Real Options Based Model To Select a Balanced R&D Portfolio, University of Palermo
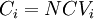
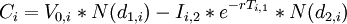
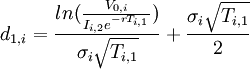
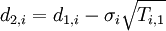
 is the cumulative normal distribution function
is the cumulative normal distribution function