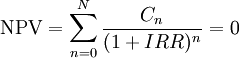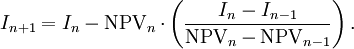Internal Rate of Return (IRR)
Developed by Pablo Leandro Capellari- s213666
Internal rate of return (IRR) is a parameter used in the financial analysis to determine the profitability of the investment, that is, it estimates the rate of return that the evaluated project could have. The term "internal" is because for the calculation of the IRR, external factors that could affect the profitability of the project, such as inflation, are not considered. In mathematical terms, the IRR is defined as the discount rate that causes the sum of the cash flows of the project to be zero[1]. In other words, if the Net Present Value (NPV) of a project is 0 at a certain rate, that rate is the IRR[2]. Researchers in 2003[3] have validated the IRR as an alternative to the NPV as an indicator for project evaluation, considering that the IRR as from the point of view of the investor and the NPV from the point of view of the society. This article aims to conceptualize the IRR in theoretical and mathematical terms with understandable contents, to be understood and used by project managers with different backgrounds. In addition, the most important uses of the IRR are described with practical examples. Finally, some of the limitations most highlighted by the literature are described.
Contents |
BIG IDEA
It is possible to consider a successful investment as one that manages to reach or exceed the expected returns, and investors tend to analyze how this type of investment has behaved in the past to have a vision of what could happen in the future. It is clear that past performance is not a guarantee of what might happen in the future, but it is an important influence on financial attractiveness. If the cash flow turns out to be as predicted, that the asset was valued rationally, the investor gets the expected rate of return. On the other hand, if the return is higher than expected, the actual return will be higher than the target rate. Therefore, different types of rates can be defined: a) the required rate of return: which is the target rate measured at the beginning of the investment, b) the real rate of return: which is the rate measured at the end of the project. In the market, both rates are known as IRR.[2]
The popular application of the IRR is mainly because it defines the return on investment, sometimes seen as a measure of efficiency, beyond its documented limitations. For decision-makers, the IRR can be compared to the discount rate for rejecting or accepting projects. To be specific, for a project to be accepted, the IRR must be greater than the discount rate and when both are equivalent, a situation of indifference arises[1]. To resolve many deficiencies related to the traditional IRR, some researchers[4] have proposed to use the average internal rate of return (AIRR). The AIRR is based on the breakdown of the NPV of the project between the invested capital and the economic efficiency, maintaining the consistency of the NPV to decide the acceptance of a project. This breakdown generates valuable information helping to determine the uncertainty of a project allowing risk to be explored in more detail.
General usage of IRR
As mentioned earlier, the IRR is an investment decision-making tool used to determine the viability of various investment options. The general criteria to understand the suitability of a project are the following:
- if TIR > r
 project is accepted. The reason for this is that the project generates a higher rate of return than the required minimum rate of return (opportunity cost), which means we will make more money than investing in a specific project (IRR), for example, buying government bonds.
project is accepted. The reason for this is that the project generates a higher rate of return than the required minimum rate of return (opportunity cost), which means we will make more money than investing in a specific project (IRR), for example, buying government bonds.
- If TIR < r
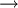 project will be rejected. The reason is that the project's return is lower than the required minimum return. This shows that if we invest in government bonds, we will make more money than if we invest in specific projects (IRR).
project will be rejected. The reason is that the project's return is lower than the required minimum return. This shows that if we invest in government bonds, we will make more money than if we invest in specific projects (IRR).
- If TIR = r
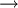 it would be a situation of indifference, similar to the one that occurs when the NPV is equal to zero.
it would be a situation of indifference, similar to the one that occurs when the NPV is equal to zero.
r= discount rate
The discount rate (r) is an approach of stating the rate of interest on an investment, which calculates the rate as the interest earned, divided by the future value of the investment.[5] This can be thought of as the rate of return that investors expect to earn when they provide capital at risk. Although each investor has her ideal rate of return, what matters is the collective number determined by the return expectations of millions of equity investors. [6]
IRR Mathematically
IRR is the discount rate (interest rate) that makes the sum of the present value of the cash flows zero. If the NPV of the project is zero at the selected discount rate, then that discount rate is, by definition, the IRR. IRR is algebraically equivalent. Mathematically expressed as[2]:
where 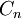 is a cash flow in period
is a cash flow in period 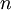
Numerical solution
Another alternative to calculating the 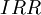 is the secant method:
is the secant method:
where 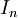 is considered the
is considered the 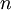 th approximation of the IRR.
th approximation of the IRR.
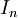 can be calculated with different levels of precision, for example, using the default functions in Microsoft Excel and Google Sheets. The convergence behavior is described by the following: "=IRR(...)" and "=XIRR(...)"
can be calculated with different levels of precision, for example, using the default functions in Microsoft Excel and Google Sheets. The convergence behavior is described by the following: "=IRR(...)" and "=XIRR(...)"
The convergence behaviour of by the following:
- If the function
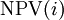 has a single real number root
has a single real number root 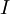 , then the sequence converges reproducibly towards
, then the sequence converges reproducibly towards 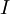 .
.
- If the function
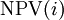 has
has 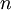 real roots
real roots 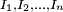 , In this case, the sequence converges to one of the roots, and changing the initial values can change the root to which the sequence converges.
, In this case, the sequence converges to one of the roots, and changing the initial values can change the root to which the sequence converges.
- If function
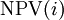 has no real roots, then the sequence tends towards +∞.
has no real roots, then the sequence tends towards +∞.
Having 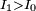 when
when 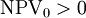 or
or 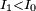 when
when 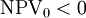 may speed up convergence of
may speed up convergence of 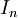 to
to 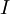 .
.
Practical example
In the following example, a highway construction project is outlined to demonstrate the calculation of IRR and other parameters. For exemplification purposes, the following data have been used: The project opens in year 0 and has an evaluation period of 10 years, the project has the following first-year impacts:
–Time savings: 500,000 DKK.
–Accident savings: 50,000 DKK.
–Operation and maintenance: 100,000 DKK.
| Discount rate | 0,03 |
|---|---|
| Traffic growth | 0,015 |
| Price growth | 0,01 |
In addition, different reference values have been used for this type of project, such as a discount rate of 3%, annual traffic growth of 1,5% and price growth of 1%.
| Year | - | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Discount factor | - | 1,09 | 1,06 | 1,03 | 1,00 | 0,97 | 0,94 | 0,92 | 0,89 | 0,86 | 0,84 | 0,81 | 0,79 | 0,77 | 0,74 |
| Traffic growth | - | 0 | 0 | 0 | 1,00 | 1,02 | 1,03 | 1,05 | 1,06 | 1,08 | 1,09 | 1,11 | 1,13 | 1,14 | 1,16 |
| Price growth | - | 0 | 0 | 0 | 1,00 | 1,01 | 1,02 | 1,03 | 1,04 | 1,05 | 1,06 | 1,07 | 1,08 | 1,09 | 1,10 |
| Construction costs | ,-10.612.090 | -3.642.423 | -3.536.333 | -3.433.333 | |||||||||||
| Scrap value | 7.440.939 | ||||||||||||||
| Operation and maintenance | -953.020 | - | - | - | -100.000 | -97.087 | -94.260 | -91.514 | -88.849 | -86.261 | -83.748 | -81.309 | -78.941 | -76.642 | -74.409 |
| Time savings | 5.372.322 | - | - | - | 500.000 | 497.646 | 495.302 | 492.970 | 490.649 | 488.338 | 486.039 | 483.750 | 481.473 | 479.205 | 476.949 |
| Accidents | 476.510 | - | - | - | 50.000 | 48.544 | 47.130 | 45.757 | 44.424 | 43.130 | 41.874 | 40.655 | 39.470 | 38.321 | 37.205 |
| NPV | 1.724.661 | ||||||||||||||
| BCR | 1,16 | ||||||||||||||
| IRR | 4,57% | ||||||||||||||
| (Simple example of the calculation of the IRR. Developed by Pablo Capellari s213666. | |||||||||||||||
The table displays year-over-year cash flows, plus calculations for Residual Value, Net Present Value (NPV), Benefit-Cost Rate (BCR), and Internal Rate of Return (IRR). For the calculation of the IRR, the Excel function "Goal Seek" has been used, where it allows estimating the IRR generating an NPV=0. Another option that can be used to calculate the IRR is the =IRR(cash flows) function in Excel.
Negative IRRs
In simple terms, a negative IRR indicates that the cash flows of a project are not enough to cover the initial investment. Therefore, this means that the project is not attractive to the investor. In such situations, the NPV would also be negative. On the other hand, a negative NPV value does not always mean a negative IRR, it just means that the discount rate is greater than the IRR.[7]
The following simple example allows us to clarify the concept of negative IRR.
| Year | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| Cash Flow | .-300.000,00 kr. | 30.000,00 kr. | 35.000,00 kr. | 50.000,00 kr. | 80.000,00 kr. |
| IRR | .-13% | ||||
| (Simple example of the calculation of a negative IRR. Developed by Pablo Capellari s213666. | |||||
The sum of the cash flows is negative, so it generates a negative IRR, in this case, the initial investment is 300.000,00 kr (Danish kroner) and the income in the four-year period adds up to a total of 195.000,00 kr (Danish kroner), for so the IRR is -13%.
APPLICATION
IRR for project managers
Risk Assessment in portfolios, programs and projects has the objective of defining the action patterns of an organization respecting its vision and values. Therefore, in recent years, risk analysis for the proper management of portfolios and projects has been evolving according to the dynamics and needs of the market, as well as the company's internal strategies. The vast majority of project risk assessments are limited to Cost-Benefit Analysis (CBA), numerically determining economic data (NPV, BCR, IRR). It is important to note that when evaluating a project it is essential to consider social and environmental criteria (economic development, public image, environmental sustainability), for example with the use of Multi-Criteria Decision Analysis (MCDA).[8]
The purpose of Cost-Benefit Analysis (CBA) is to compare different projects considering both financial flows and economic impacts on society, in a common and objective monetary metric. CBA can be used in projects of all scales, from large projects such as public infrastructure to smaller projects of a private nature. Public policy has many goals, affects different groups of beneficiaries, and spans different time horizons. The advantage of the cost-benefit analysis method is to simplify the multidimensionality of the problem by calculating the monetary value of each key benefit and cost. To make these elements fully comparable, the method converts all economic and financial flows observed at different times into current values. This method, called discounting, is essential for cost-benefit analysis. This allows projects to be evaluated according to how much society values the well-being of future generations. The idea is that benefits or costs are more valuable when they have a direct impact. Consequently, activities that result in high costs or benefits to future generations appear to be less important. The key here is to weigh the time period with an appropriate discount factor.[9]
The CBA can be elaborated under different methodologies, as well as the great variety of results that it is possible to obtain from it. The most relevant investment criteria are NPV, IRR and BCR. Net present value (NPV) considers the difference between benefits (impacts users and other benefits) and costs (investment and maintenance costs), discounted over the entire duration of the project. The criterion used to determine the profitability of the project is NPV>0, and when comparing projects, the project with the highest NPV should be chosen according to this criterion. It is clear that there are many factors involved in this decision, so the NPV should not be the only factor to consider. Therefore, the IRR also participates, since it determines the discount rate which balances costs and benefits of the project, which serves as a complement to the NPV criterion in the CBA. This is the main reason why the IRR is a tool for project managers at the time of project evaluation. Another important criterion in the CBA is the Benefit-Cost Rate (BCR), which considers the ratio between the discounted benefits and the discounted costs throughout the duration of the project. The use of the BCR is recommended for budget-constrained projects, which are also independent of each other. And the selection criteria for a profitable project is to have BCR>1. [8]
IRR in real-estate investment
It is a common opinion that the Internal Rate of Return (IRR) may be the real estate industry's preferred performance measure as a means of evaluating the return on projected investments. However, finance textbooks[10] pointed out that the net present value (NPV) is a superior method to the IRR used to evaluate potential investments, however, in practice, the internal rate of return still dominates. This is an easy-to-understand indicator that the appeal is that it meets the need for a single number compared to other opportunities or benchmarks. This simplicity belies its true nature and many of the problems that can arise when it is used to evaluate capital investment projects.[2]
IRR limitations on real state investments
- Does not express a measure of the size or timing of the project.
- Does not differentiate between sales revenues or cash flows from operations.
- Does not demonstrate the timing of cash flows.
- Assume cash flows can be reinvested.
- Does not differentiate risk levels between years within the project.
- No express leverage risk.
- Not influenced by real estate, lease, operating or liquidity risk.
IRR vs NPV for project ranking
In situations where it is necessary to choose between mutually exclusive projects, it can usually happen that there are differences in the results of the analyzes between the NPV and the IRR, which often causes problems for decision-makers. The use of the IRR is disputed for various reasons, but it is still widely used in practice [11]. The IRR tends to express the return on invested capital, a project should be accepted if the IRR is greater than the interest rate, because this case would generate a positive NPV [12]. This means that for these situations both indicators are consistent and the acceptance of a single project would be facilitated. For mutually exclusive projects, where these indicators rank in a different order than the alternatives, it is usually explained by the "investment assumption", which establishes that the differences between intermediate cash flows must be recognized. For these situations, the investor must consider what will happen to the differences in cash flows in between. For example, if project A has an initial investment of 200,000 kr (Danish kroner) and another project B an initial investment of 150,000 kr (Danish kroner), the decision-maker must consider what happens with that difference of 50,000 kr (Danish kroner). It is assumed that in this example, the NPV calculation is higher in project B, while the IRR is higher in project A. Therefore, the investor will have uncertainty between both projects, depending on whether to rely on the criterion of NPV or IRR. This author [11]proposes the use of the Investment Difference (DI), by which it is intended to compare the cash flows of mutually exclusive projects.
LIMITATIONS
The IRR is generally used by decision makers to choose which of the investment alternatives is the most attractive, unfortunately this rate has several defects:
Mutually Exclusive Projects
This limitation is related to the "IRR vs NPV for project ranking" section because if it is the only indicator used, this could cause erroneous decisions when choosing a project. This type of problem arises when the projects have different values of initial investment, let's suppose project A with an initial investment of 10,000 kr, an NPV of 80,000 kr, and an IRR of 100%. On the other hand, a project B with an initial investment of 100,000 kr, an NPV of 360,000 kr, and an IRR of 50%. Considering the IRR criterion alone, the investor could decide on project A (IRR=100%), but project B (IRR=50%) would generate 280,000 kr more. It is to be expected that in a project with higher investment, the profits are also higher. The analysis would be to invest 10 times in project A with the same investment used for project B, of course, if this were feasible. From another point of view, focusing the analysis on the NPV over the IRR would generate discarding the most profitable in percentage terms. A practical alternative to solve this situation from different perspectives is normalizing both projects, that is, dividing the cash flow of project B 10 times.[13]
The reason this approach fails is that any returns, viewed in isolation, do not account for wealth creation. There is no further information on the magnitude of the internal interest rate alone, so the fact that the magnitude of one internal rate is greater than the other indicates that the corresponding net investment [=invested capital] has a smaller magnitude. No other economic impact [14]. To provide information about the wealth created, a standardized rate of return that allows for expansion is required. However, the IRR method cannot provide such an index[15].
Multiple IRRs
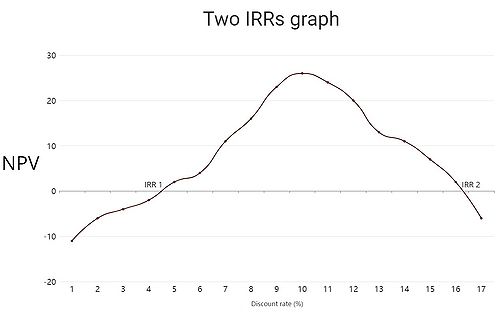
Generally speaking, projects start with a negative cash flow, which then turns into a series of positive cash flows. For example, in the case of real estate investments, the cash flow starts negative due to the purchase of the property and over the years it becomes positive due to the income from rentals or eventual sales. This typical situation generates a change in the "direction" of the cash flows, it generates a unique IRR. But in many other projects, this change of "direction" occurs repeatedly due to negative and positive cash flows being produced alternately, this effect generates what is commonly known as multiple IRRs. To continue with the example of real estate investments, this could be the situation where it is invested in some improvements to the property which generates negative cash flows.[2]
The use of the IRR is popularly accepted for single IRR projects, because this rate clearly defines the return on an investment, being a measure of project efficiency. However, these assumptions must be carefully considered in projects with multiple IRRs.
The graph on the right represents a project with two IRRs, the first (IRR1) of 4.7% and the second (IRR2) of 16.4%. The net present value (NPV) is represented on the vertical axis and the discount rate (%) on the horizontal axis.
Another common situation where multiple IRRs are obtained in investments with removal/remediation costs, phased expansion, natural resource extraction [16]. The multiple IRR problem can also be encountered when evaluating the ex-post economic performance for an ongoing activity (such as a company or business unit) over a given time interval if dividends and new investments alternate. In these situations, the main problem is the uncertainty of having multiple IRRs because it is not possible to give any of them a clear role[15].
IRR Incalculable
The impossibility of calculating the IRR is one of the most important criticisms of this indicator. One of the situations where this problem occurs is in projects where all cash flows are positive, which rarely happens in practice (it implies output, without input). Another situation where the IRR is not calculable is when all cash flows are negative. It is clear that in these two situations there is no doubt whether the project should be accepted or rejected. The third circumstance where IRR cannot be calculated is when net cash flow is zero.[13]
Hazen (2003)[14] proposes to correct the error by considering the real part of complex-valued intermediate capital. Although complex interest rates can confer economic importance [17], the attractiveness of real interest rates in practical applications is overwhelming, suggesting that there is an urgent need for a method that consistently provides a reliable value for real interest rate returns. As infrequently as there is in real life without IRR projects, when this happens, the consequences are devastating. Even theoretical paradigms that do not guarantee the existence of real returns should be questioned [15].
Reinvestment
This limitation of the IRR is based on the "investment assumption", and this is because the IRR assumes that the positive flows generated by the project are reinvested at the IRR, not at the discount rate. And the negative flows should divest the project but these are not considered to simplify the calculation. To correct inconsistencies arising from the use of implicit assumptions, simply make them explicit. For example, if it is necessary to know what the internal rate of return of the reinvested cash flow is at the discount rate, do the calculation twice. The second time, enter the actual cash flow generated by reinvested funds for all projects. If funds are available to pay off the debt, the avoided interest is included in the project's positive cash flow. Of course, it is essential to treat all projects equally in this regard if meaningful comparisons are to be made. While this technique would have been cumbersome when writing some of the most popular textbooks decades ago, modern electronic tools make it easy. However, this adjustment is usually unnecessary. In general, reinvesting at the IRR is a reasonable assumption. This is done in the matter of bond yields, which is ultimately an investment decision.[13][15]
Concocted capital
Researchers often interpret internal value (sometimes referred to as the "project balance sheet") as the capital invested in the project [14][18][19]. Just a special case where capital is assumed to grow at a constant rate of return each period. However, this assumption is often wrong, so internal capital does not represent the capital used by the project: they do not correspond to the economic resources used by investors and have no identifiable economic reference to market value, book value, or estimated capital, or any other intermediate value pattern, hence, intrinsic value is fictitious [20]. As such, IRR can be viewed (at best) as a cyclical return that is repeatedly applied to a patchwork of temporary capital that misrepresents real capital[15].
Changes in capital
Economically, the same cash flow vector may result from different economic policies, resulting in diverse capital investments and different returns. The empirical feature of the two projects is that dissimilar economic activities lead to different invested capital and returns: a reasonable return approach should recognize this variance, while the internal rate of return forces the two projects to share nominal capital despite empirical evidence. As a result, these two different projects are merged into the same asset, resulting in the same return. Despite the same cash flows, the projects are economically distinct: they are based on separate operations, with a distinct magnitude and distribution of income and interim capital. The IRR approach cancels out any economic distinction between the two projects, despite their different invested capital, income, and period return rates. Employing the IRR approach is to ignore the fact that, while wealth creation depends on cash flows, the rate of return depends on capital [15].
ANNOTATED BIBLIOGRAPHY
Hartman Joseph and Ingrid Schafrick. The relevant internal rate of return. 2004 [1]
This article clearly defines the IRR theoretically and mathematically, what is more, it presents a method to determine the acceptability of projects with multiple IRRs. During the development of the method, the authors explain the limitations of having several IRRs in a project.
Magni, Carlo Alberto. Average Internal Rate of Return and Investment Decisions: A New Perspective. 2010 [7]
This work offers a solution to the limitation generated by the IRR in project ranking when used in conjunction with the NPV, changing the usual perspective where the IRR does not depend on the cash flow but rather on the capital invested, that is, it allows the calculation of a rate of return in the relationship between income and capital.
Magni, Carlo Alberto. The Internal Rate of Return Approach and the AIRR Paradigm: A Refutation and a Corroboration. 2013 [15]
This paper shows that the Internal Rate of Return (IRR) method is unreliable and that the recently introduced Average Internal Rate of Return (AIRR) model provides the basis for an alternative theoretical paradigm of the rate of return. To this end, the authors divide the work into two parts: pars destruens and pars contruens. In the "disruptive" section, they present a summary of 18 shortcomings associated with the IRR approach. In the "constructive" part, they construct alternatives from four (independent) economic intuitions, and test the paradigm by showing that the paradigm has no previously examined shortcomings. It also shows how IRR is included in the new method as a rate of return.
Patrick Michael and Nick French. The internal rate of return (IRR): projections, benchmarks and pitfalls. 2016 [2]
This paper discusses the use of the IRR as the main measure of return on investments considering the weaknesses of the indicator. More specifically, it details the limitations of the IRR in capital budgeting decisions, highlighting why the IRR as an isolated reference can generate misleading results to evaluate investment alternatives. In addition, the IRR is defined mathematically.
References
- ↑ 1.0 1.1 1.2 Hartman, Joseph C., and Ingrid C. Schafrick. «THE RELEVANT INTERNAL RATE OF RETURN». The Engineering Economist, Vol. 49, no. 2, January 2004, p. 139-58. DOI.org (Crossref), External link.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Patrick, Michael, and Nick French. «The internal rate of return (IRR): projections, benchmarks and pitfalls». Journal of Property Investment & Finance, vol. 34, no. 6, January 2016, p. 664-69. Emerald Insight, External link.
- ↑ Tang, S.L., and H. John Tang. «TECHNICAL NOTE: THE VARIABLE FINANCIAL INDICATOR IRR AND THE CONSTANT ECONOMIC INDICATOR NPV». The Engineering Economist, Vol. 48, no. 1, January 2003, p. 69-78. DOI.org (Crossref), External link.
- ↑ Hazen, Gordon, and Carlo Alberto Magni. «Average Internal Rate of Return for Risky Projects». The Engineering Economist, Vol. 66, no. 2, April 2021, p. 90-120. DOI.org (Crossref), External link.
- ↑ Tintle, Nathan, et al. A spiral approach to financial mathematics. Academic Press, an imprint of Elsevier, 2018. External link
- ↑ Curto, Francesco. Valuing and investing in equities: cash return on capital investment (croci). 1.a ed., Academic Press is an imprint of Elsevier, 2020 External link.
- ↑ 7.0 7.1 Magni, Carlo Alberto. «Average Internal Rate of Return and Investment Decisions: A New Perspective». The Engineering Economist, vol. 55, n.o 2, mayo de 2010, pp. 150-80. DOI.org (Crossref), External link.
- ↑ 8.0 8.1 Barfod, M. B., and Leleur, S. Multi-criteria decision analysis for use in transport decision making. (2 ed.) DTU Transport, 2014. External link
- ↑ Le Maux, Benoît; Josselin, Jean-Michel. Cost Benefit Analysis, Statistical Tools for Program Evaluation — 2017, pp. 291-324 External link.
- ↑ Brown, Gerald R., and George A. Matysiak. Real Estate Investment: A Capital Market Approach. Financial Times Prentice Hall, 2000. External link
- ↑ 11.0 11.1 Kalhoefer, Christian. «Ranking of mutually exclusive investment projects – how cash flow differences can solve the ranking problem». Investment Management and Financial Innovations, Volume 7, Issue 2, 2010 External link
- ↑ Shapiro, A.C. «Capital Budgeting and Investment Analysis, Upper Saddle River, 2005 External link
- ↑ 13.0 13.1 13.2 Ray, Martin. TRIPOD: Internal Rate of Return Revisited External link. Retreived on 19 February 2022
- ↑ 14.0 14.1 14.2 Hazen, Gordon B. «A NEW PERSPECTIVE ON MULTIPLE INTERNAL RATES OF RETURN». The Engineering Economist, vol. 48, n.o 1, enero de 2003, pp. 31-51. DOI.org (Crossref), External link.
- ↑ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 Magni, Carlo Alberto. «The Internal Rate of Return Approach and the AIRR Paradigm: A Refutation and a Corroboration». The Engineering Economist, vol. 58, n.o 2, abril de 2013, pp. 73-111. DOI.org (Crossref), External link.
- ↑ Hartman, Joseph C. Engineering economy and the decision-making process. Pearson/Prentice Hall, 2007.External link
- ↑ Pierru, Axel. «The Simple Meaning of Complex Rates of Return». The Engineering Economist, vol. 55, n.o 2, mayo de 2010, pp. 105-17. DOI.org (Crossref), External link
- ↑ Crean, Michael. «Point of View Revealing the True Meaning of the IRR via Profiling the IRR and Defining the ERR». Journal of Real Estate Portfolio Management, vol. 11, n.o 3, enero de 2005, pp. 323-30. DOI.org (Crossref), External link.
- ↑ Blank, Leland T., y Anthony J. Tarquin. Engineering economy. 7th ed, McGraw-Hill, 2012 External link.
- ↑ Altshuler, Dean, y Carlo Alberto Magni. «Why IRR Is Not the Rate of Return for Your Investment: Introducing AIRR to the Real Estate Community». SSRN Electronic Journal, 2011. DOI.org (Crossref), External link